偏微分

偏微分とは？（やり方）

偏微分とは、多変数関数において一つの変数だけに関して行う微分です。（それ以外の変数は定数とみなします）

上記は２変数関数の場合の例ですが、３変数関数以上であっても同様に１つの変数に注目して微分を行います。

このページでは動画や下のような動かせる３Ｄグラフなどを使って、偏微分の図形的な意味や定義について視覚的に分かりやすく解説します。

その後、例題でいくつか偏微分の計算をやってみます。

図形的な意味

「多変数関数」のページで見れますが、３変数以上の関数になると視覚的に捉えることが難しくなります。

ここでは２変数関数の場合で説明します。

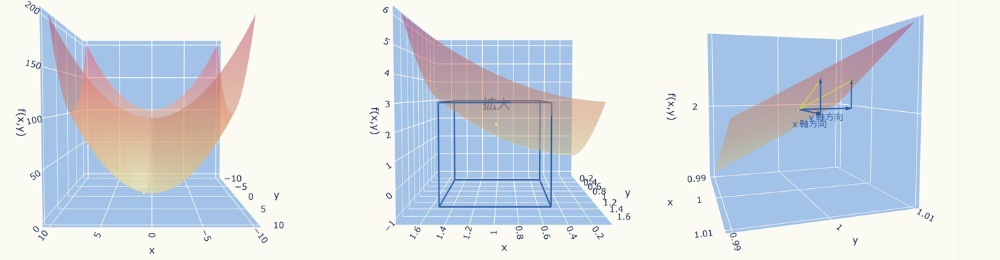
「微分の基礎」のページにおいて１変数関数のグラフを拡大すると直線になりましたが、２変数関数は拡大すると平面になります。

偏微分の図形的な意味としては、グラフを平面になるまで拡大した時の、軸方向の傾き（変化率）を求めることです。

なぜ偏微分の図形的な解釈がこのようになるかについては、「定義式の解釈」をご覧ください。

また、拡大すると平面になる理由に興味のある方は「拡大すると平面になる理由」をご覧ください。

ちなみに、これは\( \hspace{10pt} \displaystyle f(x,y) = x^{2} + y ^{2} \)の\( (x,y)=(1,1) \)付近を\( \pm 0.01 \)まで拡大したグラフです。

この程度の拡大でも、ほぼ平面になっていることが分かります。

偏微分記号

偏微分には複数の表記方法があります。

例えば関数\( f(x,y) \)の場合、次のような表記方法があります。

• \( x \)に関する偏微分

\( \hspace{10pt} \displaystyle f_{x}(x,y) = \frac{\partial f}{\partial x} = D_{x}f \)

• \( y \)に関する偏微分

\( \hspace{10pt} \displaystyle f_{y}(x,y) = \frac{\partial f}{\partial y} = D_{y}f \)

ちなみに、\( \partial \)は「ラウンド」と読みます。

定義

関数\( f(x,y) \)の偏微分の定義は以下となります。

スマホでご覧の方へ。式が画面からはみ出る場合はスクロールできます。

・\( x \)に関する偏微分
$$ \hspace{10pt} \displaystyle \frac{\partial f(x,y)}{\partial x} =    \lim_{\Delta x \to 0} \frac{f(x+\Delta x ,y) – f(x,y)}{\Delta x} $$
・\( y \)に関する偏微分
$$ \hspace{10pt} \displaystyle \frac{\partial f(x,y)}{\partial y} =  \lim_{\Delta y \to 0} \frac{f(x ,y+\Delta y) – f(x,y)}{\Delta y} $$

定義式の解釈

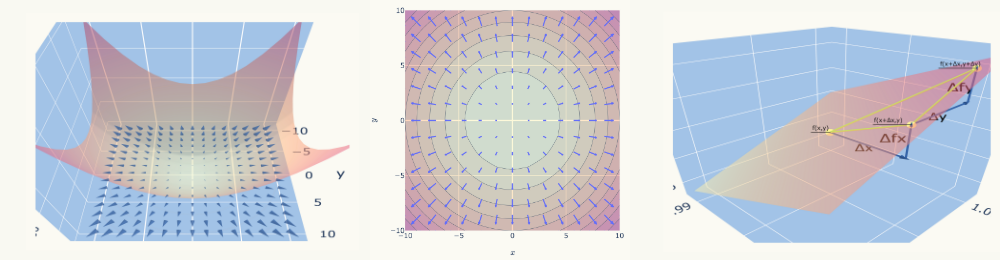
上記の「\( x \)に関する偏微分」の定義の右辺、\( \displaystyle \frac{f(x+\Delta x ,y) – f(x,y)}{\Delta x} \)の部分をグラフ化すると次になります。

分子の\( \displaystyle f(x+\Delta x ,y) – f(x,y) \)は\( y \)を変化させず、\( x \)を\( \Delta x \)だけ変化させた場合の\( f \)の変化量です。

つまり、\( y \)が一定のライン上で\( x \)軸方向に\( \Delta x \)だけ変化させた時の\( f \)の変化量です。

ここでは、例として\( y = 1.0 \)にしてグラフ化してますので、そのライン上での\( f \)の変化量になっています。

このグラフはドラッグで回転できますので、よければ回転させて\( y = 1.0 \)ライン上になっているか見てみてくださいね。

この分子を\( \Delta x \)で割った\( \displaystyle  \frac{f(x+\Delta x ,y) – f(x,y)}{\Delta x} \)は\( x \)軸方向に\( \Delta x \)だけ変化させた時の\( f \)の変化率（傾き）です。

動画で見たように、これが\( x \)に関する偏微分の基本的な考え方です。

定義式は単にこれを\( \lim_{\Delta x \to 0}  \)として\( \Delta x \)を限りなくゼロに近づけたものです。

小さな\( \Delta x \)を使えば、コンピュータ等を使った数値計算で偏微分の近似値は出ます。

しかし、理論値を得たければ定義式のように\( \lim_{\Delta x \to 0}  \)として、数式で偏微分を計算する必要があります。

定義式を使った偏微分計算

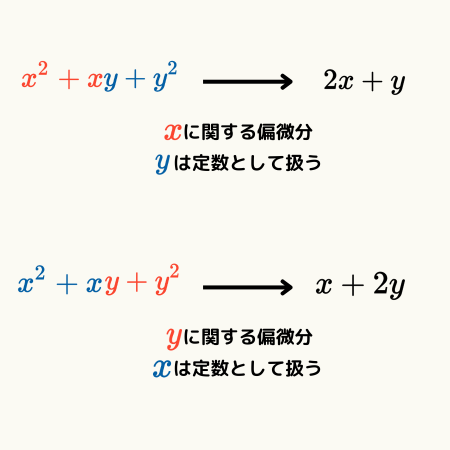
定義式を使って、\( f(x,y) = x^{2} + xy +y^{2} \)を\( x \)に関して偏微分してみます。

\( \hspace{10pt} \displaystyle \frac{\partial f(x,y)}{\partial x} =    \lim_{\Delta x \to 0} \frac{f(x+\Delta x ,y) – f(x,y)}{\Delta x} \)

\( \hspace{20pt} \displaystyle =    \lim_{\Delta x \to 0} \frac{1}{\Delta x} \left[ \left\{ (x+\Delta x)^{2} + (x+\Delta x)y + y^{2} \right\} – \left\{ x^{2} + xy +y^{2} \right\} \right]\)

\( \hspace{20pt} \displaystyle =    \lim_{\Delta x \to 0} \frac{1}{\Delta x} \left[ 2 \Delta x \hspace{1pt} x + \Delta x^{2} + \Delta x \hspace{1pt} y \right]\)

\( \hspace{20pt} \displaystyle =    \lim_{\Delta x \to 0}  \left[ 2 x + \Delta x + y \right]\)

\( \hspace{20pt} \displaystyle =     2 x + y \)

定義式上、\( y \)は変化させないため定数と同等となり、最初に述べたように計算結果は\( y \)を定数として扱って、\( x \)について微分したものとなります。

3変数以上の関数の場合

3変数以上の関数の偏微分の定義は、次になります。

\( n \)変数の関数\( f(x_{1},x_{2}, \cdots ,x_{n}) \)を変数\( x_{i} \)に関して偏微分する場合、
$$ \hspace{10pt} \displaystyle \frac{\partial f(x_{1},x_{2}, \cdots ,x_{n})}{\partial x_{i}} =    \lim_{\Delta x_{i} \to 0} \frac{f(x_{1},x_{2}, \cdots ,x_{i}+\Delta x_{i}, \cdots ,x_{n}) – f(x_{1},x_{2}, \cdots ,x_{i}, \cdots ,x_{n})}{\Delta x_{i}} $$

2変数の時と同様に１つの変数に注目して微分を行います。

拡大すると平面になる理由

この項目は大学レベルの数学の知識を使用します。
興味のある方はご覧いただければと思います。
飛ばして「例題」に進んでいただいても問題ありません。

2変数関数のテイラー展開は次式のようになります。

\( \hspace{10pt} \displaystyle f(x+\Delta x, y+\Delta y) = f(x,y) +\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \)

\( \hspace{50pt} \displaystyle + \frac{1}{2!} \left\{ \frac{\partial^{2} f}{\partial x^{2}}(\Delta x)^{2} + 2 \frac{\partial^{2} f}{\partial x \partial y}(\Delta x)(\Delta y) + \frac{\partial^{2} f}{\partial y^{2}}(\Delta y)^{2} \right\} \)

\( \hspace{50pt} \displaystyle + \frac{1}{3!} \left\{ \frac{\partial^{3} f}{\partial x^{3}}(\Delta x)^{3} + 3 \frac{\partial^{3} f}{\partial x^{2} \partial y}(\Delta x)^{2}(\Delta y) + 3 \frac{\partial^{3} f}{\partial x \partial y^{2}}(\Delta x)(\Delta y)^{2} + \frac{\partial^{3} f}{\partial y^{3}}(\Delta y)^{3} \right\} \)

\( \hspace{50pt} \displaystyle + \cdots \)

\( f(x,y) \)を左辺に移行して、関数の変化分\( \Delta f \)とすると、

\( \hspace{10pt} \displaystyle \Delta f = f(x+\Delta x, y+\Delta y) – f(x,y) \)

\( \hspace{25pt} \displaystyle = \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \)

\( \hspace{50pt} \displaystyle + \frac{1}{2!} \left\{ \frac{\partial^{2} f}{\partial x^{2}}(\Delta x)^{2} + 2 \frac{\partial^{2} f}{\partial x \partial y}(\Delta x)(\Delta y) + \frac{\partial^{2} f}{\partial y^{2}}(\Delta y)^{2} \right\} \)

\( \hspace{50pt} \displaystyle + \frac{1}{3!} \left\{ \frac{\partial^{3} f}{\partial x^{3}}(\Delta x)^{3} + 3 \frac{\partial^{3} f}{\partial x^{2} \partial y}(\Delta x)^{2}(\Delta y) + 3 \frac{\partial^{3} f}{\partial x \partial y^{2}}(\Delta x)(\Delta y)^{2} + \frac{\partial^{3} f}{\partial y^{3}}(\Delta y)^{3} \right\} \)

\( \hspace{50pt} \displaystyle + \cdots \)

\( \Delta x \)や\( \Delta y \)が微小な値の場合、2段目以降は無視できるようになるため、

\( \hspace{10pt} \displaystyle \Delta f = \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \)

のように変数が\( \Delta x, \Delta y \)の一次式になります。

これを少し変形すると、次式になり、

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \hspace{3pt} – \hspace{1pt} \Delta f = 0 \)

これは変数が\( \Delta x, \Delta y , \Delta f \)の平面の方程式です。

このことから、\( \Delta x \)や\( \Delta y \)が微小、つまり微小な範囲であれば、平面とみなせることになります。

なお3変数以上の関数であっても同様に、関数の変化分は変数が\( \Delta x, \Delta y , \Delta z \)などの一次式になり、線形（直線的な）関係が保持されます。

例題

1. \( \frac{\partial f}{\partial x} \) の計算：

\( x \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial x} = \frac{\partial}{\partial x} (2x^{3} + 3y^{2}z – 5xz^{2}) = 6x^{2} – 5z^{2} \)

2. \( \frac{\partial f}{\partial y} \) の計算：

\( y \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial y} = \frac{\partial}{\partial y} (2x^{3} + 3y^{2}z – 5xz^{2}) = 6yz \)

3. \( \frac{\partial f}{\partial z} \) の計算：

\( z \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial z} = \frac{\partial}{\partial z} (2x^{3} + 3y^{2}z – 5xz^{2}) = 3y^{2} – 10xz \)

1. \( \frac{\partial f}{\partial x} \) の計算：

\( x \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial x} = \frac{\partial}{\partial x} (e^{2x + 3y}) = 2e^{2x + 3y} \)

2.　\( \frac{\partial f}{\partial y} \) の計算：

\( y \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial y} = \frac{\partial}{\partial y} (e^{2x + 3y}) = 3e^{2x + 3y} \)

1. \( \frac{\partial f}{\partial x} \) の計算：

\( x \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial x} = \frac{\partial}{\partial x} (\log(2x) + \log(1-y)) = 2\frac{1}{2x} = \frac{1}{x} \)

2.　\( \frac{\partial f}{\partial y} \) の計算：

\( y \) 以外を定数とみなして微分します。

\( \hspace{10pt} \displaystyle \frac{\partial f}{\partial y} = \frac{\partial}{\partial y} (\log(2x) + \log(1-y)) = -\frac{1}{1-y} \)

何に使う？

機械学習の分野では極大値、極小値を見つけるために勾配ベクトルを利用することが多く、偏微分はその勾配ベクトルの計算に使われます。

「極大値、極小値」、「勾配ベクトル」については次のページをご覧ください。