勾配ベクトル

目次（このページで分かること）

勾配ベクトルとは何か？

勾配ベクトルとは、多変数関数から計算されるベクトルであり、その名の通り多変数関数の勾配（変化）の方向や大きさを表すベクトルです。

具体には次のような「方向」、「大きさ」をもちます。

方向　：多変数関数の変化率が最大になる方向
大きさ：上記方向の場合の傾き（変化率）

このページでは動かせる３Dグラフや図を使って、勾配ベクトルをグラフで見てみたり、定義式について視覚的に分かりやすく説明します。

その後、例題で勾配ベクトルを実際に計算してみます。

3Dグラフで勾配ベクトルを見てみましょう

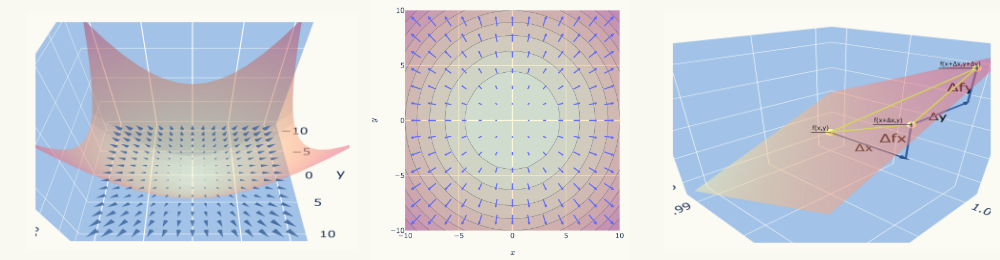
次のような2変数関数$ f(x,y) = x^{2} + y^{2} $の場合に勾配ベクトルがどうなるか、グラフで見てみましょう。

このグラフを見てわかるように、原点$ (x,y)=(0,0) $の点を最小値として、そこから離れるに従って関数値が大きくなっていくことが分かります。

また、原点$ (x,y)=(0,0) $付近と座標の端のグラフの傾斜を比べていただくと分かりますが、端の方が傾きが急、つまり変化率が大きくなっています。

このグラフはドラッグで回転などできますので、よかったら回転させて確認してみてください。

この関数の勾配ベクトルは下図のように、$ xy $平面上のベクトル（青い矢印）になります。

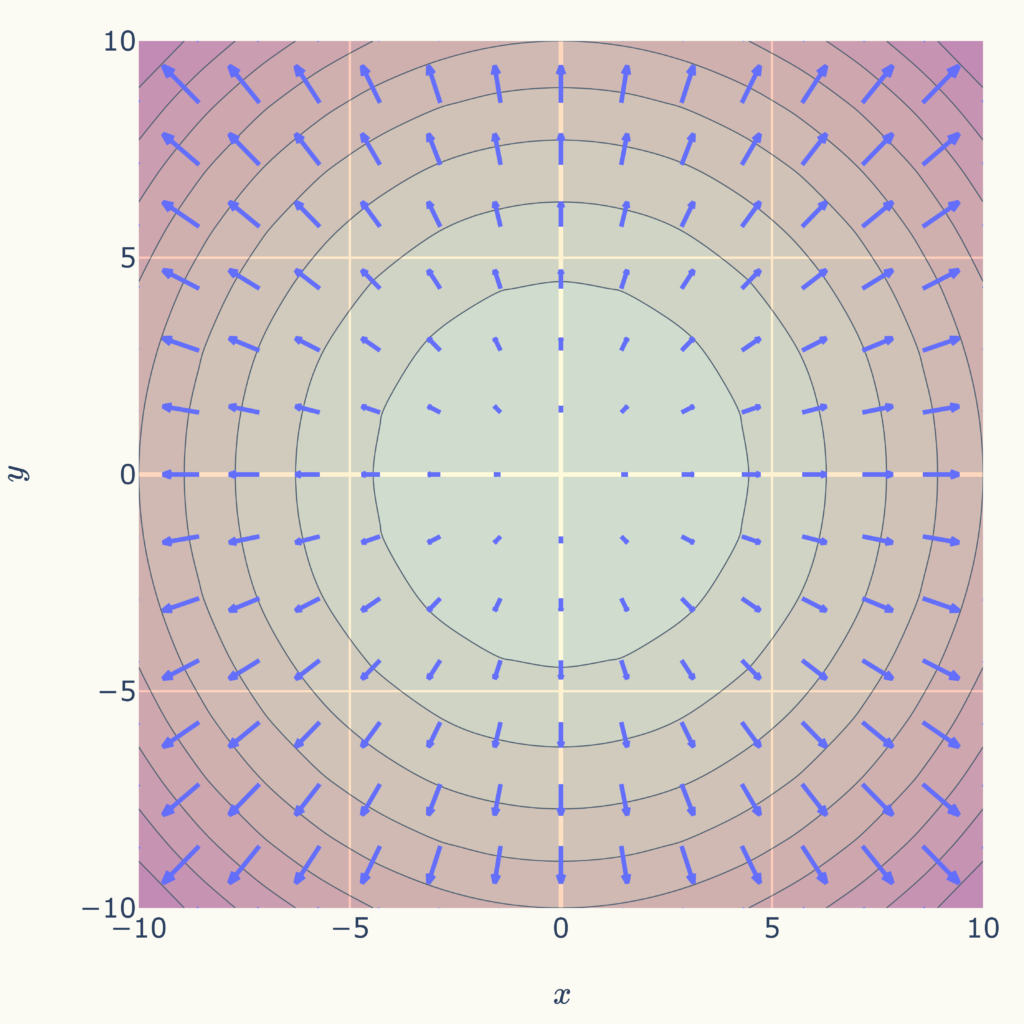
矢印は関数値が大きくなる方向を向いています。

また、原点$ (x,y)=(0,0) $から離れるに従って矢印自体が大きくなっていることが分かります。

これは関数値の変化率が原点$ (x,y)=(0,0) $から離れる方が大きくなることを示します。

ちなみに、円状の線は$ f(x,y) = x^{2} + y^{2} $の等高線です。

勾配ベクトルと関数グラフを同時にグラフ化

下図のように勾配ベクトルと関数グラフを同時にグラフ化すると分かりやすいかもしれません。

ただし、この図ではグラフ描画用プログラムの都合上、ベクトルをコーン状の形で表現しています。

コーンの方向がベクトルの方向、コーンの大きさがベクトルの大きさを表します。

このグラフもドラッグで回転などできますので、良かったら試してみてください。

勾配ベクトルの定義式

２変数関数$ f(x,y) $の場合

$$ \displaystyle 勾配ベクトル＝ \nabla f(x,y) = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} $$

3変数関数$ f(x,y,z) $の場合

$$ \displaystyle 勾配ベクトル＝ \nabla f(x,y,z) = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} + \frac{\partial f}{\partial z} \mathbf{k} $$

$ \nabla $は「ナブラ」と読み、上式のように$\nabla f(x,y) $とすると、$f(x,y) $の勾配ベクトルを計算する、という意味になります。

また、$ \partial $は偏微分記号、$ \mathbf{i} $、$ \mathbf{j} $、$ \mathbf{k} $は基底ベクトルです。

定義式の説明

ここでは、２変数関数の場合で説明します。

２変数関数$ f(x,y) $において、ある点$ (x,y) $から点$ (x+\Delta x,y+\Delta y) $に移動した場合の$ f $の変化量$ \Delta f = f(x+\Delta x,y+\Delta y)-f(x,y)$を求める事を考えます。

ただし、$ \Delta x $、$ \Delta y $は極々小さな値とします。

「偏微分」のページで見れますが、２変数関数のグラフは拡大することで平面となります。

つまり、ある点周辺の極々微小な範囲を考える場合、下図のように平面について考えればいいことになります。

このグラフはドラッグで回転などできます。

また同様に「偏微分」のページで解説していますが、偏微分の図形的な意味としては、グラフを平面になるまで拡大した時の、軸方向の傾き（変化率）を求めることです。

このことから、$ x $軸方向に$ \Delta x $移動するだけなら、$ f $の変化量は次式となります。

$ \hspace{10pt} \displaystyle fのx方向の変化量 = \Delta f_{x}= \frac{\partial f}{\partial x} \Delta x $

同様に$ y $軸方向は次式となります。

$ \hspace{10pt} \displaystyle fのy方向の変化量 = \Delta f_{y }= \frac{\partial f}{\partial y} \Delta y $

$ x $軸方向に$ \Delta x $、$ y $軸方向に$ \Delta y $移動した場合の変化量は下図のようになります。

このグラフはドラッグで回転などできます。

このグラフのように、トータルの$ f $の変化量$ \Delta f $は$ \Delta f_{x} $と$ \Delta f_{y} $の和になります。

$ \hspace{10pt} \displaystyle fの変化量 = \Delta f= \Delta f_{x } + \Delta f_{y } $

$ \hspace{20pt} \displaystyle = \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y $

上記の式は勾配ベクトル

$ \hspace{10pt} \displaystyle \nabla f(x,y) = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} $

と移動を表す次のベクトルを使用すると、

$ \hspace{10pt} \displaystyle \mathbf{r} = \Delta x \mathbf{i} + \Delta y \mathbf{j} $

これら二つのベクトルの内積になります。

$ \hspace{10pt} \displaystyle \Delta f = \nabla f(x,y) \cdot \mathbf{r}= \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y $

$ \hspace{20pt} \displaystyle = | \nabla f(x,y) | | \mathbf{r} | \cos \theta $

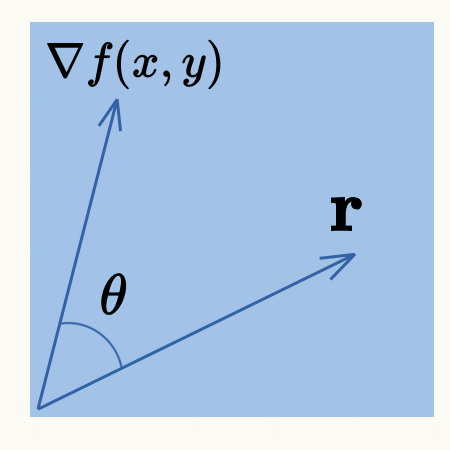
この式より、$ xy$平面上を任意方向に$ \mathbf{r} $だけ微小に移動した場合の関数$ f $の変化量$ \Delta f $を計算できます。

また、移動ベクトル$ \mathbf{r} $の方向が勾配ベクトル$ \nabla f(x,y) $と同じ場合、$ \cos \theta = \cos 0 = 1.0 $となり、変化量が最大になることが分かります。

つまり、勾配ベクトル$ \nabla f(x,y) $の「方向」は関数$ f(x,y) $が変化が最大となる方向になります。

また、この方向（$ \cos \theta = 1.0 $）の場合、勾配ベクトルの大きさ$ |\nabla f(x,y)| $に移動距離$ |\mathbf{r}| $をかけることで$ f(x,y) $の変化量になります。

$ \hspace{10pt} \displaystyle \Delta f = | \nabla f(x,y) | | \mathbf{r} | $

このことから、勾配ベクトルの「大きさ」は関数$ f(x,y) $が変化が最大となる方向に移動した場合の変化率となります。

例題

例題：$ f(x,y) = x^{2} +y^{2} $

関数 $ f(x,y) = x^{2} +y^{2} $ の勾配ベクトルを求めてください。

$ \hspace{10pt} \displaystyle 勾配ベクトル＝ \nabla f(x,y) = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} $

ですので、偏微分$ \frac{\partial f}{\partial x} $と$ \frac{\partial f}{\partial y} $を計算します。

$ \frac{\partial f}{\partial x} $ の計算では、$ x $ 以外を定数とみなして微分します。

$ \hspace{10pt} \displaystyle \frac{\partial f}{\partial x} = \frac{\partial}{\partial x} (x^{2} +y^{2} ) = 2x $

$ \frac{\partial f}{\partial y} $ の計算では、$ y $ 以外を定数とみなして微分します。

$ \hspace{10pt} \displaystyle \frac{\partial f}{\partial y} = \frac{\partial}{\partial y} (x^{2} +y^{2} ) = 2y $

よって、

$ 勾配ベクトル＝ \nabla f(x,y) = 2x \hspace{2pt} \mathbf{i} + 2y \hspace{2pt} \mathbf{j} $

となります。

何に使う？

極大値、極小値の探索

勾配ベクトルは多変数関数の極大値や極小値の探索に利用できます。

このことを感覚的にみるために、先程のグラフをもう一度示します。

先程書きましたが、この図では、勾配ベクトルをコーン状の形で表現しています。

コーンの方向がベクトルの方向、コーンの大きさがベクトルの大きさを表します。

このグラフもドラッグで回転などできます。

このグラフをみると関数が最小になる原点$ (x,y)=(0,0) $において、勾配ベクトルが見えないほど小さくなっていることが分かります。

「極大値、極小値」のページで、１変数関数の極小値（極大値）で微分がゼロになる解説をしましたが、同様に、多変数関数の極小値（極大値）では勾配ベクトルがゼロになります。

これを利用して勾配ベクトルで多変数関数の極大値や極小値の探索を行うことができます。

具体の応用としては次があります。

線形回帰

単線形回帰