単線形回帰とは何か?
単線形回帰は、実験値などの複数のデータの組が与えられた場合、そのデータ間の最ももっともらしい関係式を求める方法です。
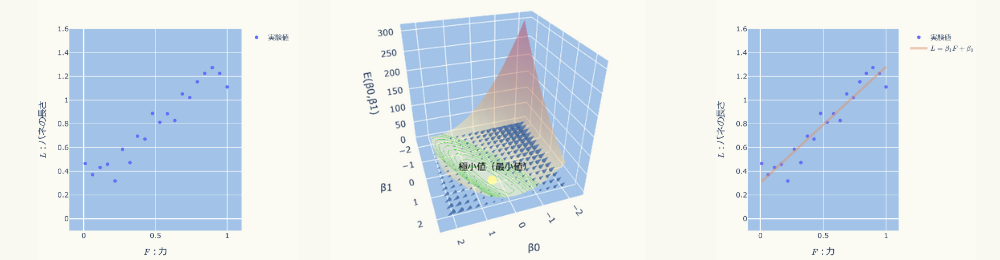
例えば、バネを引っ張る「力」と、その時のバネ「長さ」を計測した結果、以下のようなグラフになったとします。
データ間が一次関数(\( \displaystyle L = \beta_{1} F + \beta_{0}\))の関係にあると仮定し、単線形回帰により具体の関係式を求める( \( \beta_{0} \)、\( \beta_{1} \)を求める )と次式となります。
\( \displaystyle L = 0.97792 F + 0.30316 \)
グラフにすると以下となり、バラつきのある実験値の中央付近を通っていることが分かります。
関係式を得ることで任意の力\( F \)の値におけるバネの長さ\( L \)の推定値を得ることができるようになります。
このように単線形回帰ではデータの関係式の基本的な形(一次関数)を仮定し、その具体の係数を求める、という手順で、データの組の最ももっともらしい関係式を求めます。
具体の計算方法は下で解説します。
単線形回帰の計算
計算手順の概要
\( (x_{i},y_{i}) \hspace{10pt}i = 1 \cdots n \)
単線形回帰の場合は次式
\( y = \beta_{1} x + \beta_{0} \)
具体の計算方法
次のような\( n \)個のデータの組が与えられたとします。
| データNo. | \( x \) | \( y \) |
|---|---|---|
| 1 | \( x_{1} \) | \( y_{1} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( i \) | \( x_{i} \) | \( y_{i} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( n \) | \( x_{n} \) | \( y_{n} \) |
\( x_{i} \)や\( y_{i} \)は実際に計測された数値(例えばバネの「伸びの長さ」や「力の大きさ」など)です。
そして、データの関係式が次のような一次式になると仮定します。
$$ \displaystyle y = \beta_{1} x + \beta_{0}$$
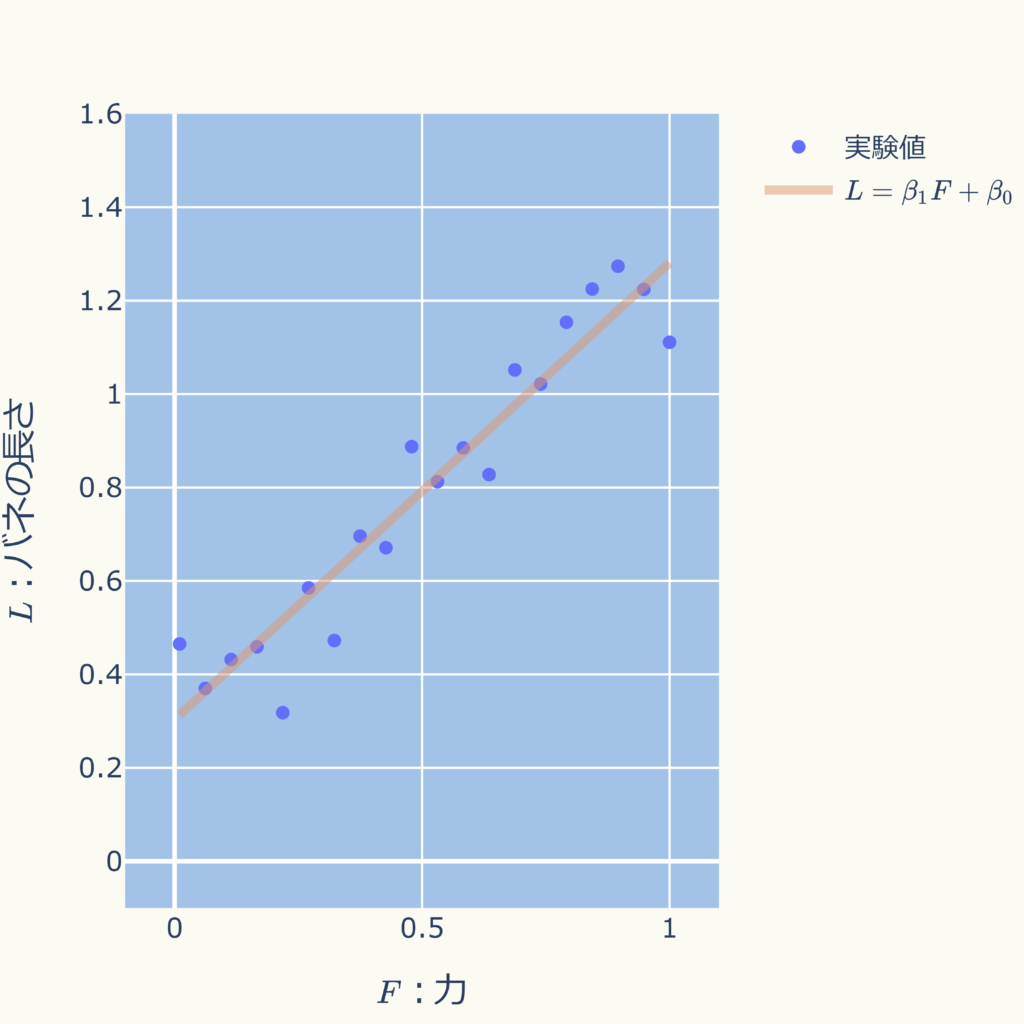
ここからは最小二乗法により、係数\( \beta_{1} \)、\( \beta_{0} \)を計算します。
この関係式により予測される\( \hat{y} = \beta_{1} x + \beta_{0} \)の値とデータとして与えられた\( y_{i} \)の値の差を誤差\( \epsilon_{i} \)とします。
\( \hspace{10pt} \displaystyle 誤差 \epsilon_{i} = y_{i} – \hat{y} \)
\( \hspace{35pt} \displaystyle = y_{i} -(\beta_{1} x + \beta_{0} x_{i}) \)
グラフにすると下図になります。
最小二乗法では、全てのデータの誤差の二乗を足し上げ(誤差の二乗和)、それを最小とするように\( \beta_{1} \)、\( \beta_{0} \)を決定します。
\( \hspace{10pt} \displaystyle 誤差の二乗和 \hspace{10pt} E(\beta_{0},\beta_{1}) = \sum_{i=1}^{n} \epsilon_{i}^{2} = \sum_{i=1}^{n} \left\{ y_{i} – (\beta_{1} x_{i} + \beta_{0}) \right\}^{2} \)
この誤差の二乗和の関数\( E(\beta_{0},\beta_{1}) \)は変数として\( \beta_{1} \)、\( \beta_{0} \)を持つ多変数関数です。
この\( E(\beta_{0},\beta_{1}) \)を展開すると、
\( \hspace{10pt} \displaystyle E(\beta_{0},\beta_{1}) = \sum_{i=1}^{n} \left\{ y_{i}^{2} – 2 y_{i} (\beta_{1} x_{i} + \beta_{0}) + (\beta_{1} x_{i} + \beta_{0})^{2} \right\} \)
\( \hspace{15pt} \displaystyle = \sum_{i=1}^{n} \left\{ y_{i}^{2} – 2 y_{i} (\beta_{1} x_{i} + \beta_{0}) + x_{i}^{2} \beta_{1}^{2} + 2 x_{i} \beta_{1} \beta_{0} + \beta_{0}^{2} \right\} \)
となり、変数である\( \beta_{1}^{2} \)、\( \beta_{0}^{2} \)の係数が正となるため、下のグラフのように下に凸の形状になります。
つまり、下に凸(谷底)のところで極小値(最小値)をとります。
また、多変数関数は極小値や極大値で勾配ベクトルがゼロとなります。
このグラフでは、コーン状の形で勾配ベクトルを表現しています。
コーンの方向がベクトルの方向、コーンの大きさがベクトルの大きさです。
谷底のところで勾配ベクトルのコーンが無くなっている(勾配ベクトルがゼロになる)ことが分かると思います。
このグラフはドラッグで回転できますので、よければ色々見てみてくださいね。
\( \hspace{10pt} \displaystyle 勾配ベクトル = \nabla E(\beta_{0},\beta_{1}) = \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{0}} \mathbf{i} + \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{1}} \mathbf{j} \)
ですので、基底ベクトル\( \mathbf{i} \)、\( \mathbf{j} \)の両方の係数がゼロのところで、極小値(最小値)となります。
\( \hspace{10pt} \displaystyle \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{0}} = 0 \hspace{10pt},\hspace{10pt} \displaystyle \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{1}} = 0 \)
これを計算すると、次式となります。
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i} + n \beta_{0} \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} x_{i} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i}^{2} + \beta_{0} \sum_{i=1}^{n} x_{i} \)
導出過程を見たい方はここをクリックして展開してください。
\( \hspace{10pt} \displaystyle \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{0}} = 0 \hspace{10pt},\hspace{10pt} \displaystyle \frac{\partial E(\beta_{0},\beta_{1})}{\partial \beta_{1}} = 0 \)
\( E(\beta_{0},\beta_{1}) \)を代入すると
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} \frac{ \partial \epsilon_{i}^{2} }{\partial \beta_{0}} = 0 \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} \frac{ \partial \epsilon_{i}^{2} }{\partial \beta_{1}} = 0 \)
ここで\( f(\epsilon) = \epsilon^{2} \)として、微分の連鎖律を使用すると、
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} \frac{ \partial f }{\partial \epsilon}\frac{ \partial \epsilon }{\partial \beta_{0}} = 0 \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} \frac{ \partial f }{\partial \epsilon}\frac{ \partial \epsilon }{\partial \beta_{1}} = 0 \)
ここで、
\( \hspace{10pt} \displaystyle \frac{ \partial f }{\partial \epsilon} = 2 \epsilon \)
\( \hspace{10pt} \displaystyle \frac{ \partial \epsilon }{\partial \beta_{0}} = -1 \)
\( \hspace{10pt} \displaystyle \frac{ \partial \epsilon }{\partial \beta_{1}} = -x_{i} \)
ですので、
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} -2 \epsilon = 0 \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} – 2 \epsilon x_{i} = 0 \)
誤差の定義式\( \displaystyle \epsilon_{i} = y_{i} -(\beta_{1} x_{i} + \beta_{0}) \)を代入すると
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} -2 \{ y_{i} -(\beta_{1} x_{i} + \beta_{0}) \} = 0 \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} – 2 \{ y_{i} -(\beta_{1} x_{i} + \beta_{0}) \} x_{i} = 0 \)
最終的に次式となります。
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i} + n \beta_{0} \hspace{10pt},\hspace{10pt} \displaystyle \sum_{i=1}^{n} x_{i} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i}^{2} + \beta_{0} \sum_{i=1}^{n} x_{i} \)
ここで、\( \displaystyle \sum_{i=1}^{n} \beta_{0} = n \beta_{0} \)を使いました。
この\( \beta_{1} \)、\( \beta_{0} \)に関する連立一次方程式を解くと最終的に次式となります。
\( \hspace{10pt} \displaystyle \beta_{0} = \bar{y} – \beta_{1} \bar{x} \)
\( \hspace{10pt} \)
\( \hspace{10pt} \displaystyle \beta_{1} = \frac{\displaystyle \frac{1}{n}\sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y})}{\displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\bar{x})^{2}} = \frac{s_{xy}}{s_{xx}} \)
これが誤差の二乗和が最小となる\( \beta_{1} \)、\( \beta_{0} \)です。
ここで、\( \bar{x} \)、\( \bar{y} \)は次式で計算される\( x_{i} \)、\( y_{i} \)の平均値です。
\( \hspace{10pt} \displaystyle \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} \)
\( \hspace{10pt} \displaystyle \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_{i} \)
また、\( s_{xy} \)、\( s_{xx} \)はそれぞれ\( x_{i} \)、\( y_{i} \)の共分散、\( x_{i} \)の分散と言われるもので、次式になります。
\( \hspace{10pt} \displaystyle s_{xy} = \frac{1}{n}\sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y}) \)
\( \hspace{10pt} \displaystyle s_{xx} = \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\bar{x})^{2} \)
導出過程を見たい方はここをクリックして展開してください。
\( \hspace{10pt} \displaystyle \sum_{i=1}^{n} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i} + n \beta_{0} \)
を\( \beta_{0} \)に関して解いて、
\( \hspace{10pt} \displaystyle \beta_{0} = \bar{y} – \beta_{1} \bar{x} \)
を得ます。
これを
\( \hspace{10pt} \displaystyle \displaystyle \sum_{i=1}^{n} x_{i} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i}^{2} + \beta_{0} \sum_{i=1}^{n} x_{i} \)
に代入すると、
\( \hspace{10pt} \displaystyle \displaystyle \sum_{i=1}^{n} x_{i} y_{i} = \beta_{1} \sum_{i=1}^{n} x_{i}^{2} + (\bar{y} – \beta_{1} \bar{x}) \sum_{i=1}^{n} x_{i} \)
\( \hspace{10pt} \displaystyle \left( \sum_{i=1}^{n} x_{i}^{2} – \bar{x}\sum_{i=1}^{n} x_{i} \right) \beta_{1} = \sum_{i=1}^{n} x_{i}y_{i} – \bar{y}\sum_{i=1}^{n} x_{i} \)
よって\( \beta_{1} \)は
\( \hspace{10pt} \displaystyle \beta_{1} = \frac{\displaystyle \sum_{i=1}^{n} x_{i}y_{i} – \bar{y}\sum_{i=1}^{n} x_{i}}{\displaystyle \sum_{i=1}^{n} x_{i}^{2} – \bar{x}\sum_{i=1}^{n} x_{i}} \)
右辺の分母、分子を\( n \)で割り\( x \)、\( y \)の平均\( \bar{x} \)、\( \bar{y} \)を使うと、
\( \hspace{15pt} \displaystyle = \frac{\displaystyle \frac{1}{n}\sum_{i=1}^{n} x_{i}y_{i} – \bar{x}\bar{y}}{\displaystyle \frac{1}{n} \sum_{i=1}^{n} x_{i}^{2} – \bar{x}^{2}} \)
この式の分母、分子それぞれを式変形していきます。
\( \hspace{10pt} \displaystyle 分母 = \frac{1}{n} \sum_{i=1}^{n} x_{i}^{2} – \bar{x}^{2} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n} \sum_{i=1}^{n} x_{i}^{2} – 2\bar{x}^{2} + \bar{x}^{2} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n} \sum_{i=1}^{n} x_{i}^{2} – 2\bar{x}\frac{1}{n}\sum_{i=1}^{n} x_{i} + \frac{1}{n} \sum_{i=1}^{n} \bar{x}^{2} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n} \sum_{i=1}^{n} (x_{i} – \bar{x})^{2} \)
\( \hspace{15pt} \displaystyle = s_{xx} \)
次に分子は
\( \hspace{10pt} \displaystyle 分子 = \frac{1}{n}\sum_{i=1}^{n} x_{i}y_{i} – \bar{x}\bar{y} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n}\sum_{i=1}^{n} x_{i}y_{i} – \bar{x}\bar{y} – \bar{x}\bar{y} + \bar{x}\bar{y} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n}\sum_{i=1}^{n} x_{i}y_{i} – \sum_{i=1}^{n} x_{i} \bar{y} – \sum_{i=1}^{n}\bar{x}y_{i} + \frac{1}{n}\sum_{i=1}^{n}\bar{x}\bar{y} \)
\( \hspace{15pt} \displaystyle = \frac{1}{n}\sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y}) \)
\( \hspace{15pt} \displaystyle = s_{xy} \)
以上から、
\( \hspace{10pt} \displaystyle \beta_{1} = \frac{\displaystyle \frac{1}{n}\sum_{i=1}^{n} (x_{i}-\bar{x})(y_{i}-\bar{y})}{\displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\bar{x})^{2}} = \frac{s_{xy}}{s_{xx}} \)
を得ます。
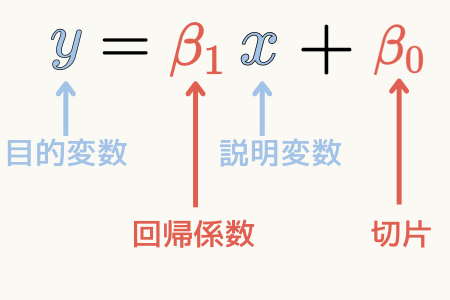
用語説明
単線形回帰では各記号を以下のように呼んだりします。
例題:バネの実験
あるバネについて、「伸び」とその時のバネの引っ張る「力」を計測する実験を20回行ったところ、以下の計測値が得られたとします。
| データNo. | \( F \):力 | \( L \):バネの長さ |
|---|---|---|
| 1 | 0.01 | 0.46513 |
| 2 | 0.06211 | 0.37002 |
| 3 | 0.11421 | 0.43161 |
| 4 | 0.16632 | 0.45908 |
| 5 | 0.21842 | 0.31799 |
| 6 | 0.27053 | 0.58499 |
| 7 | 0.32263 | 0.47251 |
| 8 | 0.37474 | 0.69585 |
| 9 | 0.42684 | 0.67102 |
| 10 | 0.47895 | 0.8874 |
| 11 | 0.53105 | 0.81242 |
| 12 | 0.58316 | 0.88462 |
| 13 | 0.63526 | 0.82771 |
| 14 | 0.68737 | 1.05159 |
| 15 | 0.73947 | 1.02144 |
| 16 | 0.79158 | 1.15361 |
| 17 | 0.84368 | 1.22478 |
| 18 | 0.89579 | 1.27358 |
| 19 | 0.94789 | 1.22415 |
| 20 | 1 | 1.11081 |
グラフにすると下図になります。

関係式が次式のような一時式に従うと仮定し、単線形回帰を適用してみます。
\( \displaystyle L = \beta_{1} F + \beta_{0} \)
先程の\( \beta_{0} \)、\( \beta_{1} \)を求める式におい\( n \)⇒\( 20 \)、\( x \)⇒\( F \)、\( y \)⇒\( L \)と置き換えると、次式になります。
\( \hspace{10pt} \displaystyle \beta_{0} = \bar{L} – \beta_{1} \bar{F} \)
\( \hspace{10pt} \displaystyle \beta_{1} = \frac{\displaystyle \frac{1}{20}\sum_{i=1}^{20} (F_{i}-\bar{F})(L_{i}-\bar{L})}{\displaystyle \frac{1}{20} \sum_{i=1}^{20} (F_{i}-\bar{F})^{2}} = \frac{s_{FL}}{s_{FF}} \)
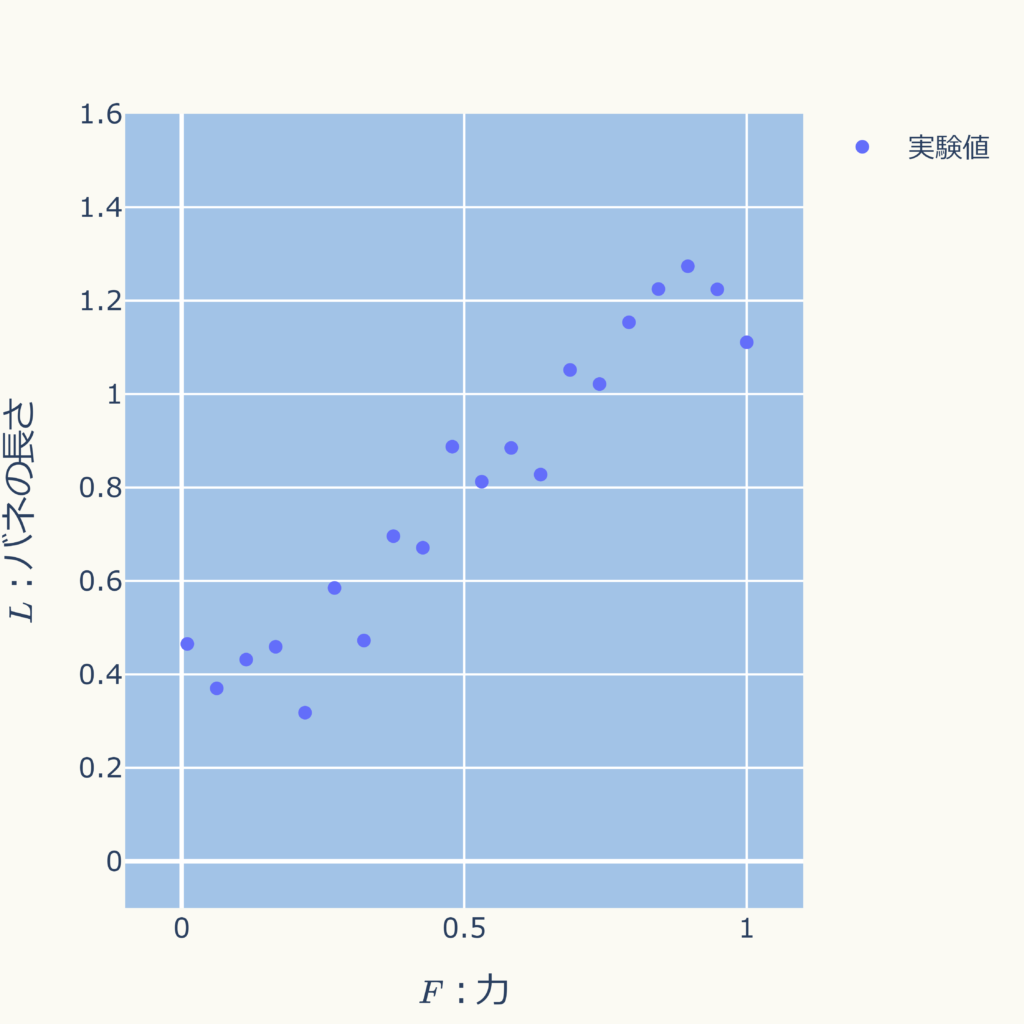
これを具体に計算すると、推定される関係式は
\( \displaystyle L = 0.97792 F + 0.30316 \)
となります。
グラフにすると下図となり、バラツキの中心付近を通ります。

ちなみに、誤差の二乗和 \( \hspace{10pt} E(\beta_{0},\beta_{1}) \)をグラフにすると次図になります。
このグラフは回転できます。
Webページの表示速度が遅くなるため、少ないデータでグラフ化しているので等高線がカクカクしてすみません。
ですが、計算した極小値の位置(黄色い丸 \( \beta_{1} = 0.97792 \)、\( \beta_{0} = 0.30316 \) )が谷底の位置(最小値)になっていることが分かるかと思います。
Pythonによる計算
機械学習ライブラリを使用しない場合
コード全体と出力結果
import numpy as np
# データ生成用関数
def f(x):
np.random.seed(14)
return x + 0.3 + np.random.normal(0, 0.1, size=len(x))
# データ数
n = 20
# データ生成
x = np.linspace(0.01, 1, n)
y = f(x)
# 係数計算
beta1 = ( 1/n*np.dot(x- np.mean(x), y- np.mean(y)) )/ ( 1/n*np.dot(x - np.mean(x), x - np.mean(x)) )
beta0 = np.mean(y) - beta1*np.mean(x)
# 結果表示
print('回帰変数 beta1: %.5f' %beta1)
print('切片 beta0: %.5f' %beta0)
print('y= %.5fx + %.5f' % (beta1 , beta0))
# 出力
回帰変数 beta1: 0.97792
切片 beta0: 0.30316
y= 0.97792x + 0.30316コード解説
- 「データ生成用関数」部分で、「\( x \) + 0.3 + 乱数 」の関数を定義し、これを基にデータの組を作成
- データ数 \( n= 20 \)
- 上で導出した式を使って\( \beta_{1} \)回帰係数と、\( \beta_{0} \)切片を計算
- 計算の際はnumpyライブラリで平均(np.mean)やデータの掛け算(np.dot)を行う
- 最後に係数を画面出力
機械学習ライブラリを使用した場合
コード全体と出力結果
import numpy as np
from sklearn.linear_model import LinearRegression
# データ生成用関数
def f(x):
np.random.seed(14)
return x + 0.3 + np.random.normal(0, 0.1, size=len(x))
# データ数
n = 20
# データ生成
x = np.linspace(0.01, 1, n)
y = f(x)
# 単線形回帰
model = LinearRegression()
model.fit(x.reshape(-1, 1), y)
# 結果表示
print('回帰変数 beta1: %.5f' %model.coef_[0])
print('切片 beta0: %.5f' %model.intercept_)
print('y= %.5fx + %.5f' % (model.coef_[0] , model.intercept_))
# 出力
回帰変数 beta1: 0.97792
切片 beta0: 0.30316
y= 0.97792x + 0.30316コード解説
- 「データ生成用関数」部分で、「\( x \) + 0.3 + 乱数 」の関数を定義し、これを基にデータの組を作成
- データ数 \( n= 20 \)
- 機械学習ライブラリ scikit-learn(sklearn)を使ってβ1回帰係数と、β0切片を計算
- 最後に係数を画面出力