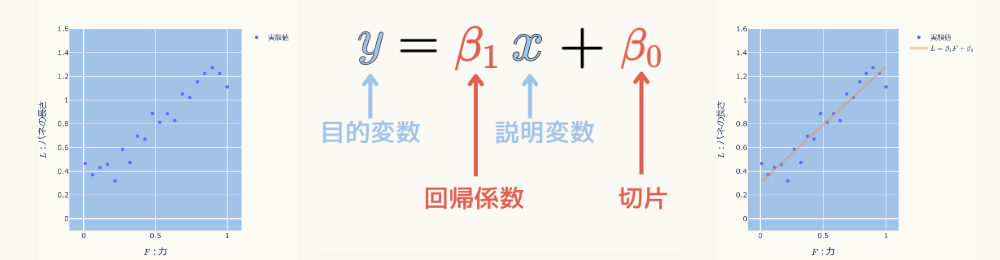
最小二乗法とは何か?
最小二乗法は、実験値などの複数の計測データの組が与えられた場合、そのデータ間の最ももっともらしい関係式を求める方法です。
例えば、あるバネの「伸び」とその時のバネを引っ張る「力」を計測した結果、以下のようなグラフになったとします。
データ間が一次関数(\( \displaystyle l = \beta F \))の関係にあると仮定し、最小二乗法により具体の関係式を求める( \( \displaystyle \beta \)を求める )と次式となります。
\( \displaystyle l = 0.9825 F \)
グラフにすると以下となり、バラつきのある実験値の中央付近を通っていることが分かります。
関係式を得ることで任意の力\( F \)の値におけるバネの伸び\( l \)の推定値を得ることができるようになります。
このように最小二乗法ではデータの関係式の基本的な形(一次関数など)を仮定し、その具体の係数を求める、という手順で、データの組の最ももっともらしい関係式を求めます。
具体の計算方法は下で解説します。
最小二乗法の計算方法(係数が一つの場合)
このページでは求める係数が一つ( \( \beta\)だけ )の最も単純なケースで最小二乗法を解説します。
係数が2つの場合は単線形回帰で解説しています。(単線形回帰は係数が2つの最小二乗法です)
計算手順の概要
\( (x_{i},y_{i}) \hspace{10pt}i = 1 \cdots n \)
\( y = \beta x \)
具体の計算方法
次のような\( n \)個のデータの組が与えられたとします。
| データNo. | \( x \) | \( y \) |
|---|---|---|
| 1 | \( x_{1} \) | \( y_{1} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( i \) | \( x_{i} \) | \( y_{i} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( n \) | \( x_{n} \) | \( y_{n} \) |
\( x_{i} \)や\( y_{i} \)は実際に計測された数値(例えばバネの「伸びの長さ」や「力の大きさ」など)です。
そして、データの関係式が次のような一次式になると仮定します。
$$ \displaystyle y = \beta x $$
この関係式による予測される\( \hat{y} = \beta x_{i} \)の値とデータとして与えられた\( y_{i} \)の値の差を誤差\( \epsilon_{i} \)とします。
\( \hspace{10pt} \displaystyle 誤差 \epsilon_{i} = y_{i} – \hat{y} \)
\( \hspace{35pt} \displaystyle = y_{i} -(\beta x_{i}) \)
グラフにすると下図になります。
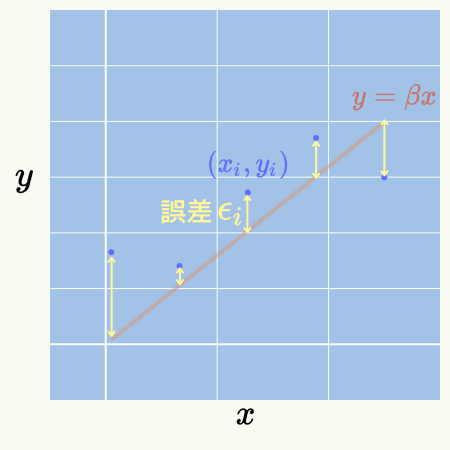
最小二乗法では、全てのデータの誤差の二乗を足し上げ(誤差の二乗和)、それを最小とするように\( \beta \)を決定します。
\( \hspace{10pt} \displaystyle 誤差の二乗和 = \sum_{i=1}^{n} \epsilon_{i}^{2} = \sum_{i=1}^{n} \left\{ y_{i} -(\beta x_{i}) \right\}^{2} \)
この式を\( \beta \)に関する式にするため、展開して整理すると、
(スマホでご覧の方へ、画面から見切れてしまう式は横スクロールできます)
\( \hspace{20pt} \displaystyle = \sum_{i=1}^{n} \left\{ y_{i}^{2} -2y_{i}(\beta x_{i}) +(\beta x_{i})^{2} \right\} \)
\( \hspace{20pt} \displaystyle = \sum_{i=1}^{n}y_{i}^{2} -2\sum_{i=1}^{n}y_{i}(\beta x_{i}) +\sum_{i=1}^{n}(\beta x_{i})^{2} \)
\( \hspace{20pt} \displaystyle = \left( \sum_{i=1}^{n}y_{i}^{2} \right) – 2\left( \sum_{i=1}^{n}x_{i} y_{i} \right) \beta +\left( \sum_{i=1}^{n}x_{i}^{2} \right) \beta^{2} \)
\( \hspace{20pt} \displaystyle = \left( \sum_{i=1}^{n}x_{i}^{2} \right) \beta^{2} – 2\left( \sum_{i=1}^{n}x_{i} y_{i} \right) \beta + \left( \sum_{i=1}^{n}y_{i}^{2} \right) \)
となり、\( \beta \)に関する二次関数になります。
括弧付きの\( \sum \)のところは実験結果から算出される定数です。
\( \beta^{2} \)の係数\( \displaystyle \left( \sum_{i=1}^{n}x_{i}^{2} \right) \)は必ずプラスとなるため、この関数は\( f(x) = x^{2} \)のように、下に凸の外形になります。
このため、微分値ゼロのところで極小値(最小値)になります。
\( \beta \)についての微分がゼロとは
\( \hspace{10pt} \displaystyle \frac{ d \left( 誤差の二乗和 \right) }{d \beta} \hspace{15pt} = 2 \left( \sum_{i=1}^{n}x_{i}^{2} \right) \beta – 2\left( \sum_{i=1}^{n}x_{i} y_{i} \right) = 0\)
となります。
よって、
$$ \hspace{10pt} \displaystyle \beta = \frac{\displaystyle \sum_{i=1}^{n}x_{i} y_{i} }{\displaystyle \sum_{i=1}^{n}x_{i}^{2} } $$
で「誤差の二乗和」は極小値(最小値)となります。
この\( \beta \)を最初に仮定した関係式\( \displaystyle y = \beta x \)に代入すると、データの組の最終的な関係式は次式となります。
$$ \hspace{10pt} \displaystyle y = \left( \frac{\displaystyle \sum_{i=1}^{n}x_{i} y_{i} }{\displaystyle \sum_{i=1}^{n}x_{i}^{2} } \right) x $$
例題:バネの実験
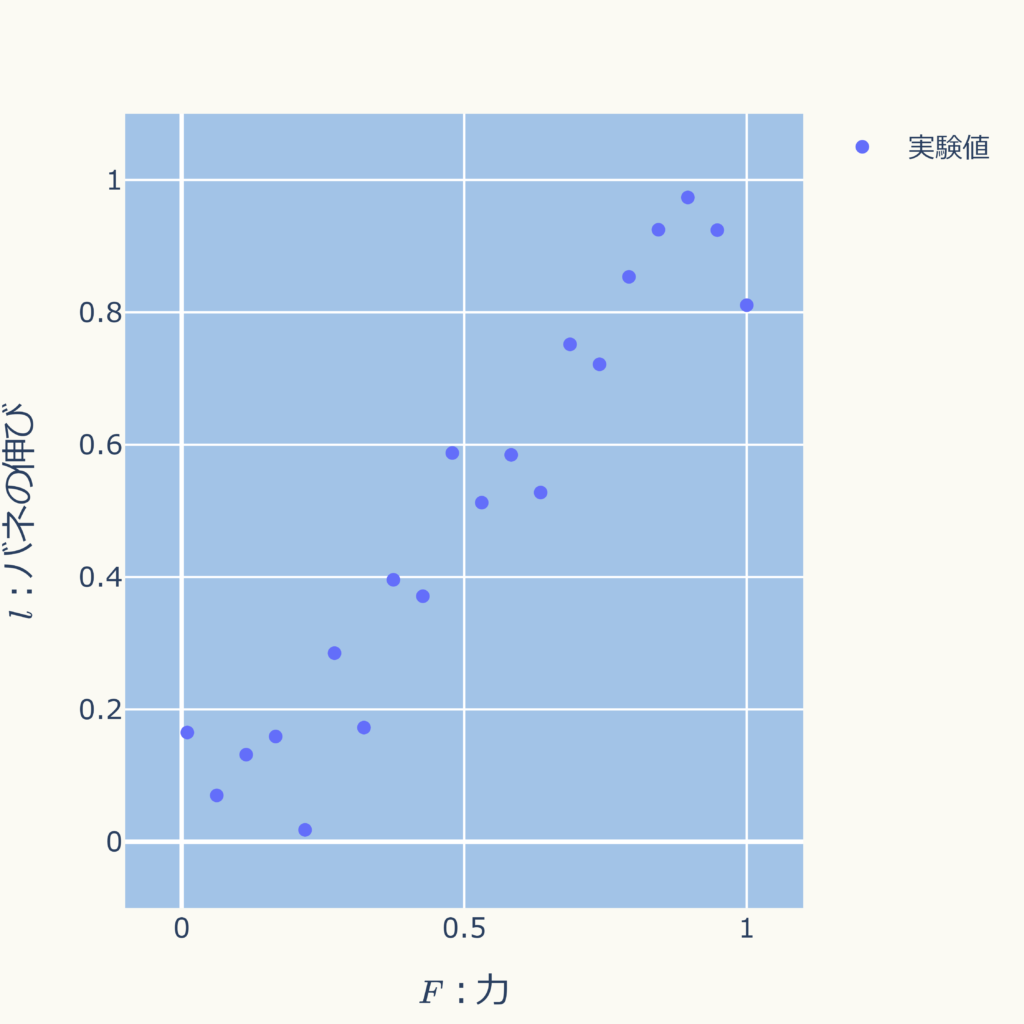
あるバネについて、「伸び」とその時のバネの引っ張る「力」を計測する実験を20回行ったところ、以下の計測値が得られたとします。
| データNo. | \( F \):力 | \( l \):バネの伸び |
|---|---|---|
| 1 | 0.01 | 0.16513 |
| 2 | 0.06211 | 0.07002 |
| 3 | 0.11421 | 0.13161 |
| 4 | 0.16632 | 0.15908 |
| 5 | 0.21842 | 0.01799 |
| 6 | 0.27053 | 0.28499 |
| 7 | 0.32263 | 0.17251 |
| 8 | 0.37474 | 0.39585 |
| 9 | 0.42684 | 0.37102 |
| 10 | 0.47895 | 0.5874 |
| 11 | 0.53105 | 0.51242 |
| 12 | 0.58316 | 0.58462 |
| 13 | 0.63526 | 0.52771 |
| 14 | 0.68737 | 0.75159 |
| 15 | 0.73947 | 0.72144 |
| 16 | 0.79158 | 0.85361 |
| 17 | 0.84368 | 0.92478 |
| 18 | 0.89579 | 0.97358 |
| 19 | 0.94789 | 0.92415 |
| 20 | 1 | 0.81081 |
グラフにすると下図になります。

関係式が次式のような一次式に従うと仮定し、最小二乗法を適用してみます。
\( \displaystyle l = \beta F \)
先程の\( \beta \)を求める式におい\( n \)⇒\( 20 \)、\( x \)⇒\( F \)、\( y \)⇒\( l \)と置き換えると、次式になります。
\( \hspace{10pt} \displaystyle \beta = \frac{\displaystyle \sum_{i=1}^{20}F_{i} l_{i} }{\displaystyle \sum_{i=1}^{20}F_{i}^{2} } \)
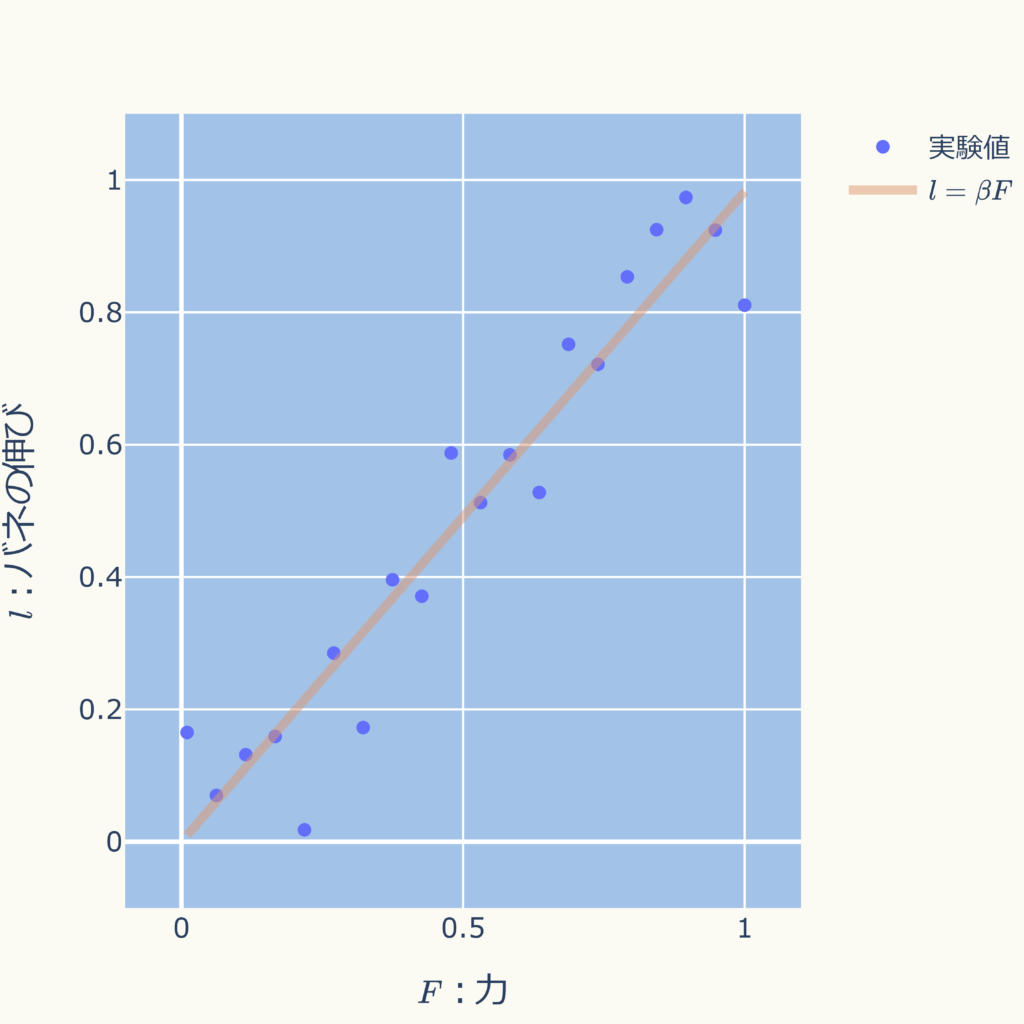
これを具体に計算すると\( \beta=0.9825 \)となり、推定される関係式は
\( \displaystyle l = 0.9825 F \)
となります。
グラフにすると下図となり、バラツキの中心付近を通ります。

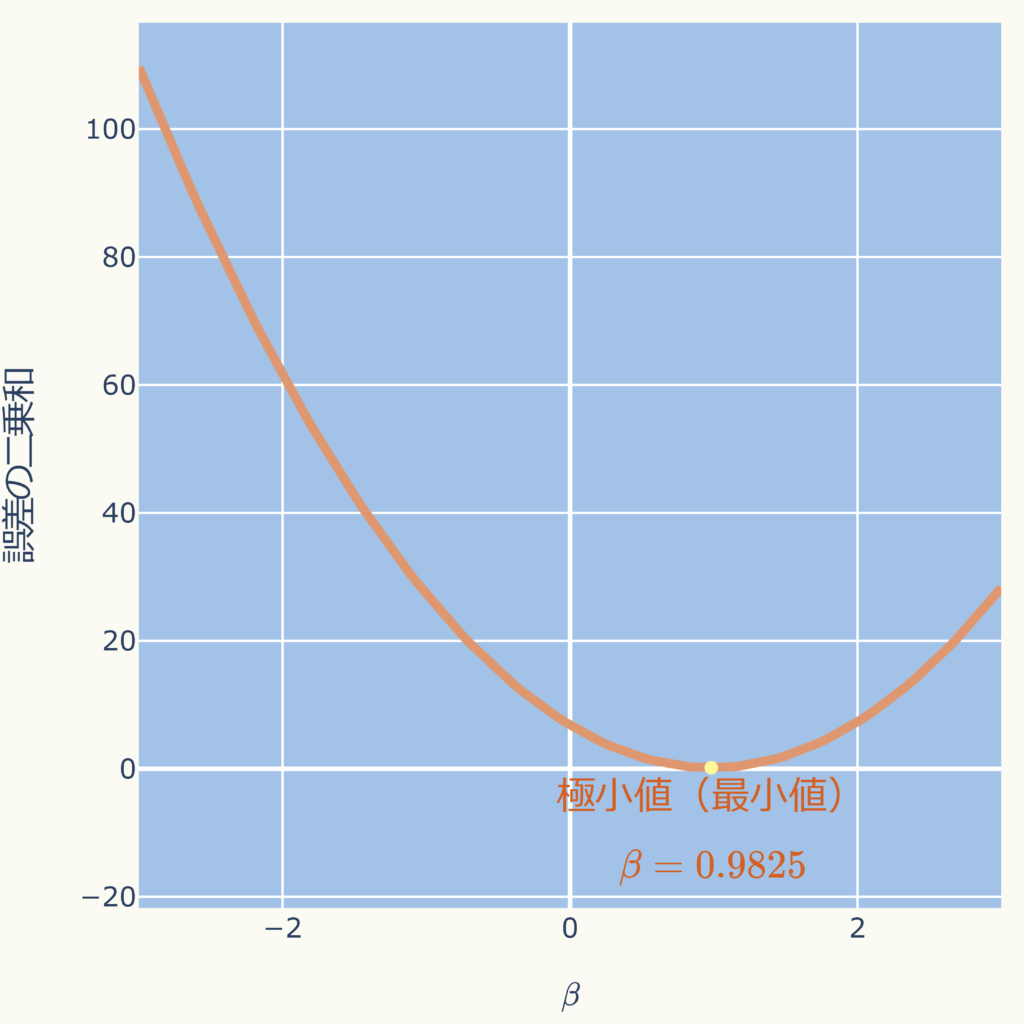
ちなみに、誤差の二乗和をグラフにすると次図になり、\( \beta=0.9825 \)で極小値(最小値)になります。
何に使う?
回帰分析
回帰分析も目的は「データ間の関係式を求める」ことです。
そして、回帰分析からすると最小二乗法はその手段の一つです。
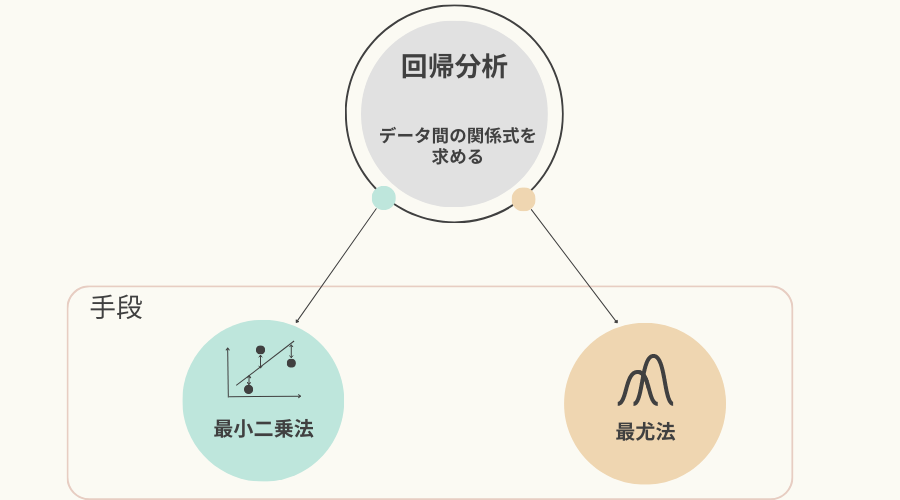
この記事では、最も単純なケース(求める関係式の係数が一つの場合)で最小二乗法を解説しましたが、回帰分析の手法である単線形回帰や重線形回帰は関係式の係数が複数の場合の最小二乗法です。
このため、最小二乗法の基本的な考え方がわかり、なおかつ、多変数関数の最小値の求め方(勾配ベクトルがゼロ)が分かれば、単線形回帰、重線形回帰も理解できます。
なお、最尤法を用いても、最小二乗法と同じ関係式を導出できますが、最小二乗法による導出で十分と思われますので、割愛します。
単線形回帰については、次のページをご覧ください。