極大値、極小値、極値とは?
下図のように、極大値とはグラフの山頂の値であり、極小値は谷底の値です。
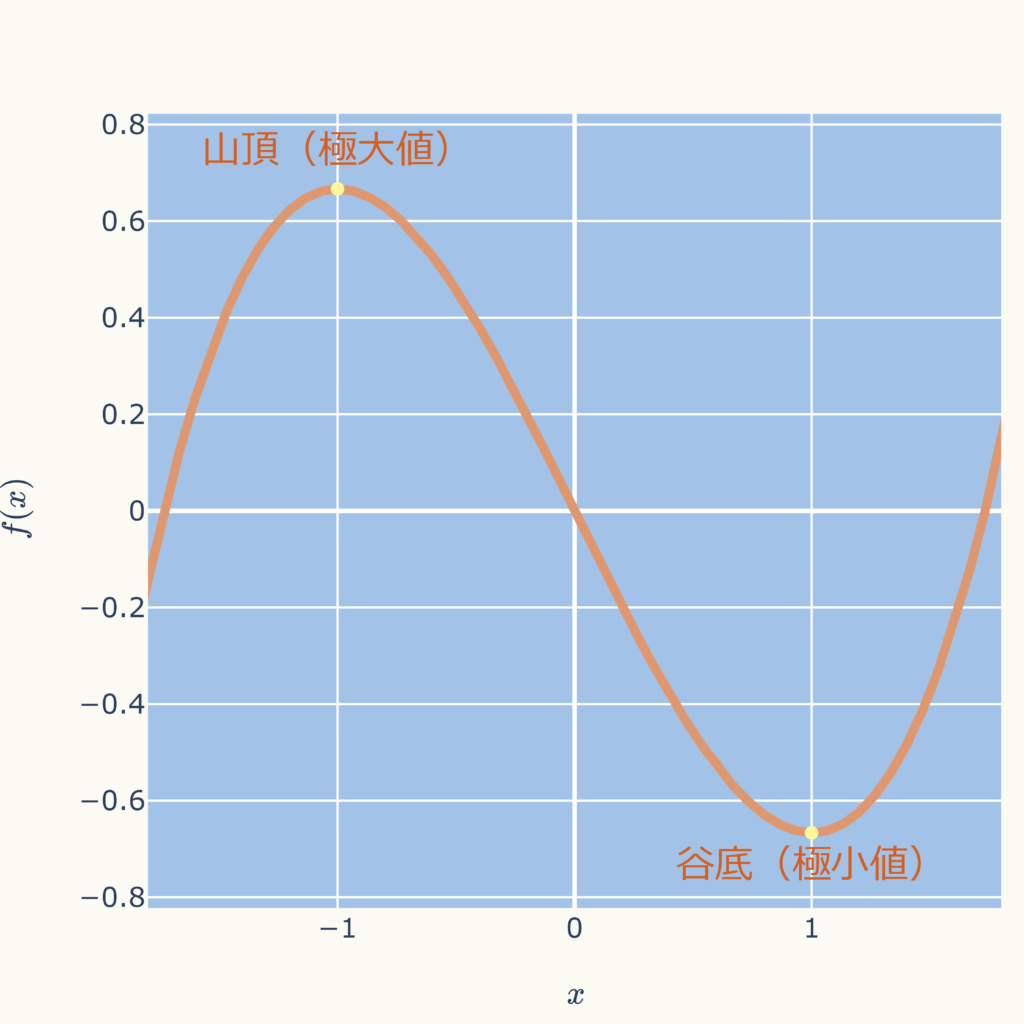
なお、極大値、極小値をまとめて極値と言います。
極値は微分を使って求める事ができ、機械学習の分野では下の動画のようにコンピュータを使用した反復計算で極値を求める手法がよく使わます。
(勾配降下法と言います。)
このページでは動画や図を使って、極値と最大値、最小値との違い、微分を使った極値の求め方(「極値判別法と増減表」と「勾配降下法」)を解説し、例題を解いてみます。
最大値、最小値との違い
最大値とはその名の通り、検討している\( x \) の区間の関数\( f(x) \) の最大の値であり、最小値は最小の値です。
上のグラフにおいては極大値=最大値、極小値=極小値になっていました。
しかし、下のようなグラフの場合は、最大値、最小値はグラフの端部にあります。
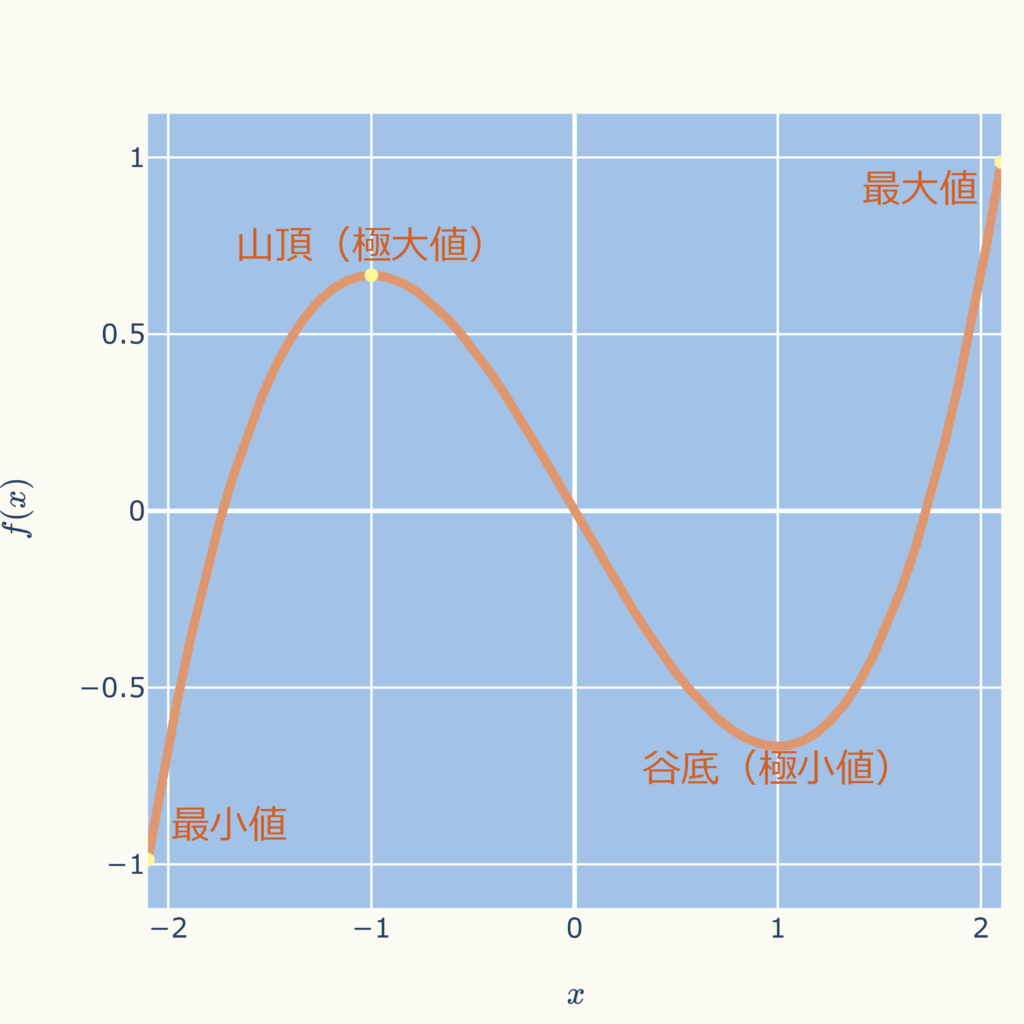
このように極値は必ずしも最大値や最小値になりませんので、注意が必要です。
極大値、極小値の求め方
ここでは極大値、極小値の求め方として、「極値判別法と増減表」と「勾配降下法(最急降下法)」を説明します。
- 主に手計算で求める方法
- 極小値、極大値の両方を求める事ができます
- 極小値、極大値と微分の関係を理解できます
- コンピュータを使って計算する手法
- 求まるのは極小値のみ
- 機械学習やAIといった分野において、広く利用されています
極値判別法と増減表
例として、次のグラフのように\( \displaystyle \hspace{5pt} f(x) = \frac{x(x^{2}-3)}{3} \hspace{5pt} \)の\( \hspace{5pt} -1.8 \text{≦} x \text{≦} +1.8 \hspace{5pt} \)の範囲を考えます。
微分を利用して極値を見つけます。
次の動画のように微分とはグラフを直線になるまで拡大した際の変化率(傾き)を求めることです。
(微分について詳しく知りたい方は、「微分の基礎」をご覧ください。)
グラフを拡大すると直線になる、ということは、それは逆に見れば次の動画のように、曲線のグラフも微小な直線の連続とみなせる、ということです。
そこで、実際にこのグラフを直線の連続として表現してみます。
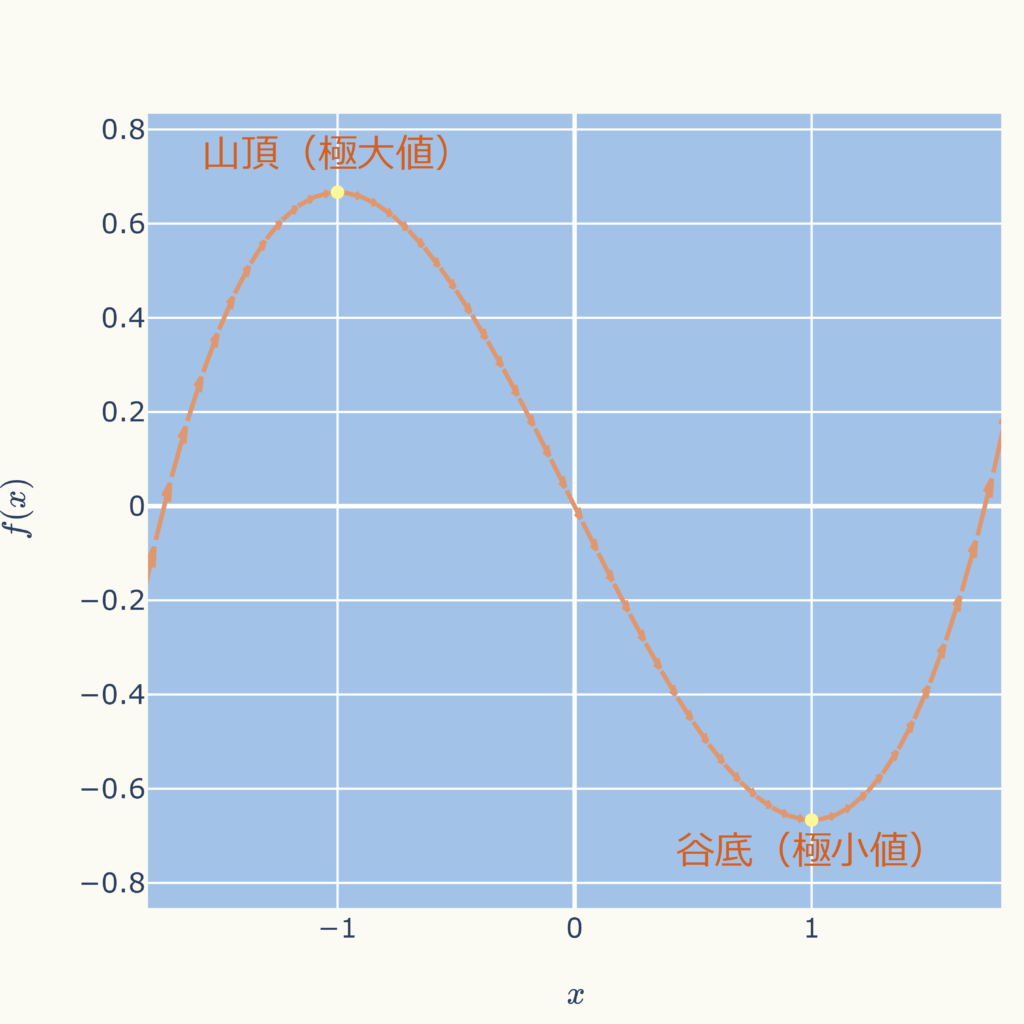
これは\( -1.8 \text{≦} x \text{≦} +1.8 \)の区間を60程度に分割して直線の連続としてグラフ化したものです。
山頂付近を拡大すると次のグラフになります。
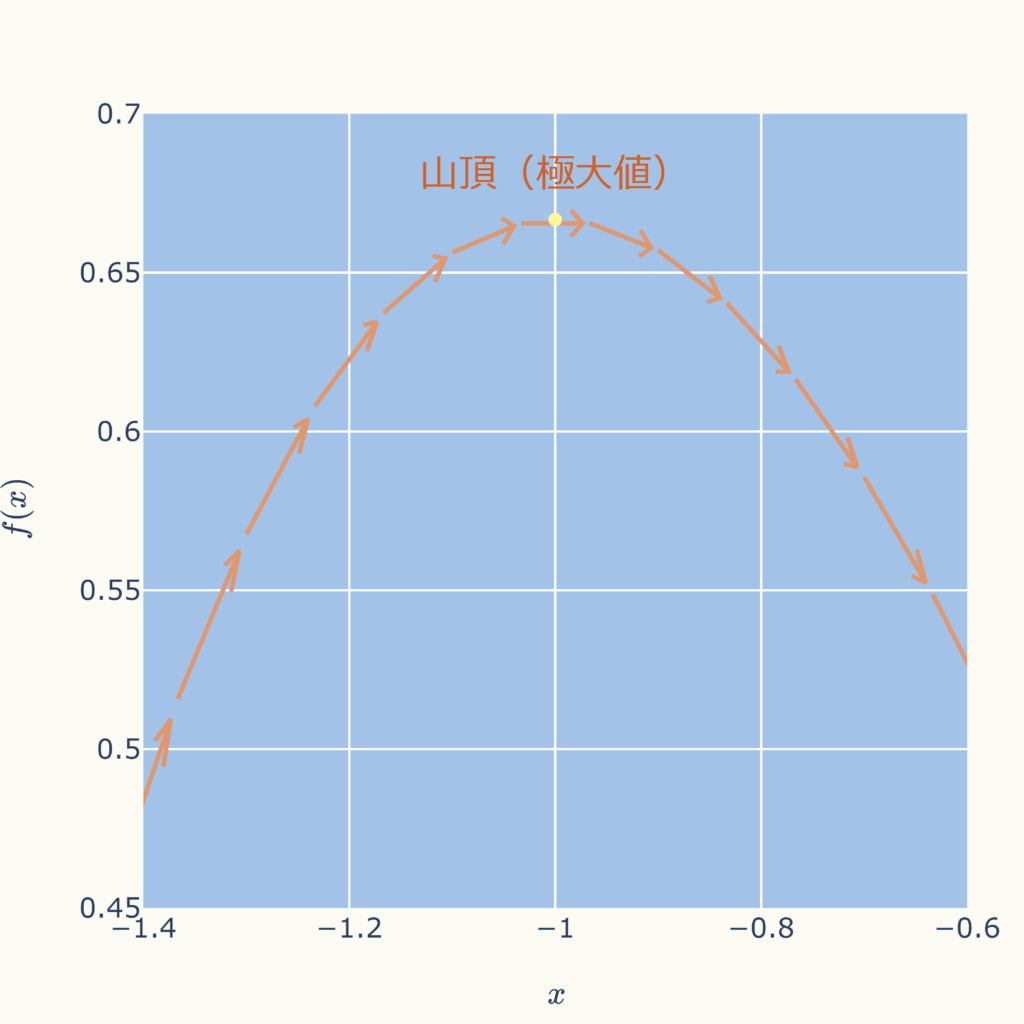
山頂では直線の傾きがゼロ(x軸と並行)、つまり微分値がゼロになっています。
さらに、その前後で直線の傾き(微分値)はプラス(上向き)からマイナス(下向き)に変化していることが分かります。
次に谷底付近を拡大してみます。
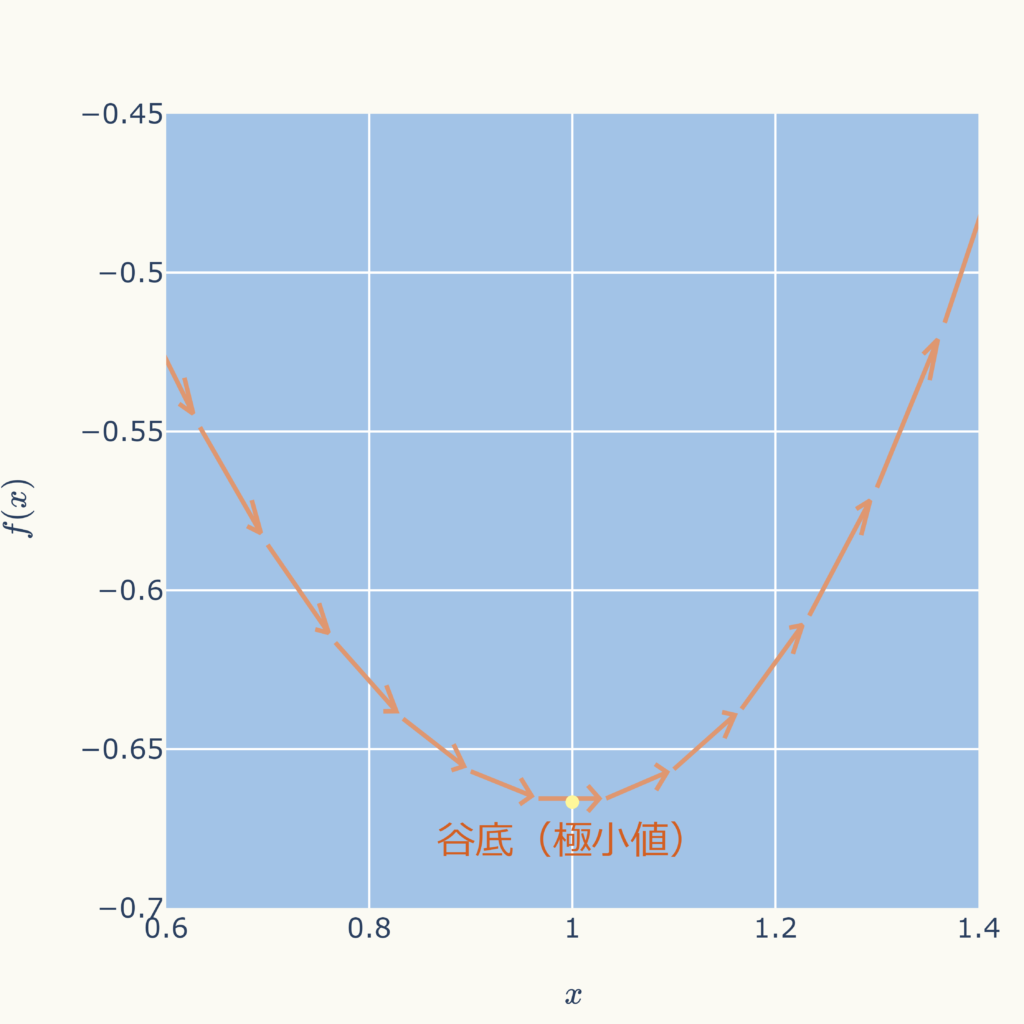
谷底でも直線の傾きがゼロ(x軸と並行)、微分値がゼロになっています。
その前後で直線の傾き(微分値)は逆にマイナス(下向き)からプラス(上向き)に変化していることが分かります。
まとめると、次の判別法となります。
関数\( f(x) \)の微分値が\( x=a \)でゼロになるとする。
- \( x=a \)で微分値がプラスからマイナスに変わるなら、\( f(x) \)は\( x=a \)で極大値をとる。
- \( x=a \)で微分値がマイナスからプラスに変わるなら、\( f(x) \)は\( x=a \)で極小値をとる。
具体に微分の公式を使用して計算してみます。
スマホでご覧の方へ。画面からはみ出すような式は横スクロールできます。
\( \hspace{10pt} \displaystyle f(x) = \frac{x(x^{2}-3)}{3} \)
\( \hspace{30pt} \displaystyle = \frac{1}{3}x^{3} – x \)
ここで、べき関数の微分の公式
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)
を使うと、
\( \hspace{10pt} \displaystyle f^{\prime}(x) = x^{2} – 1 \)
\( \hspace{30pt} \displaystyle = (x-1)(x+1) \)
以上から微分値がゼロになるのは\( \hspace{5pt} x = -1,+1 \hspace{5pt} \)のところであり、そこで山頂か谷底になることが分かります。
上のグラフを見ると、どちらが山頂か谷底なのか一目瞭然ですが、ここではあえてグラフの形状が不明であると仮定して山頂と谷底を判別してみます。
次のことを調べて表にします。
- \( \hspace{5pt} x = -1,+1 \hspace{5pt} \)の前後の\( f^{\prime}(x) \)の符号(プラス、マイナス)
- \( \hspace{5pt} x = -1,+1 \hspace{5pt} \)における\( f(x) \)の値
- 検討範囲\( \hspace{5pt} -1.8 \text{≦} x \text{≦} +1.8 \hspace{5pt} \)の両端、\( \hspace{5pt} x = -1.8,+1.8 \hspace{5pt} \)における\( f(x) \)の値
すると次表になり、このような表を増減表と呼びます。
| \( x \) | -1.8 | -1 | +1 | +1.8 | |||
| \( f^{\prime}(x) \) | + | + | 0 | – | 0 | + | + |
| \( f(x) \) | -0.144 | ↗ | 0.667 | ↘ | -0.667 | ↗ | +0.144 |
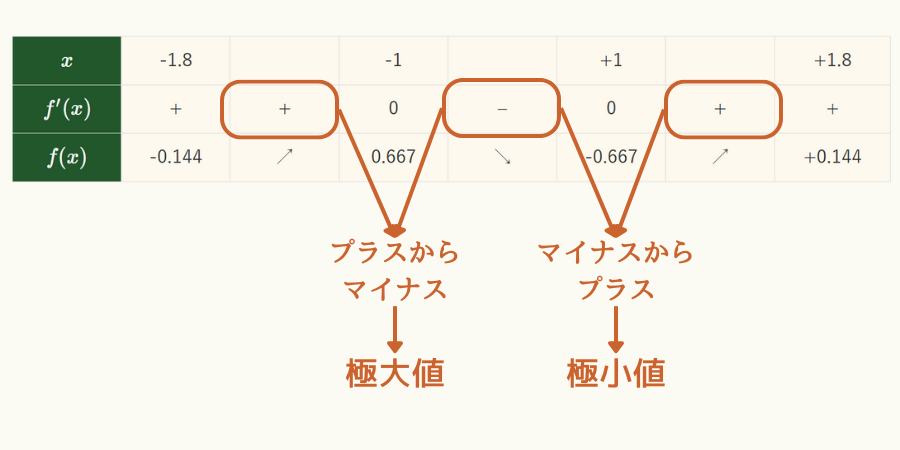
この増減表から次のことが分かります。
- 極大値、極小値
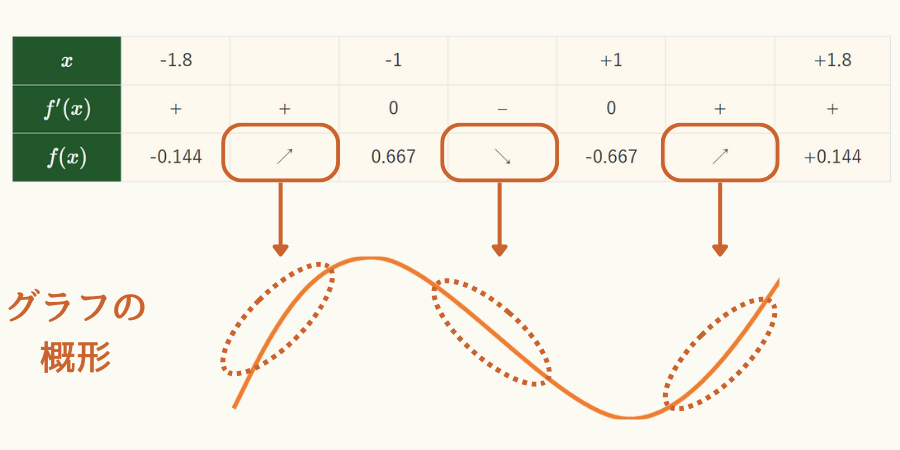
- グラフの概形
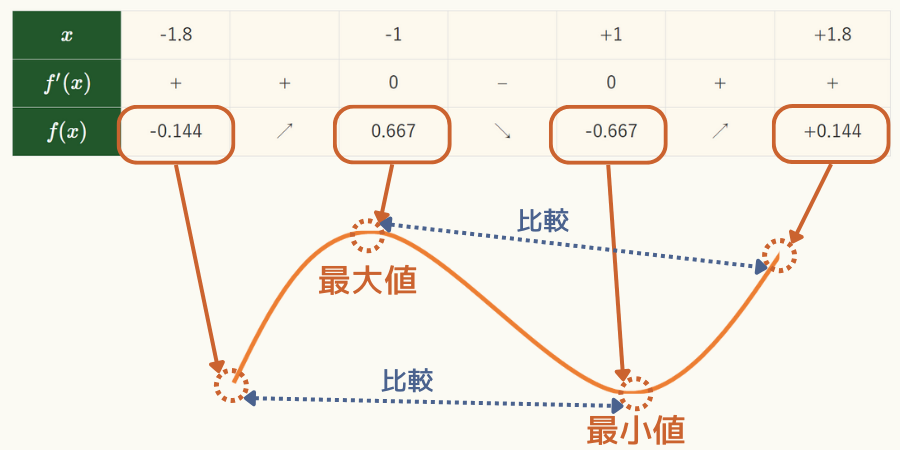
- 最大値、最小値(グラフの概形の高い所同士、低い所同士を比較)
微分値がゼロでも符号が変化しない場合(読む場合はここをクリック)
例えば、\( f(x) = x^{3} \)を考えてみます。
導関数は\( f^{\prime}(x) = 3 x^{2} \)であり、\( x = 0 \)で\( f^{\prime}(x) = 0\)となりますが、前後で符号が変化しません。
グラフ化すると下図のようになり、山頂(極大値)にも谷底(極小値)にもなっていません。
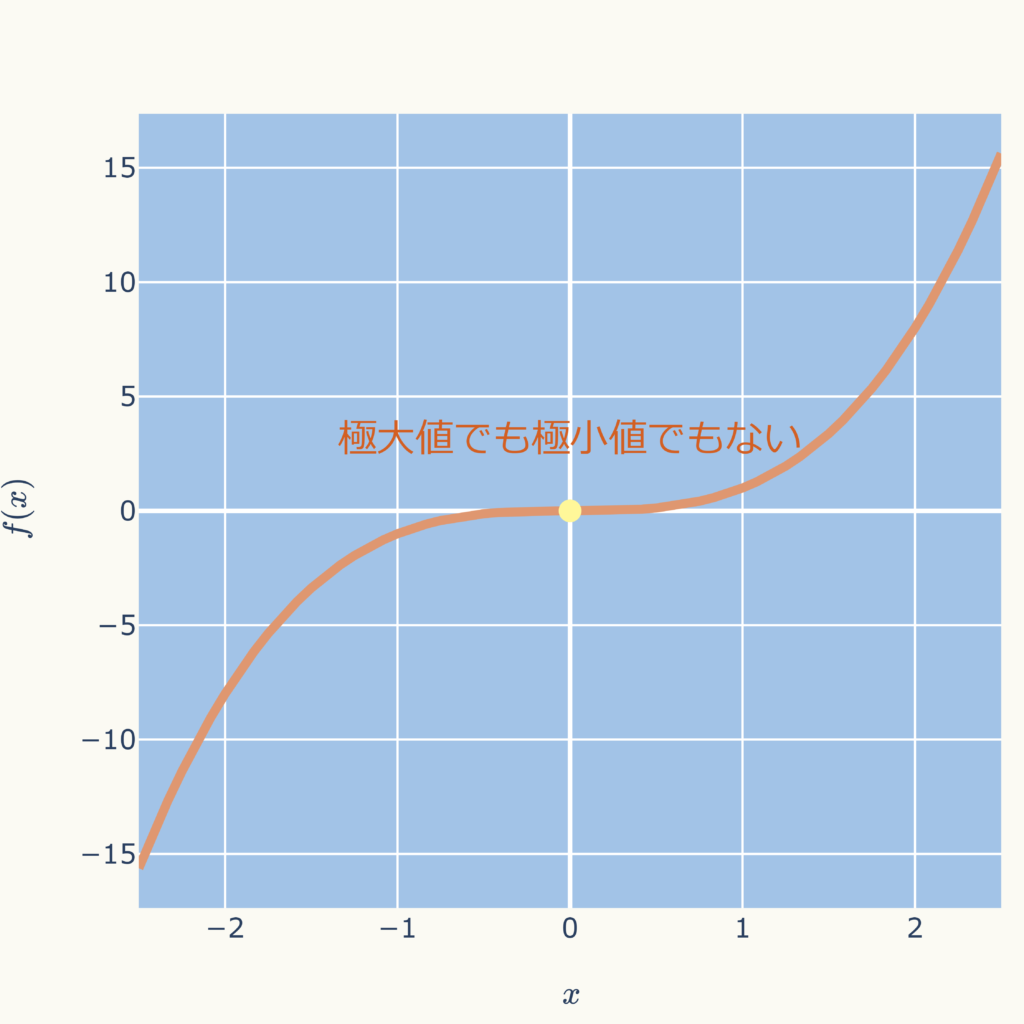
このように微分の値がゼロになっても、極大値にも極小値にもならない場合もありますので、注意が必要です。
勾配降下法(最急降下法)
概要
勾配降下法(最急降下法)は、同じような計算を反復して行うことで徐々に極小値へ近づける方法です。
例えば、下の動画のように近づいていきます。
この動画では関数\( f(x) = x^{2} \)の極小値を求めています。
計算方法
次の計算式で\( x \)の値を繰り返し更新します。
\( \hspace{10pt} \displaystyle x^{(k)} = x^{(k-1)} – \eta \frac{df(x^{(k-1)})}{dx} \)
\( \displaystyle x^{(k)} \)が更新後の\( x \)の値で、\( \displaystyle x^{(k-1)} \)は更新前の値を意味しています。
\( \displaystyle \frac{df(x^{(k-1)})}{dx} \)は微分した\( f(x) \)に\( \displaystyle x^{(k-1)} \)を代入した値です。
\( \eta \)は学習率と呼ばれ、通常小さな値を選びます。
上の動画の例では\( \eta = 0.03\)です。
\( k \)は反復回数であり、例えば1回目の計算では次式となります。
なお、\( f(x) = x^{2} \)の微分は\( \displaystyle \frac{df(x)}{dx} = 2x\)です。
\( \hspace{10pt} \displaystyle x^{(1)} = x^{(1-1)} – \eta \frac{df(x^{(1-1)})}{dx} \)
\( \hspace{20pt} \displaystyle = x^{(0)} – \eta \hspace{1pt} (2x^{(0)}) \)
\( x^{(0)} \)は\( x \)の初期値(出発点)であり、上の動画では\( x^{(0)}=7 \)としましたので、1回目の計算は
\( \hspace{10pt} \displaystyle x^{(1)} = 7 – 0.03 \times (2\times7) \)
\( \hspace{20pt} \displaystyle = 6.58 \)
になります。
これで得た\( x^{(1)} \)を使って、2回目の反復計算で\( x^{(2)} \)を求めます。
\( \hspace{10pt} \displaystyle x^{(2)} = x^{(1)} – \eta \hspace{1pt} (2x^{(1)}) \)
これを繰り返し計算していくのが勾配降下法です。
\( x^{(k)} \)が極小値へ向かう理由
\( x^{(k)} \)の更新式を見ると、\( x \)をどの方向に、どれくらい移動させるかを決めるのは\( \displaystyle -\frac{df(x^{(k-1)})}{dx} \)です。
\( -\displaystyle \frac{df(x^{(k-1)})}{dx} \)がプラスであれば、更新後の\( x^{(k)} \)は更新前の\( x^{(k-1)} \)から\( x \)がプラスの方向に、大きさが\( \displaystyle \frac{df(x^{(k-1)})}{dx} \)の絶対値に比例した分、移動することになります。
逆にマイナスであれば、\( x \)のマイナスの方向に、やはり大きさが\( \displaystyle \frac{df(x^{(k-1)})}{dx} \)の絶対値に比例した分、移動することになります。
この状況を直感的に理解するために、\( -\displaystyle \frac{df(x^{(k-1)})}{dx} \)を矢印としてグラフ上に図示したのが下図です。
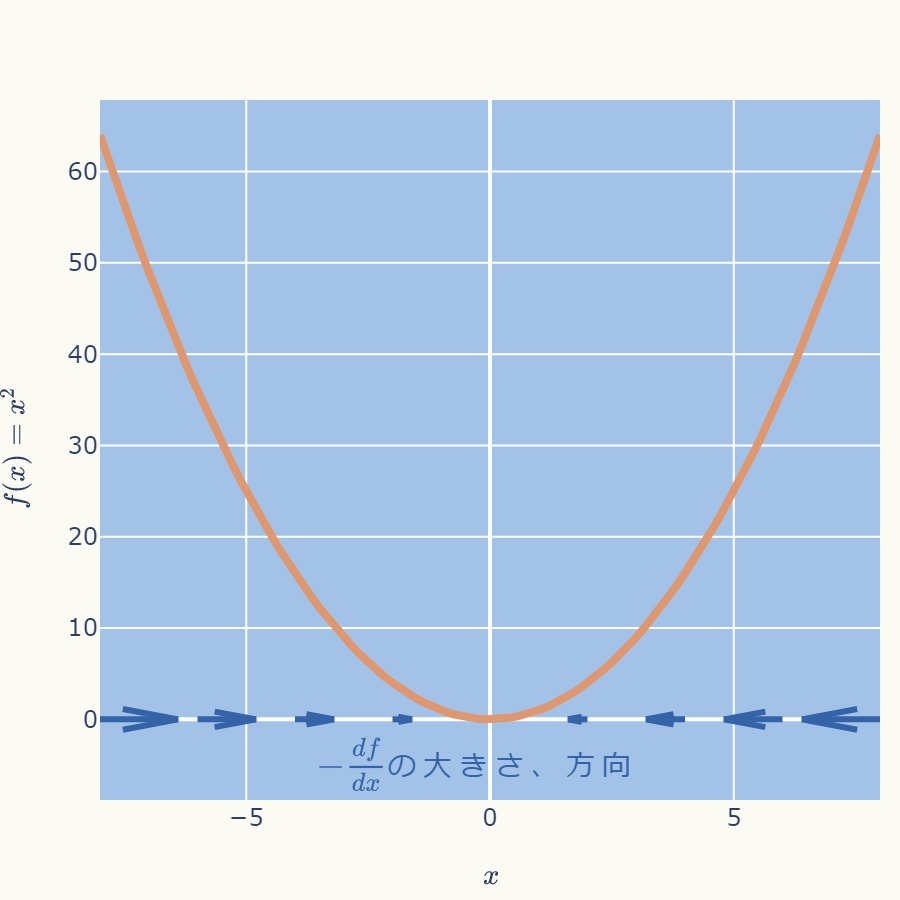
青色の矢印で、\( -\displaystyle \frac{df(x^{(k-1)})}{dx} \)がプラスであれば、矢印はプラス方向、マイナスならマイナス方向を向くように描画しています。
また、矢印の大きさは\( -\displaystyle \frac{df(x^{(k-1)})}{dx} \)の絶対値に比例した大きさです。
これを見ると、矢印は極小値を向いていることが分かります。
このため、例えば初期値が+5であろうとー5であろうと、更新式によって計算していくと極小値の\( x \)の値\( x=0 \)に向かっていくことが分かります。
また、向かう速度は矢印の大きい所、つまりグラフの傾きが大きい所で速くなることもわかります。
上の動画でも動画の最初の方の、グラフの傾きが大きい所では移動速度が速くなっていました。
例題
最大消費電力を求める
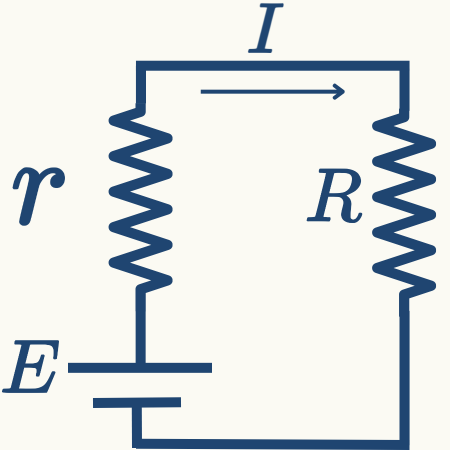
上図の電気回路において、抵抗\( R \)の消費電力\( P \)は次式となります。
\( \hspace{10pt} \displaystyle P = \frac{E^{2}}{\displaystyle R + 2r + \frac{r^{2}}{R}} \)
消費電力\( P \)が最大となる抵抗\( R \)の値は何でしょうか?
消費電力\( P \)の「分母」が最小になる時、\( P \)は最大になります。
\( \hspace{10pt} \displaystyle 分母 = R + 2r + \frac{r^{2}}{R} \)
分母を微分すると、
\( \hspace{10pt} \displaystyle \frac{d 分母}{dR} = 1 – \frac{r^{2}}{R^{2}} \)
この式は\( R=r \)の時にゼロとなり、増減表は下記になります。
| \( R \) | \( r \) | ||
| \( \displaystyle \frac{d 分母}{dR} \) | ー | 0 | + |
| \( 分母 \) | ↘ | \( 4r \) | ↗ |
このことから分母は\( R=r \)の時に最小値\( 4r \)になることがわかります。
これを消費電力\( P \)の式に代入すると、最大消費電力は
\( \hspace{10pt} \displaystyle P = \frac{E^{2}}{ 4r } \)
になります。
何に使う?
最小二乗法
最小二乗法は機械学習やAIといった分野で広く利用されている考え方です。
極大値、極小値の求め方が分かっていれば、最小二乗法の基本的な考え方も理解できます。
詳しくは、以下のページで解説しています。

