微分とは何か?
下の動画ように、微分とはグラフを直線になるまで拡大した時の傾き(変化率)を求めることです。
1枚の図としてまとめると、次になります。
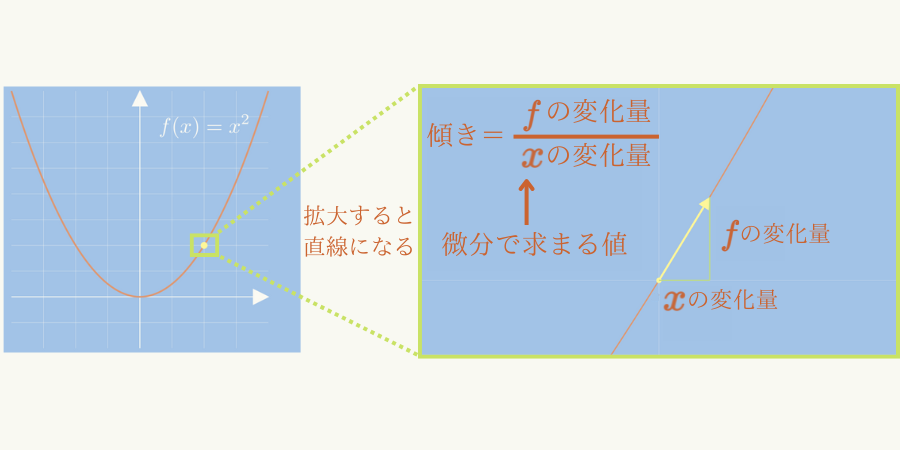
このページでは動画や図を使って、上のような微分のイメージから微分の定義式が導かれることを解説します。
その後、定義式を使った微分計算、定義式から導かれる微分の公式を使用して例題をいくつか解いていきます。
では早速、上のグラフの軸に目盛りを入れて、実際に微分の値を計算してみましょう。
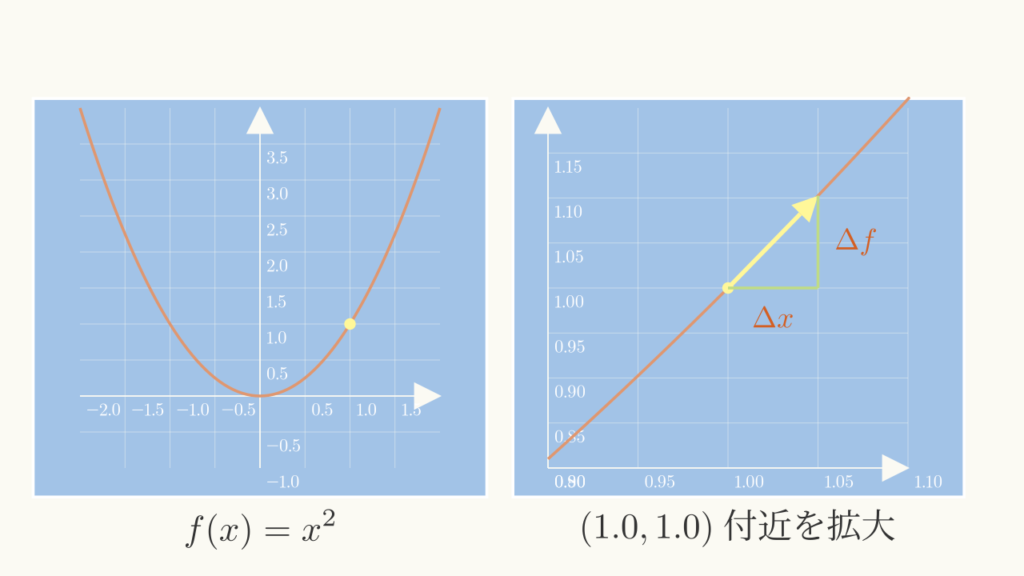
左のグラフは\( \hspace{5pt} f(x)=x^{2} \hspace{5pt} \)の\( \hspace{5pt} -2 \text{≦} x \text{≦} +2 \hspace{5pt} \)の範囲を表示したものです。
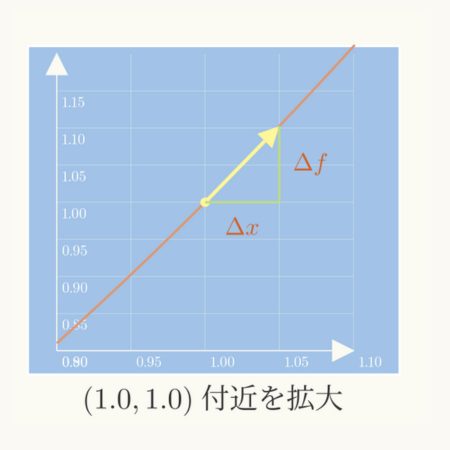
このグラフの黄色い丸の箇所\( (1.0, 1.0) \)付近を拡大したモノが、右のグラフになります。
なお、「xの変化量」を\( \Delta x \)、「fの変化量」を\( \Delta f \)で表しています。
後々、数式等でよく使用するため、記号で簡潔に表現しました。
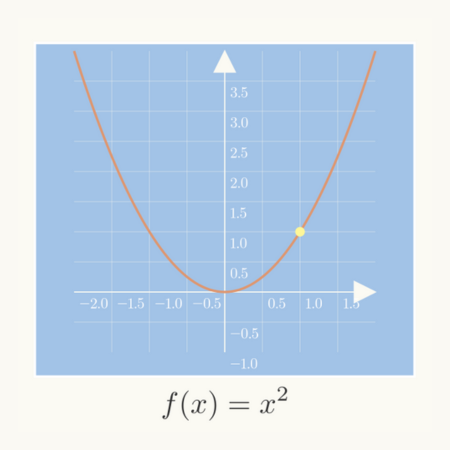
最初のグラフは\( f(x)=x^{2} \)の\( -2 \text{≦} x \text{≦} +2 \)の範囲を表示したものです。
このグラフの黄色い丸の箇所\( (1.0, 1.0) \)付近を拡大したモノが、次のグラフになります。
なお、「xの変化量」を\( \Delta x \)、「fの変化量」を\( \Delta f \)で表しています。
後々、数式等でよく使用するため記号で簡潔に表現しました。
このように\( x \)や\( f \)の小さな幅を表すのに\( \Delta \)を使用することがよくあります。
試しに、右のグラフの\( x=1と1.05\)の値を利用して、具体の変化率(傾き)を計算してみます。
試しに、このグラフの\( x=1と1.05\)の値を利用して、具体の傾き(変化率)を計算してみます。
スマホで見ている方へ。画面からはみ出る下のような式は横スクロールできます。
\( \displaystyle 傾き(変化率)= \frac{fの変化量}{xの変化量}\hspace{10pt} = \frac{\Delta f}{\Delta x} = \frac{f(1.05)-f(1)}{1.05-1} = \frac{(1.05)^{2}-(1)^{2}}{0.05} = \frac{0.1025}{0.05} = 2.05 \)
となり、\( x=1 \)における微分の理論値(学校の数学で習う微分の値)\( 2.0 \)に近い値になっています。
さらにグラフを拡大し、\( \Delta x \)を極々微小な値にする(ゼロに近づける)ことにより、微分の理論値になります。
実際、先ほどの式で\( \Delta x \)をゼロに近づけたものが後で説明する微分の定義式になります。
任意の点における微分の値
先ほどは\( x=1 \)における微分の値を求めました。
次に、下の動画のようにその他の\( x \)でも微分の値を計算し、新たな平面上にプロットするとどうなるでしょうか。
\( f^{\prime}(x) = 2x \)上の点になります。
\( f^{\prime}(x) = 2x \)は後で説明する微分の定義式を使って、\( f(x) = x^2 \)から求めることができます。
微分の定義式において、実際に\( f^{\prime}(x) = 2x \)を導出しています。
数式を得ることで、任意の点における厳密な微分値を得ることが可能となります。
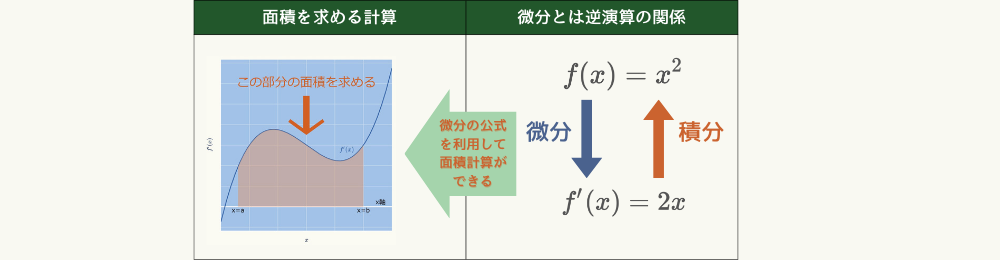
このイメージのメリット
微分の説明の仕方にはいくつかあります。
代表的な説明は「グラフの特定の点における接線の傾き」だと思います。
しかし、ここではあえて「微分とはグラフを直線になるまで拡大した時の傾き(変化率)を求めること」としています。
その理由は、この説明に暗に隠れている次の考え方が数学や物理学を理解する上で有用だからです。
曲線のグラフも微小な直線の連続とみなせる
例えば、積分は微分と逆演算の関係(ある関数を微分して、積分すると元にもどる関係)にあります。
これを微分積分学の基本定理といいますが、これも曲線のグラフも微小な直線の連続とみなせることを利用して、次の動画のように説明することができます。
詳しくは積分の基礎で説明しています。
微分の定義式
関数\( f(x) \)の微分\( f^{\prime}(x) \)の定義式は次のとおりです。
$$ \displaystyle f^{\prime}(x) = \lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) – f(x)}{\Delta x} $$

これは基本的に、「微分とは何か?」の\( \hspace{3pt} \displaystyle 傾き(変化率)= \frac{\Delta f}{\Delta x} \hspace{3pt} \)において、\( \Delta x \)をゼロに近づけただけです。
定義式の説明
「微分とは何か?」で書いたように、変化率(傾き)の計算式\( \displaystyle \frac{\Delta f}{\Delta x} \)の\( \Delta x \)を極々微小な値にする(ゼロに近づける)ことにより、微分の理論値(定義式)になります。
これを数式で表現すると、点\( x=a \)における微分の理論値を\( f^{\prime}(a) \)と表記した場合、
\( \hspace{30pt} \displaystyle f^{\prime}(a) = 傾き(変化率)=\lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x}\)
です。
(「微分とは何か?」の例では\( a=1 \)でした)
\( \Delta f = f(a+\Delta x) – f(a) \)であることから、次式となります。
\( \hspace{30pt} \displaystyle f^{\prime}(a) = \lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(a+\Delta x) – f(a)}{\Delta x} \)
この式の\( a \)を\( x \)に置き換え、任意の点\( x \)における式に変えると、上記の定義式になります。
\( \hspace{30pt} \displaystyle f^{\prime}(x) = \lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) – f(x)}{\Delta x} \)

この式を利用して、関数\( f(x) \)の任意の点\( x \)における極々微小な直線の変化率(傾き)を求めることができます。
具体例として、「微分とは何か?」で使用した\( f(x) = x^{2} \)を定義式を使用して微分すると
\( \hspace{30pt} \displaystyle f^{\prime}(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) – f(x)}{\Delta x} \)
\( \hspace{50pt} \displaystyle = \lim_{\Delta x \to 0} \frac{(x+\Delta x)^{2} – x^{2}}{\Delta x} \)
\( \hspace{50pt} \displaystyle = \lim_{\Delta x \to 0} \frac{x^{2} + 2 x \Delta x + \Delta x^{2} – x^{2}}{\Delta x}\)
\( \hspace{50pt} \displaystyle = \lim_{\Delta x \to 0} \frac{2 x \Delta x + \Delta x^{2}}{\Delta x} \)
\( \hspace{50pt} \displaystyle = \lim_{\Delta x \to 0} (2 x + \Delta x) \)
\( \hspace{50pt} \displaystyle = 2 x \)
となり、\( x=1 \)の時は、\( f^{\prime}(1) = 2 \)となります。これが「微分とは何か?」で述べた微分の理論値です。
ちなみに、今回は微分の定義式を理解する目的もあって、定義式を直接使って計算しましたが、通常は定義式から導かれた次のような微分の公式
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)
を利用して微分を計算します。
このページの「公式集」に公式を掲載しています。
微分の公式を使用した微分計算については「例題」をご覧ください。
微分記号
微分の記号は複数の表現があります。よく使われる表記法を次に示します。
\( \hspace{30pt} \displaystyle f^{\prime}(x) = \frac{df}{dx} = \frac{df(x)}{dx} = f^{(1)}(x) \)
\( \hspace{30pt} \displaystyle f^{\prime\prime}(x) = \frac{d^{2}f}{dx^{2}} = \frac{d^{2}f(x)}{dx^{2}} = f^{(2)}(x) \)
\( \hspace{30pt} \displaystyle f^{\prime\prime\prime}(x) = \frac{d^{3}f}{dx^{3}} = \frac{d^{3}f(x)}{dx^{3}} = f^{(3)}(x) \)
ここで、\( f^{\prime\prime}(x) \)は\( f^{\prime}(x) \)をさらに微分した場合であり(2階微分と言います)、\( f^{\prime\prime\prime}(x) \)は\( f^{\prime\prime}(x) \)をさらに微分した場合です(3階微分と言います)。
ちなみに、\( f^{(0)}(a) = f(x)\)です。
\( df \)や\( dx \)の意味?
微分 を\( \displaystyle \frac{df}{dx} \)と表記し、分数のように扱う場合もあります。実際、
$$ f^{\prime}(x) = \frac{df}{dx} = \lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} $$
であることから、\( dx \)は極々微小な値であり、\( df \)は\( x \)をその\( dx \)分だけ変化させた時の変化分と考えることができます。
導関数、微分係数とは
導関数とは\( f^{\prime}(x) \)のことで、その名の通り「関数」になってまして、変数\( x \)に値を代入することで、任意の点の微分を求める事ができます。
一方、微分係数は\( f^{\prime}(a) \)のことで、\( x=a \)における具体の「値」になります。
上記の\( f(x) = x^{2} \)の例ですと、\( f^{\prime}(x) = 2x\)が導関数で、\( f^{\prime}(1) = 2 \)は微分係数です。
グラフを拡大すると直線になる理由
次式のように、関数を多項式に変換するテイラー展開という手法があります。
\( \hspace{30pt} \displaystyle f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^{n} \)
\( \hspace{50pt} \displaystyle = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime\prime}(a)}{2!}(x-a)^{2} + \frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^{3} + \cdots \)
たいていの関数に使用でき、例えば\( f(x) = \sin(x),a=0\)は次のように変換されます。
\( \hspace{30pt} f(x) = \sin(x) = x – \frac{x^{3}}{3!} + \frac{x^{5}}{5!}+ \cdots \)
「微分とは何か?」で使用した\( f(x) = x^{2} \)は元々多項式ですが、テイラー展開すると次式へ変形されます。
\( \hspace{30pt} f(x) = f(a) + 2a(x-a) + \frac{2(x-a)^{2}}{2!} \)
この式において\( \Delta x = x-a \)とすると、次式になります。(「微分とは何か?」は、\( a = 1 \)の場合です。)
\( \hspace{30pt} f( a + \Delta x ) = f(a) + 2a( \Delta x ) + \frac{2( \Delta x )^{2}}{2!} \)
さらに右辺の\( f( a ) \)を左辺へ移項して、\( \Delta f = f( a + \Delta x ) – f( a ) \)とすると、
\( \hspace{30pt} \Delta f = 2a( \Delta x ) + \frac{2( \Delta x )^{2}}{2!} \)
となります。
この式で\( \Delta x \) を小さくすれば(つまり、\( x \)を\( a \)に近づければ)、右辺の第二項は\( \Delta x^{2} \)を持つので、第一項に比べて無視できるほど小さくすることができ、次式に近似できます。(例えば\( \Delta x = 0.01 \)なら、\( \Delta x^{2} \)は\( \Delta x \)に比べて百分の一になります。)
\( \hspace{30pt} \Delta f \simeq 2a( \Delta x ) \)
この式で\( \Delta f \)は\( \Delta x \) の一次関数であり、直線になることが分かります。
同様の考えをテイラー展開の公式に適用すると、
\( \hspace{30pt} \displaystyle \Delta f = f^{\prime}(a)\Delta x + \frac{f^{\prime\prime}(a)}{2!}\Delta x^{2} + \frac{f^{\prime\prime\prime}(a)}{3!}\Delta x^{3} + \cdots \)
において、\( f^{\prime\prime}(a) \)、\( f^{\prime\prime\prime}(a) \)などが極端に大きくなる場合を除き、\( \Delta x \) を小さくすることにより、
\( \hspace{30pt} \Delta f \simeq f^{\prime}(a)\Delta x \)
となり、やはり直線になることが分かります。
例題
関数\( f(x) = 2x^{3} – 5x^{2} + 3x – 7 \)を微分してください。
次のべき関数の微分の公式を使用します。
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)
これを使用すると\( x^{3} \)は\( n=3 \)ですので、
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{3} = 3 x^{2} \)
同様に
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{2} = 2 x \)
\( \hspace{10pt} \displaystyle \frac{d}{dx} x = x^{0} = 1 \)
になります。
また、定数の微分の公式
\( \hspace{10pt} \displaystyle \frac{d}{dx}( c ) = 0 \)
より、定数の微分はゼロになります。
以上を使えば、例題の関数の微分は
\( \hspace{10pt} \displaystyle f^{\prime}(x) = 2(3x^{2}) – 5(2x) + 3 \)
\( \hspace{20pt} \displaystyle f^{\prime}(x) = 6x^{2} – 10x + 3 \)
となります。
下の動画の左図のようにボールが自由落下する場合を考えます。
落下距離\( h[m] \)の関数は時間\( t[s] \)を使用して、次式になります。
\( \hspace{30pt} \displaystyle h(t) = -\frac{1}{2} g t^{2} \hspace{10pt} (ここで、g = 9.8 [m/s^{2}](重力加速度))\)
この式より、落下開始から2秒後(\( t=2 \))のボールの速度を求めてください。
なお、この式を使用して、時間と落下距離の関係をグラフ化したモノが中央のグラフです。
さらに\( t=2 \)付近を拡大したモノが右のグラフです。
上で見たように、微分はグラフの微小な範囲で変化率を求める計算ですので、微分の定義式
\( \hspace{30pt} \displaystyle 微分=変化率=\lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} \)
において、\( \Delta f \)⇒\( \Delta h \):「落下距離\( h[m] \)の変化量」、\( \Delta x \)⇒\( \Delta t \):「時間\( t[s] \)の変化量」とします。
こうすることで、落下距離の時間変化率、つまり落下速度を求める事ができます。
\( \hspace{30pt} \displaystyle 落下速度[m/s] = \lim_{\Delta t \to 0} \frac{h(t+\Delta t) – h(t)}{\Delta t} = h^{\prime}(t)\)
となり、これは関数\( h(t) \)の微分です。
微分の公式
\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)
から、
\( \hspace{10pt} \displaystyle \frac{d}{dt} t^{2} = 2 t \)
となりますので、
\( \hspace{30pt} \displaystyle h^{\prime}(t) = -\frac{1}{2} g (2t) \)
\( \hspace{50pt} \displaystyle = -gt \)
これが任意の時刻\( t \)におけるボールの速度の計算式です。
\( t = 2 \) の場合は\( -9.8 \times 2 = -19.6[m/s] \)となります。
何に使う?
最大値、最小値の探索
微分は誤差を最小にする、消費電力を最小にするなど、関数の最大値、最小値を見つけるために利用することができます。
このことが微分の応用範囲を多方面へ広げました。
微分を利用した最大値、最小値の探索方法、使用例については「極大値、極小値」のページで解説しています。
積分の計算
積分は関数が描く面積を求める計算ですが、その計算を微分の公式を利用して行うことができます。
積分については下のページをご覧ください。
公式集
基本
- 定数の微分 \( \hspace{5pt} \displaystyle \frac{d}{dx}( c ) = 0 \)
- 和の微分 \( \hspace{5pt} \displaystyle \frac{d}{dx} \Bigl( a f(x) + b g(x) \Bigr) = a \frac{df(x)}{dx} + b \frac{dg(x)}{dx} \)
- 積の微分 \( \hspace{5pt} \displaystyle \frac{d}{dx} \Bigl( f(x) g(x) \Bigl) =\frac{df(x)}{dx} g(x) + f(x) \frac{dg(x)}{dx} \)
- 商の微分(分数の微分) \( \hspace{5pt} \displaystyle \frac{d}{dx} \Biggl( \frac{f(x)}{g(x)} \Biggl) =\frac{\frac{df(x)}{dx} g(x) – f(x) \frac{dg(x)}{dx}}{(g(x))^{2}} \)
- 合成関数の微分(連鎖律) \( \hspace{5pt} \displaystyle \frac{d}{dx} f \bigl( g(x) \bigr) =\frac{df}{dg} \frac{dg}{dx} \)
べき関数の微分
- \( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)
指数関数の微分
- \( \hspace{10pt} \displaystyle \frac{d}{dx} a^{x} = a^{x} \log a \)
- \( \hspace{10pt} \displaystyle \frac{d}{dx} e^{x} = e^{x} \)
対数関数の微分
- \( \hspace{10pt} \displaystyle \frac{d}{dx} \log{_a} x = \frac{1}{x \log a} \)
- \( \hspace{10pt} \displaystyle \frac{d}{dx} \log |x| = \frac{1}{x} \)
三角関数の微分
- \( \hspace{10pt} \displaystyle \frac{d}{dx} \sin x = \cos x \)
- \( \hspace{10pt} \displaystyle \frac{d}{dx} \cos x = -\sin x \)
- \( \hspace{10pt} \displaystyle \frac{d}{dx} \tan x = \frac{1}{\cos^{2} x} \)