積分の基礎

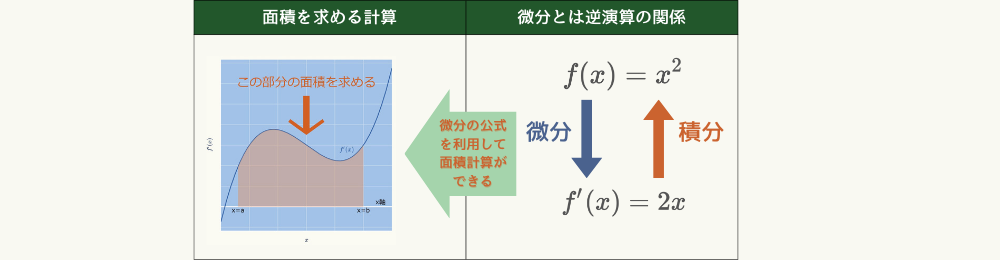
積分とは何か？

積分とは、関数が描く曲線とx軸で囲まれた面積を求める計算であり、また、微分とは逆演算の関係にあります。

逆演算とは、ある関数を微分して、その結果を積分すると元の関数に戻る関係のことです。

このことから、微分の公式（\( \hspace{10pt} \frac{d}{dx} x^{n} = n x^{n-1} \)など）を利用して面積計算を行うことができます。

これが積分の最も重要な事柄です。

このページでは動画や図を多く使って、なぜ積分は面積計算なのか？、なぜ微分と積分が逆演算になるのか？を分かりやすく解説します。

そして微分の公式を利用した積分計算を説明し、例題をいくつか解いていきます。

なぜ積分は面積計算なのか？

積分が面積計算となる理由は、積分が下の動画のように微小な長方形の面積を足していくことで面積を求める計算だからです。

具体の計算手順を見てみましょう。

下図のように、最初の長方形の高さは\( f^{\prime}(a ) \)、幅は\( \Delta x \)になります。

なお、動画では「ｘの変化量」としていましたが、今後、計算式で何度も出てくるため、記号で\( \Delta x \)と簡潔に表しました。

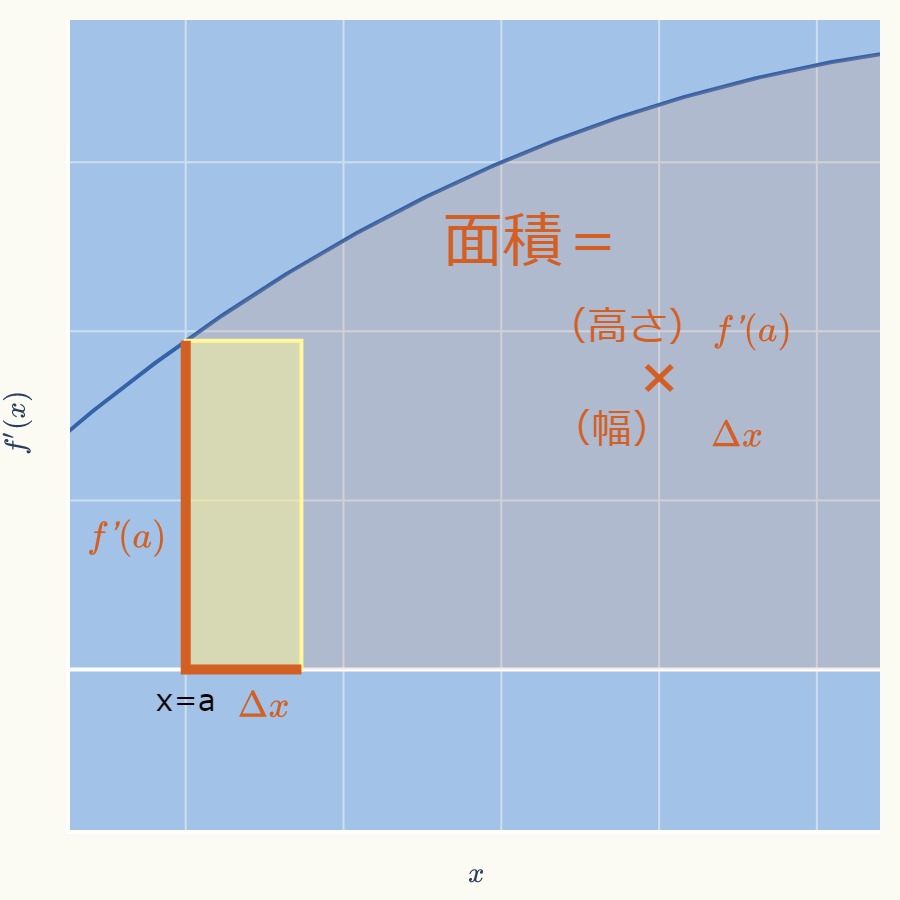
よって、最初の長方形の面積は\( f^{\prime}(a ) \Delta x \)となります。

次の長方形は幅\( \Delta x \)は変わらず、高さは\( \Delta x \)だけズレた\( f^{\prime}(a + \Delta x) \)の値になりますので、\( f^{\prime}(a + \Delta x) \Delta x \)となります。

このような微小な長方形の面積を足していく計算式は以下のようになります。

スマホでご覧の方へ、画面からはみ出てしまうような下のような数式はスクロールできます。

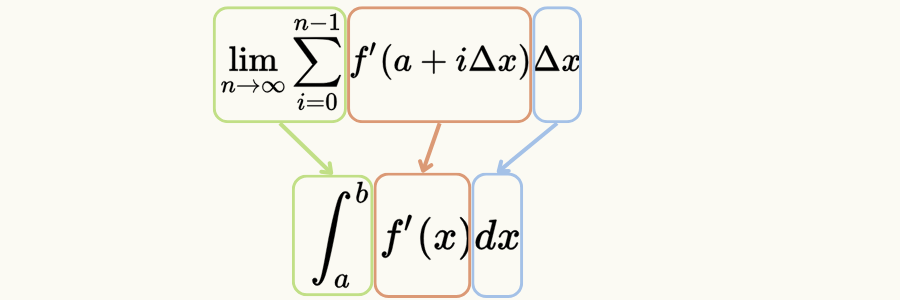
\( \hspace{10pt} \displaystyle 微小な長方形の和 = f^{\prime}(a) \Delta x \hspace{5pt}+\hspace{5pt} f^{\prime}(a + \Delta x) \Delta x \hspace{5pt}+\hspace{5pt} f^{\prime}(a + 2 \Delta x) \Delta x \hspace{5pt} \cdots \)

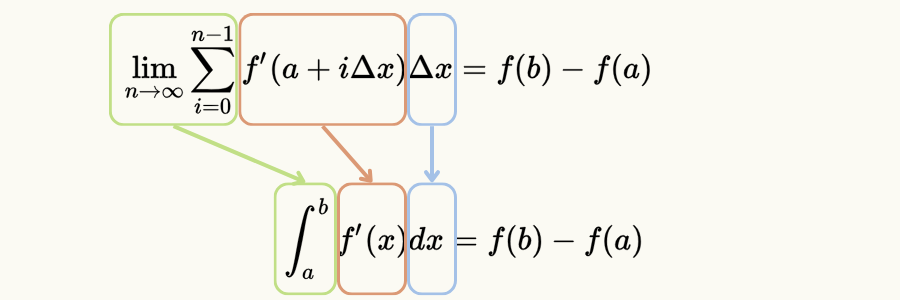
\( \hspace{70pt} \displaystyle = \sum_{i=0}^{n-1} f^{\prime}(a + i \Delta x) \Delta x \)

\( \hspace{70pt} \displaystyle \left( ここで、 \Delta x = \frac{b-a}{n} \right) \)

\( \hspace{70pt} \displaystyle \simeq 求める面積 \)

先の動画は、\( f^{\prime}(x) = (x – 2) (x – 3) (x – 4) + 1.5 \)、\( a = 1.8 \)、\( b = 4.0 \)、\( n = 30 \)の場合でして、計算される面積は約3.27です。

これは、「微分の公式を使った積分計算」で説明する積分の理論値（正確な面積）3.2516に近い値になっています。

\( n \)の値を大きくし、より細かい長方形にすることで、理論値（正確な面積）に近づきます。

実際、\( n \to \infty \)とした場合が積分の定義式となります。

積分の定義式

積分の定義式は次の通りです。なお、\( \int \)はインテグラルと読み、積分を表す記号です。

$$ \displaystyle \int_{a}^{b} f^{\prime}(x)dx = \lim_{n \to \infty } \sum_{i=0}^{n-1} f^{\prime}(a + i \Delta x) \Delta x $$
$$ \displaystyle \left( ここで、 \Delta x = \frac{b-a}{n} \right) $$

これは先程の「微小な長方形の和」の計算式において、\( \displaystyle \lim_{n \to \infty } \)として積分の表記法\( \int \)や\( dx \)で表しただけです。

ちなみに、折角の定義式ですが、この\( \sum \)や\( \lim \)の計算を直接行うことはまず無いと思います。

その理由は、次に説明する微分積分学の基本定理により、微分と積分が逆演算であることが示されたので、通常はそれを利用して積分の計算をするためです。

なぜ微分と積分が逆演算になるのか？

微分の公式を使って積分計算ができる事実（「微分積分学の基本定理」と言います）のみ知っていれば、およそ問題なく積分計算ができます。
ですので、より突っ込んで微分と積分が逆演算になる理由を知りたい方だけこの項目をご覧いただければと思います。
そうではなく具体の積分の計算ができれば十分という場合は、この項目を飛ばして次の「微分積分学の基本定理（微分と積分は逆演算の定理）」に進んでいただいても問題ありません。

下の動画のように「微分とはグラフを直線になるまで拡大した時の傾き（変化率）を求めること」です。

（微分について詳しく知りたい方は「微分の基礎」のページをご覧ください）

「グラフを直線になるまで拡大」ということは、それは逆に見れば、曲線のグラフも微小な直線の連続とみなせる、ということです。

つまり、曲線のグラフも微小な直線の連続であり、微分とはその微小な直線の傾き（変化率）を求めること、です。

下の動画は\( \hspace{5pt} f(x)=x^{2} \hspace{5pt} \)の\( \hspace{5pt} -4 \text{≦} x \text{≦} +4 \hspace{5pt} \)の微小な直線の傾きをプロットすることで\( \hspace{5pt} -4 \text{≦} x \text{≦} +4 \hspace{5pt} \)の「微分の値」のグラフを描画しています。

このことから、逆に「微分の値」が分かっていれば、つまり微小な直線の傾きが分かっていれば、その微小な直線をつなげることにより、微分前の関数（上の動画だと\( \hspace{5pt} f(x)=x^{2} \hspace{5pt} \)です）のグラフを再構成することができます。

実際に、積分の計算は下の動画のように、微小な直線をつないでいく（微小な直線の変化量を足していく）ことにより、微分前の関数の変化量を計算すること、と考えることもできます。

この動画では例として微分前の関数は\( f(x) = x^{2} \)、それを微分した、微分後の関数は\( f^{\prime}(x) = 2x \)を使用しています。

具体の計算手順を見てみましょう。

最初の微小な直線は下図のように傾きは\( f^{\prime}(a )\)であり、\( x \)の変化量は\( \Delta x \)です。

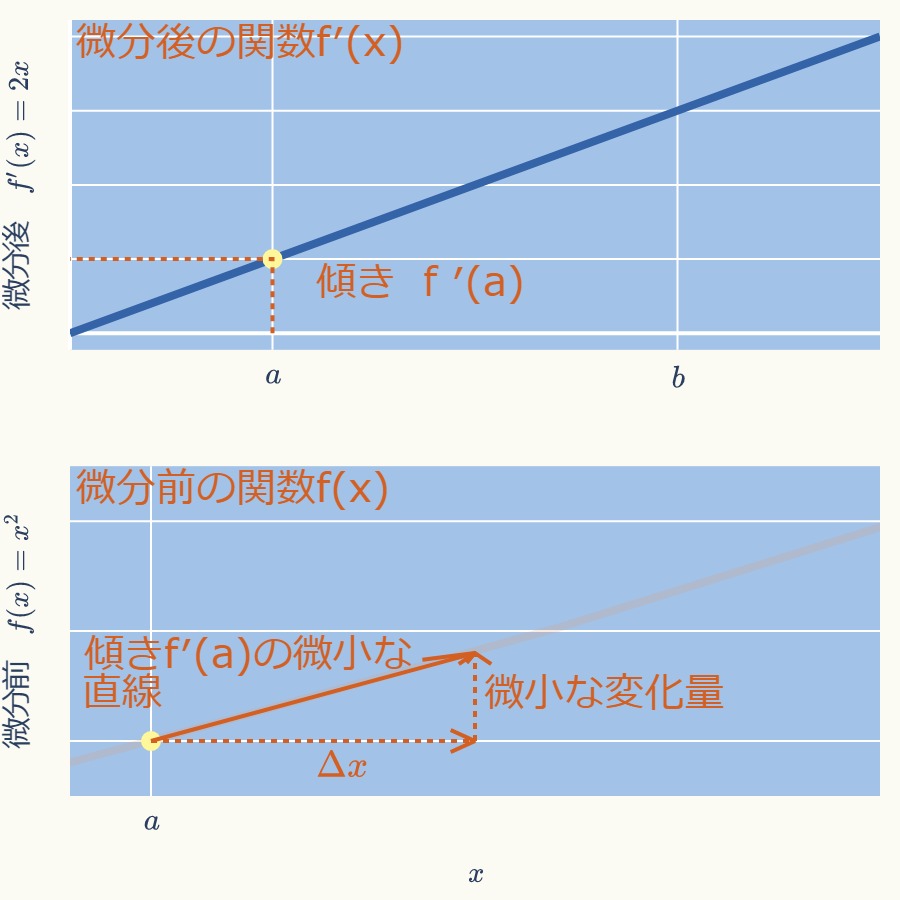
このため「微小な変化量」は、\( f^{\prime}(a ) \Delta x \)となります。

なお、動画では「ｘの変化量」としていましたが、今後、計算式で何度も出てくるため、記号で\( \Delta x \)と簡潔に表しました。

次の直線による変化量は\( \Delta x \)は変わらず、一方、傾きの値は\( \Delta x \)だけズレた\( f^{\prime}(a + \Delta x) \)の値になりますので、\( f^{\prime}(a + \Delta x) \Delta x \)となります。

このような微小な直線による変化量を足していく計算式は以下のようになります。

\( \hspace{10pt} \displaystyle 微小な変化量の和 = f^{\prime}(a ) \Delta x \hspace{5pt}+\hspace{5pt} f^{\prime}(a + \Delta x) \Delta x \hspace{5pt}+\hspace{5pt} f^{\prime}(a + 2 \Delta x) \Delta x \hspace{5pt} \cdots \)

\( \hspace{70pt} \displaystyle = \sum_{i=0}^{n-1} f^{\prime}(a + i \Delta x) \Delta x \)

\( \hspace{70pt} \displaystyle \left( ここで、 \Delta x = \frac{b-a}{n} \right) \)

\( \hspace{70pt} \displaystyle \simeq f(b)-f(a) \)

当然ですが、同じ積分の計算ですので、計算式上は「なぜ積分は面積計算なのか？」と同じになります。

違いは\( f^{\prime}(x) \)を長方形の縦の長さと考えるか、微小な直線の傾きと考えるか、その捉え方だけです。

また、この動画で微分後の関数\( f^{\prime}(x) \)を使用して、微分前の関数\( f(x) \)を再構成できることが分かると思います。

つまり、積分は微分の逆演算の関係になります。

ちなみに、先の動画は、\( f^{\prime}(x) =2x \)、\( f(x) =x^{2} \)、\( a = 1 \)、\( b = 3 \)、\( n = 50 \)の場合でして、この微小な直線の積み重ねで求まる変化量\( f(b) – f(a) \)は7.92です。

これは、\( f(x) =x^{2} \)を利用した計算値（理論値）\( f(3) – f(1) = 3^{2} – 1^{2} = 9-1=8 \)に近い値になっています。

\( n \)の値を大きくすることで、理論値に近づきます。

実際、\( n \to \infty \)とした場合が微分と積分が逆演算であることを示す微分積分学の基本定理となります。

微分積分学の基本定理（微分と積分は逆演算の定理）

微分積分学の基本定理とは、微分と積分が逆演算の関係にあることを表すもので、次式となります。

$$ \displaystyle \int_{a}^{b} f^{\prime}(x)dx = f(b) – f(a) $$

ただし、\( f^{\prime}(x) \)は\( f(x) \)を微分した関数です。

この式は言い換えれば、区間\( [a,b] \)において関数\( f^{\prime}(x) \)が描くグラフとx軸で囲まれた面積を求めたければ、微分前の関数\( f(x) \)を使って、\( f(b) – f(a) \)を計算すればよい、ということです。

なお、この式は「なぜ微分と積分が逆演算になるのか？」で出てきた「微小な変化量の和」の計算式において、\( \displaystyle \lim_{n \to \infty } \)として、「積分の定義式」の積分の表記法\( \int \)や\( dx \)で書き換えただけです。

この定理が発見されたことで、「積分の定義式」の数式を真正面から計算しなくても、微分前と微分後の関数を知っていれば（微分の公式を知っていれば）積分計算を行うことができるようになりました。

微分の公式を使った積分計算

例えば「なぜ積分は面積計算なのか？」の例の場合、

\( \hspace{10pt} \displaystyle f^{\prime}(x) = (x – 2) (x – 3) (x – 4) + 1.5 \)

\( \hspace{30pt} \displaystyle = x^{3} -9x^{2}+26x-\frac{45}{2} \)

でした。

例えば、この式の中の\( x^{3} \)の場合、べき関数の微分の公式

\( \hspace{10pt} \displaystyle \frac{d}{dx} x^{n} = n x^{n-1} \)

を両辺\( n \)で割り

\( \hspace{10pt} \displaystyle \frac{d}{dx} \frac{1}{n}x^{n} = x^{n-1} \)

であることから、\( n – 1 = 3 \)の場合、\( n = 4 \)なので、

\( \hspace{10pt} \displaystyle \frac{d}{dx} \frac{1}{4}x^{4} = x^{3} \)

となり、微分前は\( \frac{1}{4}x^{4} \)であることがわかります。

同様に行えば、微分前の関数は次になります。

\( \hspace{10pt} \displaystyle f(x) = \frac{1}{4}x^{4} -9\left(\frac{1}{3}x^{3}\right)+26\left(\frac{1}{2}x^{2}\right)-\frac{45}{2}\left(x\right) +c \)

\( \hspace{20pt} \displaystyle = \frac{1}{4}x^{4} -3x^{3}+13x^{2}-\frac{45}{2}x +c \)

定数\( c \)が入ってくることに注意しましょう。

定数を微分するとゼロ\( \frac{d}{dx} (c) = 0 \)になるため、微分前の定数の値は分からなくなってしまいます。

このため、具体の値は分からないけれど定数が存在する可能性を示すため、\( c \)を入れます。

なお、すぐ下の計算で分かりますが、積分で具体の値を計算すると\( c \)は打ち消しあって消えます。

\( a = 1.8 \)、\( b = 4.0 \)でしたので、積分は

\( \hspace{10pt} \displaystyle \int_{a}^{b} f^{\prime}(x)dx = f(4)-f(1.8) \)

\( \hspace{50pt} \displaystyle = \Bigl\{ \frac{1}{4}(4.0)^{4} -3(4.0)^{3}+13(4.0)^{2}-\frac{45}{2}(4.0) +c \Bigl\} \)

\( \hspace{70pt} \displaystyle -\Bigl\{ \frac{1}{4}(1.8)^{4} -3(1.8)^{3}+13(1.8)^{2}-\frac{45}{2}(1.8) +c \Bigl\}\)

\( \hspace{50pt} \displaystyle = 3.2516 \)

これが「なぜ積分は面積計算なのか？」で述べた積分の理論値です。

定積分、不定積分とは？

定積分とは\( \displaystyle \int_{a}^{b} f^{\prime}(x)dx \)のことであり、具体の「数値」を求める積分です。

上の例では\( \displaystyle \int_{1.8}^{4} f^{\prime}(x)dx = 3.2516 \)でした。

不定積分は\( \displaystyle \int f^{\prime}(x)dx = f(x) \)で表し、微分前の「関数」を求める積分です。

上の例では

\( \displaystyle f(x) = \frac{1}{4}x^{4} -3x^{3}+13x^{2}-\frac{45}{2}x +c \)

が関数\( f^{\prime}(x) \)の不定積分です。

定積分の記号\( \displaystyle \left[ f(x) \right]_{a}^{b} \)

定積分は記号を使って次のように書くのが通例です。

\( \hspace{10pt} \displaystyle \int_{a}^{b} f^{\prime}(x)dx = f(b) – f(a) = \left[ f(x) \right]_{a}^{b} \)

例えば上の例では、

\( \hspace{10pt} \displaystyle \int_{a}^{b} f^{\prime}(x)dx = f(4)-f(1.8) \)

\( \hspace{50pt} \displaystyle = \left[ \frac{1}{4}x^{4} -3x^{3}+13x^{2}-\frac{45}{2}x +c \right]_{1.8}^{4.0} \)

と表現します。

例題

負の面積

積分は\( f^{\prime}(x) \Delta x \)を足していくことですので、\(x\)軸より下は\( f^{\prime}(x)\)が負になるため、面積も負の値になります。

結果かから言うと、この例題は下図のようにｘ軸より上の正の面積と負の面積が同じため、積分はゼロになります。

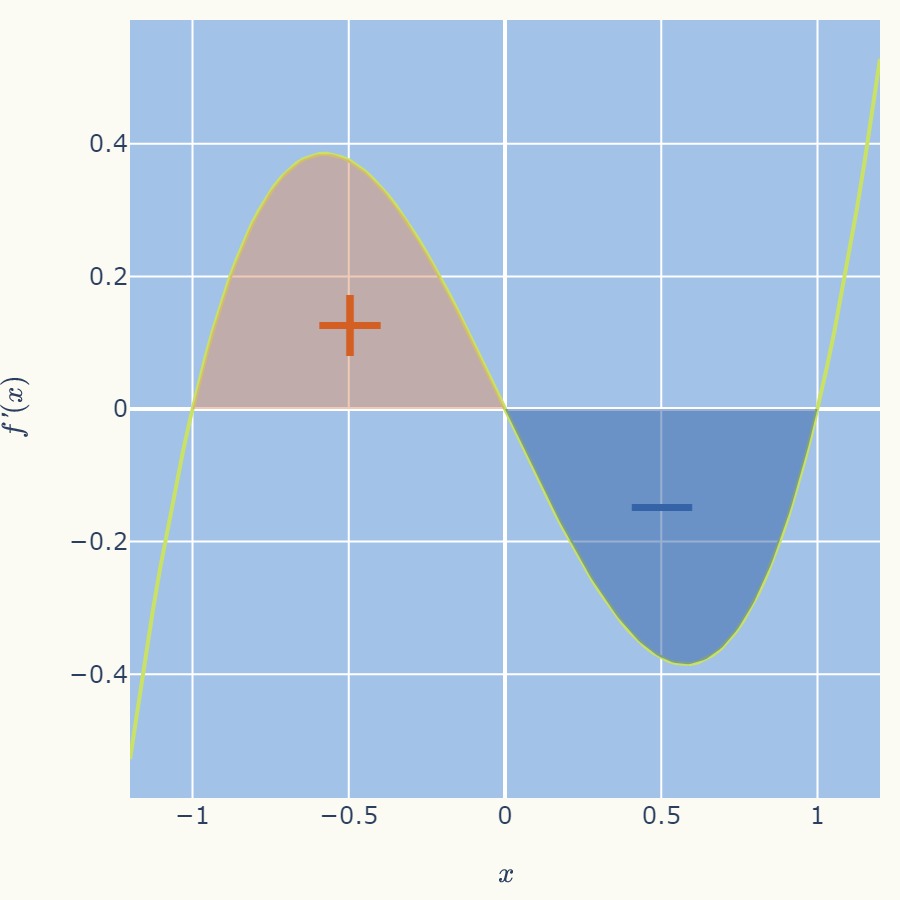
具体に計算してみましょう。

\( \hspace{10pt} \displaystyle f^{\prime}(x) = x (x – 1) (x + 1)\)

\( \hspace{50pt} \displaystyle = x^{3} – x\)

の不定積分は

\( \hspace{10pt} \displaystyle f(x) = \frac{x^{4}}{4}-\frac{x^{2}}{2} +c\)

となります。よって、

\( \hspace{10pt} \displaystyle \int_{a}^{b} f^{\prime}(x)dx = \left[ \frac{x^{4}}{4}-\frac{x^{2}}{2} +c \right]_{-1.0}^{+1.0} \)

\( \hspace{50pt} \displaystyle = 0 \)

走行距離の計算

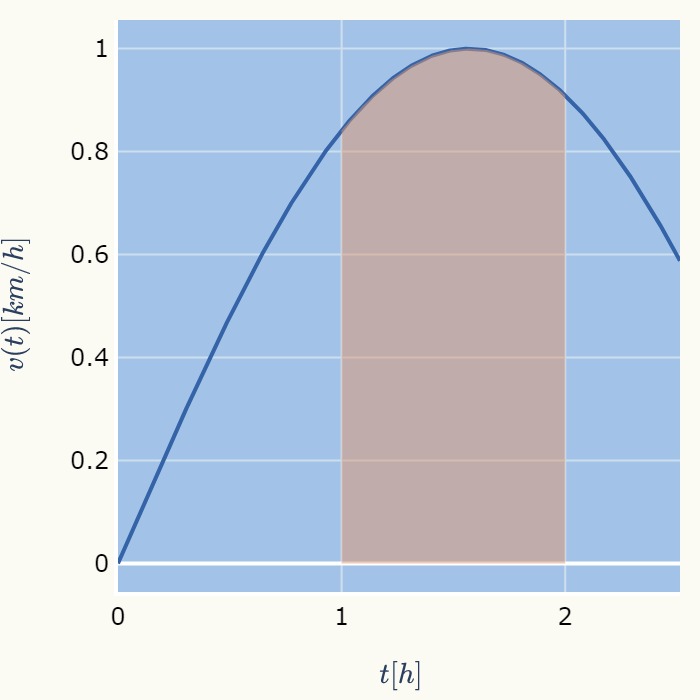
これは「微分積分学の基本定理」

\( \hspace{10pt} \displaystyle \int_{a}^{b} f^{\prime}(x)dx = f(b) – f(a) \)

において、\( a=1 \)、\( b=2 \)、\( f^{\prime}(x)⇒v(t) \)であり、

\( \hspace{10pt} \displaystyle \int_{1}^{2} v(t)dt = V(2) – V(1) \)

ここで\( V(t) \)は\( v(t) \)の不定積分です。

このように不定積分を大文字で表すことがよくあります。

微分の公式の三角関数の微分

\( \hspace{10pt} \displaystyle \frac{d}{dt} \cos t = -\sin t \)

から、\( \sin t \)の微分する前の関数である\( V(t) \)は、

\( \hspace{10pt} \displaystyle V(t) = -\cos t + c \)となります。

よって、

\( \hspace{10pt} \displaystyle \int_{1}^{2} v(t)dt =\left[ -\cos t + c \right]_{1}^{2} \)

\( \hspace{40pt} \displaystyle =\left\{ -\cos (2) + c \right\} – \left\{ -\cos (1) + c \right\} \)

\( \hspace{40pt} \displaystyle =-\cos (2) +\cos (1) \)

\( \hspace{40pt} \displaystyle =0.956[km] \)

となります。

ちなみに、最後の\( -\cos (2) +\cos (1) \)の計算はGoogle検索窓に左の式を入力することで計算結果がでます。

このように速度が時々刻々と変化する場合でも距離が計算できるのが積分のメリットです。