電場

目次（このページで分かること）

電場とは

電磁気学において、電荷から何らかのモノが放出されていると考えると、納得のいく現象がいくつかあります。

例えばクーロンの法則は距離の2乗に伴って力が減衰することを示しています。

これは電荷を中心とした半径$ R $の球を考え、その表面積が$4 \pi R^{2} $に伴って広がっていく事を踏まえると、電荷から放出されたものが表面積の広がりに応じて薄まっていくと考えると整合がとれます。

（「クーロンの法則」の「なぜ距離の2乗に反比例するのか」にも説明があります）

また、電荷が動くと、その影響は時間差をもって遠くの電荷に及びます。

まるで空間を何かが伝わっていくように。

これらのことから電荷があたかも物理的な実態を持つモノを放出しているようにも考えられます。

この動画はあくまでもイメージであり、そもそも本当に何かが放出されているかどうかも分かっていません。

しかし電磁気学では、このように電荷から何らかが放出されていると仮定し、それを電場と呼んでいます。

数式表現

クーロンの法則によれば、静止している電荷$ q $が、距離$ R $だけ離れた電荷$ Q $へ及ぼす力$ F $は次式になりました。

クーロンの法則（ベクトル表現）

$$ \displaystyle \mathbf{F} = \frac{1}{4 \pi \varepsilon_{0}} \frac{qQ}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $$

この式から力を受ける側の電荷$ Q $の要素を分けると、

$ \hspace{10pt} \displaystyle \mathbf{F} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\zeta^{2}} \hat{\boldsymbol{\zeta}} \cdot Q $

この$ Q $以外の部分を$ q$が作る電場として定義します。

電場

$$ \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $$

この数式にはいくつか注意点があります。

$ \boldsymbol{\zeta} = \mathbf{r}-\mathbf{r’} $

クーロンの法則のページで解説していますが、$ \boldsymbol{\zeta} $は次式になります。

$ \hspace{10pt} \boldsymbol{\zeta} = \mathbf{r}-\mathbf{r’} $

$ \mathbf{r} $は空間上の任意の点$ P $の位置ベクトル

クーロンの法則において、この$ \mathbf{r’} $ 、$ \mathbf{r} $はそれぞれ電荷$ q $、$ Q $の位置ベクトルでしたが、電場の計算では$ Q $は存在していません。

あくまで電場は電荷$q $がその周囲に作り出すものです。

よって、この電場の計算式では$ \mathbf{r} $を空間上の任意の点$ P $の位置ベクトルとします。

電場$ \mathbf{E} $は$\mathbf{r} $の関数：$ \mathbf{E} (\mathbf{r})$

電荷$ q $の位置ベクトルである$ \mathbf{r’} $や電荷量$ q $は所与の条件（あらかじめ与えられる条件）です。

よって、電場$ \mathbf{E} $は点$ P $の位置ベクトル$ \mathbf{r} $の関数$ \mathbf{E} (\mathbf{r}) $です。

空間上の任意の点のベクトルを計算する数式

数式にベクトル$ \hat{\boldsymbol{\zeta}} $が入っていますので、電場はベクトルです。

上のグラフのように電荷から点$ P $を向くベクトルになります。

つまり、先ほどの電場の式は、空間上の任意の点のベクトルを計算する数式になっています。

少し分かりにくいかもしれませんので、以下で電場をグラフ化してイメージを掴み、その後に例題で具体に電場を計算してみます。

電場の例

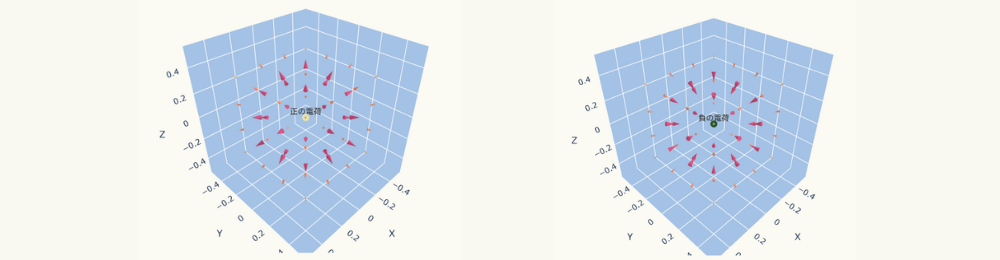
1個の正の電荷が作る電場

原点に置かれた1個の正の電荷が作る電場をグラフ化します。

グラフ作成プログラムの都合上、ベクトルをコーン状で表現しています。コーンの向きがベクトルの向き、コーンの大きさがベクトルの大きさです。（このグラフは回転できます）

電荷を中心として放射状に広がっていることが分かるかと思います。

また、電荷から遠ざかるとベクトルも小さくなっています。

電場の数式上、電荷からの距離の2乗に反比例して小さくなります。

このグラフでは一定の間隔で電場を計算していますが、より細かく計算することはできますし、もっと言えば空間上のあらゆる点で電場を計算できます。

ちなみに、このベクトルを流れに変換したものが先ほどの動画です。

1個の負の電荷

原点に置かれた負の電荷の場合は次のようになります。

正の電荷とは逆に電場のベクトルの向きは全て負の電荷に収束していく方向です。

電場の大きさは電荷からの距離の2乗に反比例して小さくなります。

先ほどと同様に、ベクトルと流れに変換すると。

時々出てくる長い線はプログラム上の「あや」です。消そうとしてもけせなかったもので・・・

例題

座標（1,0,1）の電荷$ q(-1[C]) $が点P（0,1,1）に作る電場を計算してください。

電場の計算式の不明な変数$ \zeta $、$ \hat{\boldsymbol{\zeta}} $を求めます。

電場

$$ \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $$

$ \hspace{10pt} \boldsymbol{\zeta} = \mathbf{r}-\mathbf{r’} $

$ \hspace{20pt} = (0,1,1)-(1,0,1) = (-1,1,0) $

ですので、

$ \hspace{10pt} \zeta = \sqrt{(-1)^{2} + 1^{2} + 0^{2}} = \sqrt{2} $

$ \hspace{10pt} \displaystyle \hat{\boldsymbol{\zeta}} = \frac{1}{\sqrt{2}}(-1,1,0)$

よって、

$ \hspace{10pt} \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $

$ \hspace{20pt} \displaystyle = \frac{1}{4 \pi \varepsilon_{0}} \frac{-1}{2\sqrt{2}} (-1, 1, 0) $

$ \hspace{20pt} \displaystyle = -\frac{1}{4 \pi \varepsilon_{0}} \frac{1}{2\sqrt{2}} (-1, 1, 0) $

となります。

グラフにすると、点$ P $から電荷方向を向くベクトルとなります。

このような計算を3次元空間内の一定間隔で行ってグラフ化したものが、「電場の例」のグラフです。