重ね合わせの原理(クーロンの法則)
ソース電荷(力を与える側の電荷)が複数ある場合、試験電荷(力を受ける側の電荷)が受ける力はどうなるでしょうか?

この場合、試験電荷が受ける力は個々のソース電荷が試験電荷に与える力を足したモノになります。
これをクーロンの法則における重ね合わせの原理と言います。
単純に力を足していけばいいということですね。
例えば、次のように\( q_{1} \)、\( q_{2} \)の二つのソース電荷がある場合、試験電荷\( Q \)に働く力\( F \)はどうなるでしょうか?

下の動画のように、\( q_{1} \)が\( Q \)に及ぼす力\( F_{1} \)と\( q_{2} \)が\( Q \)に及ぼす力\( F_{2} \)を足した力になります。
この数式
\( \hspace{10pt} \displaystyle F = F_{1} + F_{2} \)
$$ \displaystyle \mathbf{F} = \frac{1}{4 \pi \varepsilon_{0}} \frac{qQ}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $$
を使うと
\( \hspace{10pt} \displaystyle F =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}Q}{\zeta_{1}^{2}} \hat{\boldsymbol{\zeta}}_{1} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}Q}{\zeta_{2}^{2}} \hat{\boldsymbol{\zeta}}_{2} \)
となります。
一般化して、\( n \)個のソース電荷がある場合、この式は、
\( \hspace{10pt} \displaystyle F =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}Q}{\zeta_{1}^{2}} \hat{\boldsymbol{\zeta}}_{1} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}Q}{\zeta_{2}^{2}} \hat{\boldsymbol{\zeta}}_{2} + \cdots + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{n}Q}{\zeta_{n}^{2}} \hat{\boldsymbol{\zeta}}_{n}\)
となり、これを\( \sum \)を使ってまとめると、
$$ \displaystyle \mathbf{F} = \frac{Q}{4 \pi \varepsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\zeta_{i}^{2}} \hat{\boldsymbol{\zeta}}_{i} $$
これでソース電荷が複数ある場合の試験電荷が受ける力を求めることができます。
例題
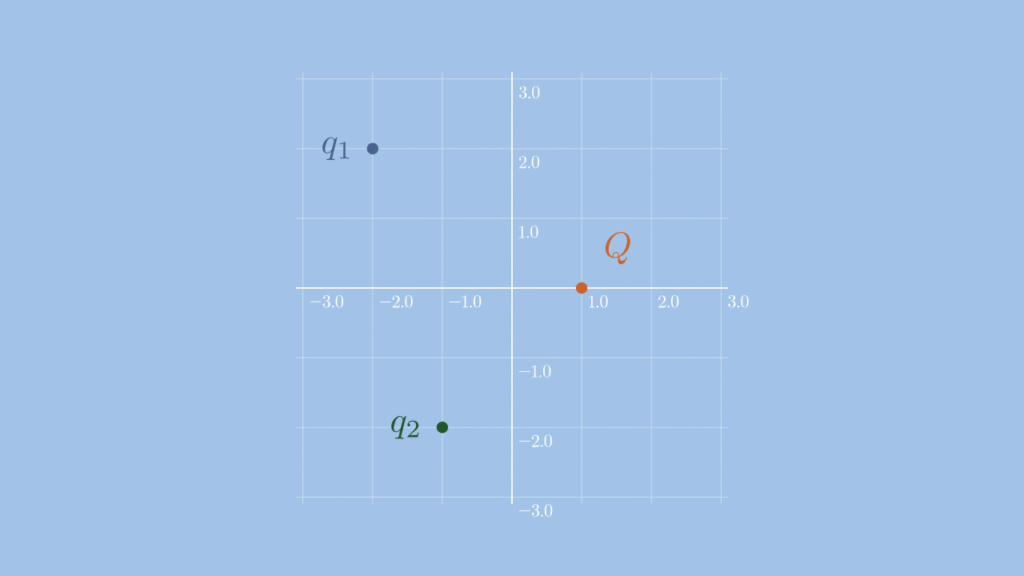
座標\( (-2,2) \)の\( q_{1} \)、座標\( (-1,-2) \)の\( q_{2} \)の二つのソース電荷が座標\( (1,0) \)に置かれた試験電荷\( Q \)に及ぼす力\( F \)を計算してください。
先ほどの例から、計算式は次式となります。
\( \hspace{10pt} \displaystyle F =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}Q}{\zeta_{1}^{2}} \hat{\boldsymbol{\zeta}}_{1} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}Q}{\zeta_{2}^{2}} \hat{\boldsymbol{\zeta}}_{2} \)
この中の不明な4つの変数\( \zeta_{1} \)、\( \hat{\boldsymbol{\zeta}}_{1} \)、\( \zeta_{2} \)、\( \hat{\boldsymbol{\zeta}}_{2} \)を求めます。
電荷\( q_{1} \)の位置ベクトルを\( \mathbf{r’}_{1} \)、電荷\( Q \)の位置ベクトルを\( \mathbf{r} \)とすると、ベクトル\( \boldsymbol{\zeta}_{1} \)は\( \mathbf{r’}_{1} \)と\( \mathbf{r} \)の差ですので、
\( \hspace{10pt} \boldsymbol{\zeta}_{1} = \mathbf{r}-\mathbf{r’}_{1} \)
下図のようになります。
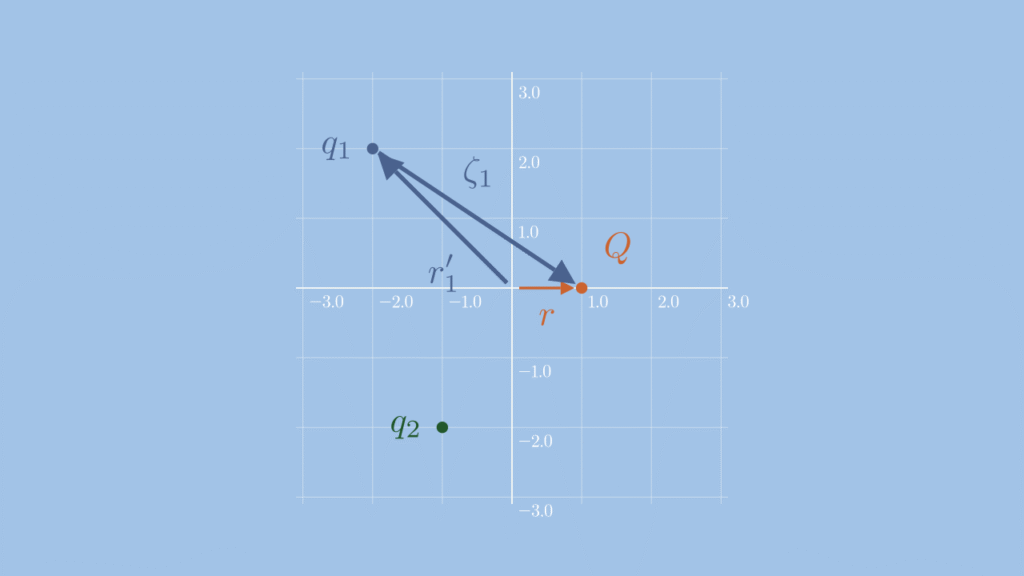
あとはこの\( \boldsymbol{\zeta}_{1} \)の大きさ\( \zeta_{1} \)と単位ベクトル\( \hat{\boldsymbol{\zeta}}_{1} \)を計算することになります。
\( \hspace{10pt} \displaystyle \zeta_{1} = |\mathbf{r}-\mathbf{r’}_{1}| \)
\( \hspace{15pt} \displaystyle = |(1 , 0)-(-2,2)| \)
\( \hspace{15pt} \displaystyle = |(3 , -2)| = \sqrt{3^{2}+ (-2)^{2}}\)
\( \hspace{15pt} \displaystyle = \sqrt{13}\)
\( \hspace{10pt} \displaystyle \hat{\boldsymbol{\zeta}}_{1} = \frac{(\mathbf{r}-\mathbf{r’}_{1})}{|\mathbf{r}-\mathbf{r’}_{1}|} \)
\( \hspace{15pt} \displaystyle = \frac{(3 , -2)}{\sqrt{13}}\)
同様に電荷\( q_{2} \)の位置ベクトルを\( \mathbf{r’}_{2} \)とすれば、
\( \hspace{10pt} \displaystyle \zeta_{2} = |\mathbf{r}-\mathbf{r’}_{2}| \)
\( \hspace{15pt} \displaystyle = |(1 , 0)-(-1,-2)| \)
\( \hspace{15pt} \displaystyle = |(2 , 2)| = \sqrt{2^{2}+ 2^{2}}\)
\( \hspace{15pt} \displaystyle = 2\sqrt{2}\)
\( \hspace{10pt} \displaystyle \hat{\boldsymbol{\zeta}}_{2} = \frac{(\mathbf{r}-\mathbf{r’}_{2})}{|\mathbf{r}-\mathbf{r’}_{2}|} \)
\( \hspace{15pt} \displaystyle = \frac{(2 , 2)}{2\sqrt{2}}\)
これを代入すれば、力\( F \)は
\( \hspace{10pt} \displaystyle F =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}Q}{(\sqrt{13})^{2}} \frac{(3 , -2)}{\sqrt{13}} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}Q}{(2\sqrt{2})^{2}} \frac{(2 , 2)}{2\sqrt{2}} \)
\( \hspace{15pt} \displaystyle =\frac{q_{1}Q}{4 \pi \varepsilon_{0}} \frac{(3 , -2)}{13\sqrt{13}} + \frac{q_{2}Q}{4 \pi \varepsilon_{0}} \frac{(2 , 2)}{16\sqrt{2}} \)
\( \hspace{15pt} \displaystyle =\frac{Q}{4 \pi \varepsilon_{0}} \left( \frac{3q_{1}}{13\sqrt{13}} + \frac{2q_{2}}{16\sqrt{2}}, \hspace{5pt} \frac{-2q_{1}}{13\sqrt{13}} + \frac{2q_{2}}{16\sqrt{2}} \right) \)
となります。
