k-means法(k平均法)とは
k-means法(k平均法)とは、与えられたデータをk個の中心点(平均値)からの近さを基準として、k個のクラスタ(集団)に分けるクラスタリングと呼ばれる手法の一つです。
次のグラフのようにクラスタリングされます。
(このグラフは回転できます)
例えばビジネスにおいては、顧客セグメンテーション(分類)、商品のカテゴリー分類、貸し倒れのリスク評価などに応用できます。
特徴(メリット・デメリット)
- 考え方がシンプル:直感的に分かりやすい手法
- 高速:k-means法は効率的で高速なアルゴリズムであり、大規模なデータセットに対しても適しています。
- 品質が初期化に依存:処理結果が初期クラスタ中心点の選択に依存するため、ランダムな初期化で不良なクラスタになる可能性があります。対応方法として、複数の初期化から結果を比較する方法があります。
- クラスタ数(k)の事前設定が難しい:適切なクラスタ数(k)の選択は難しい課題です。対応方法として、クラスタ数を選択する手法(エルボー法、シルエット分析)があります。
- クラスタ境界は直線(多角形):クラスタ間の境界が直線(多角形)になるため、円状など複雑な形状の分布には適していません。そういった分布にも対応可能なDBSCAN (Density-Based Spatial Clustering of Applications with Noise)といったクラスタリング手法があります。
このページでは回転できる3Dグラフや図を多用して、k-means法の手順、特徴、Pythonコード、理論について視覚的にわかりやすく解説します。
その後、サンプルデータ、Pythonコード付きで例題を解きます。
手順
手順を一通り示した後、具体例で実際にどのような感じになるのかを説明します。
標準化は次式のようにデータの値から平均値を引いたものを標準偏差で割ることです。
\( \hspace{10pt} \displaystyle 標準化:\hspace{10pt} \frac{データ値ー平均}{標準偏差} \)
(平均値や標準偏差について詳しく知りたい方は、「平均値、中央値、最頻値」「分散と標準偏差」をご覧ください。)
標準化した後のデータは平均値がゼロになり、標準偏差(データ分布の広がり(バラつき)の程度)が1になります。
標準化はデータのスケールが異なる場合に推奨されます。
例えば年収と年齢のデータセットの場合、年収の10円差と年齢の10歳差ではスケールが大きく異なります。
これにより、スケールの大きな方に引きずられ、クラスタリングが適切に機能しない可能性があります。
標準化を行うことで各変数の尺度の影響を均一にし、クラスタリング結果の品質を向上させることができます。
k-means法を適用する前に、データ点をいくつのクラスタに分けるかを決定します。
適切なクラスタ数を選ぶために、エルボー法、シルエット法などのクラスタ数選択の方法を使用できます。
与えられたデータ点からk個の中心点をランダムに選ぶ。
各データ点を、最も近いクラスタ中心点に割り当てます。
各クラスタの中心点を、そのクラスタに所属するデータポイントの平均位置(重心)に更新します。
平均値の計算式は次の通りです。
\( \hspace{10pt} \displaystyle 平均値= \frac{\boldsymbol{x}^{(1)} + \boldsymbol{x}^{(2)} + \boldsymbol{x}^{(3)} \cdots \boldsymbol{x}^{(n)}}{ n } \)
\( \hspace{20pt} \displaystyle = \frac{ \displaystyle \sum_{i=1}^{n}\boldsymbol{x}^{(i)} }{ n } \)
クラスタ中心が収束するまで、STEP4とSTEP5を繰り返します。
通常、収束条件は中心点の変化が小さくなるか、一定の回数繰り返した場合となります。
次のグラフのような身長と体重のデータ10個に対して、k-means法を使ってみます。
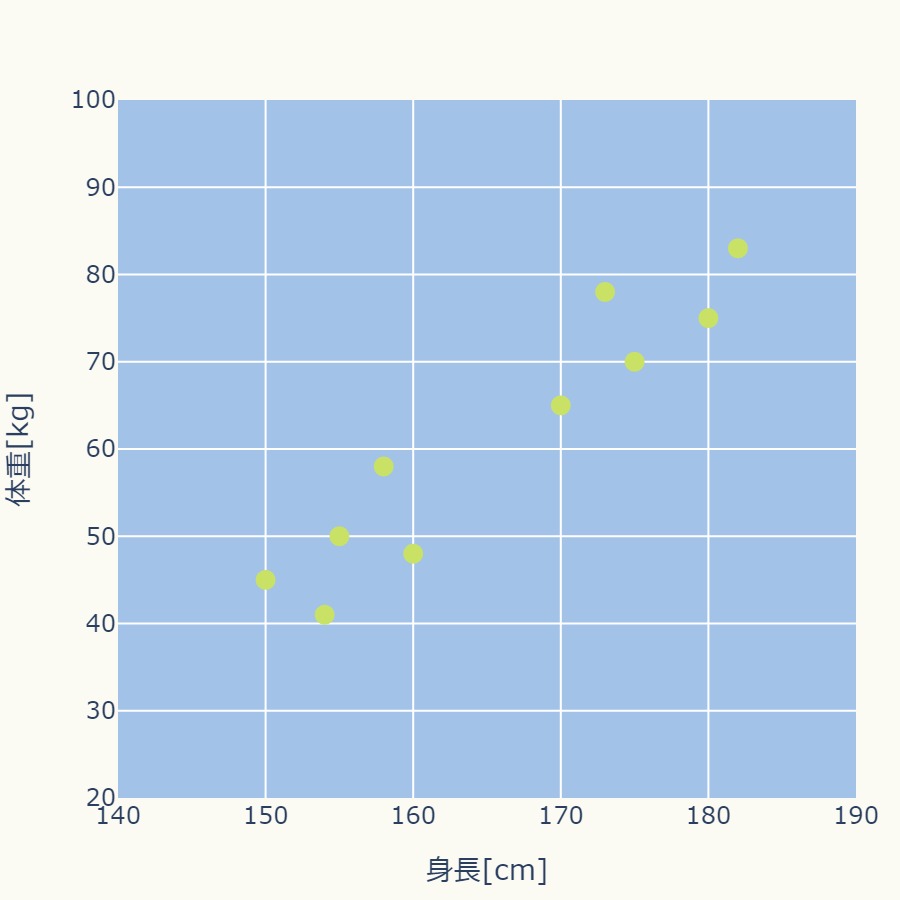
身長と体重ではスケールが異なります(身長は百数十のスケール、体重は数十のスケールです)ので、標準化処理をおこないます。
\( \hspace{10pt} \displaystyle 標準化:\hspace{10pt} \frac{データ値ー平均}{標準偏差} \)
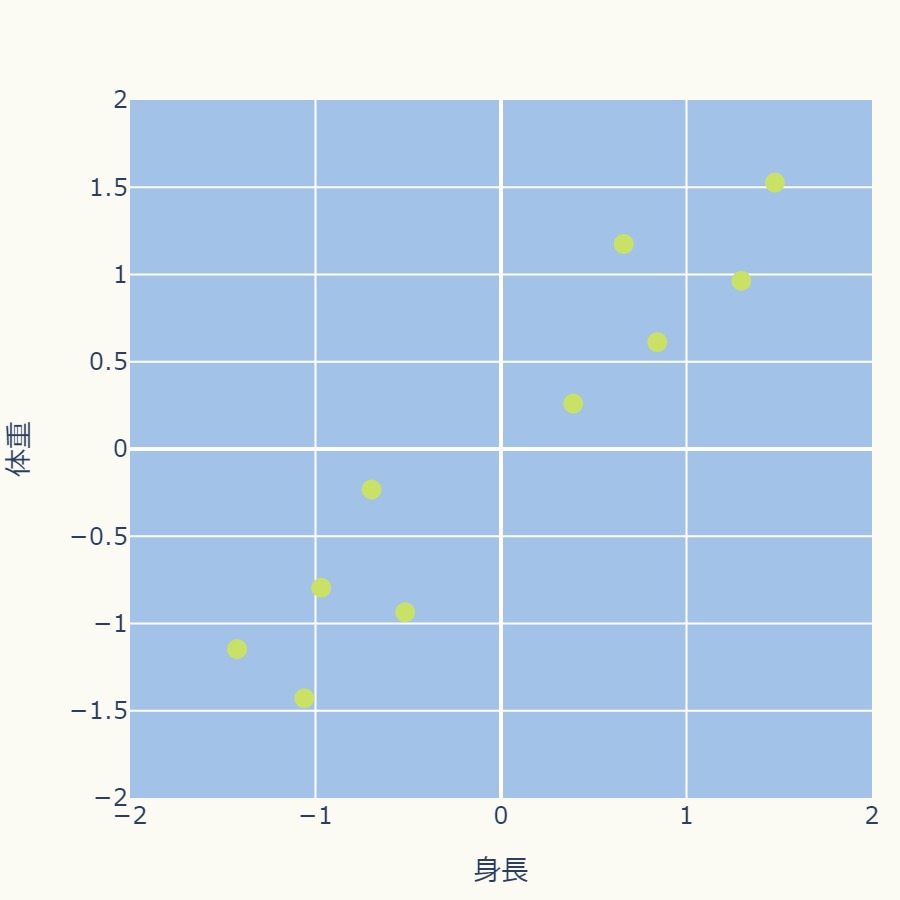
標準化処理によって、身長、体重ともにー2から+2の間ぐらいの分布になりました。
ここでは、k=2とします。
与えられたデータ点からk=2個の中心点をランダムに選ぶ。
次のグラフでは中心点を△で表現しています。
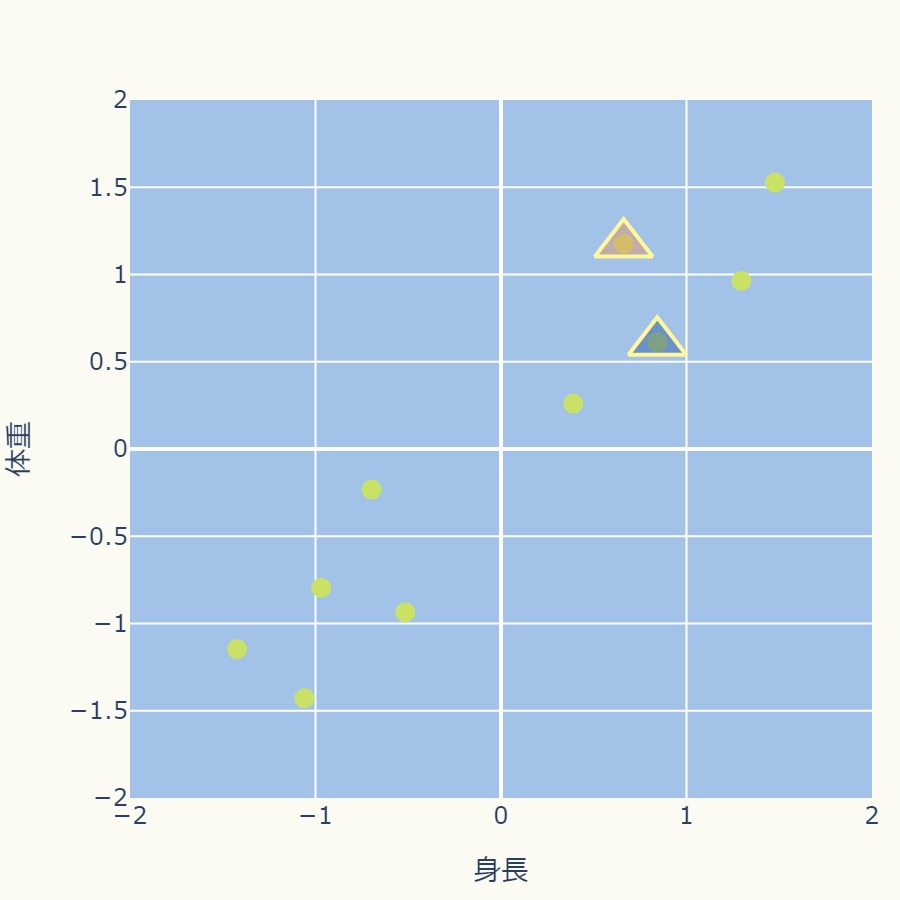
各データ点から2つの中心点までの距離を計算し、最も近いクラスタ中心に割り当てます。
下のグラフではオレンジと青で各クラスタを色分けしています。
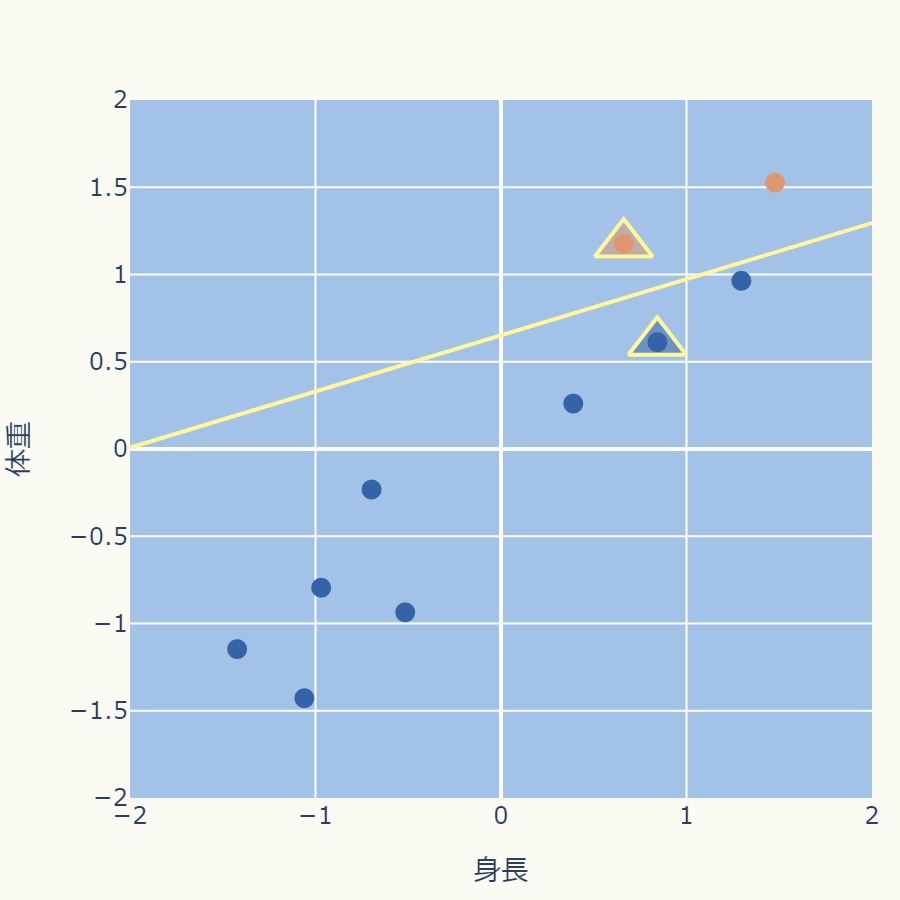
また、黄色の直線で示しているのは2つの中心点の中間を通る直線、つまり各中心点から等距離のラインです。
よって、この境界線でデータ点は異なるクラスタに割り当てられます。
各クラスタの中心を、そのクラスタに所属するデータ点の平均値(重心)に更新します。
オレンジのクラスタ(データ点2個)、青それぞれのクラスタ(データ点8個)ごとに平均値を計算して、更新します。
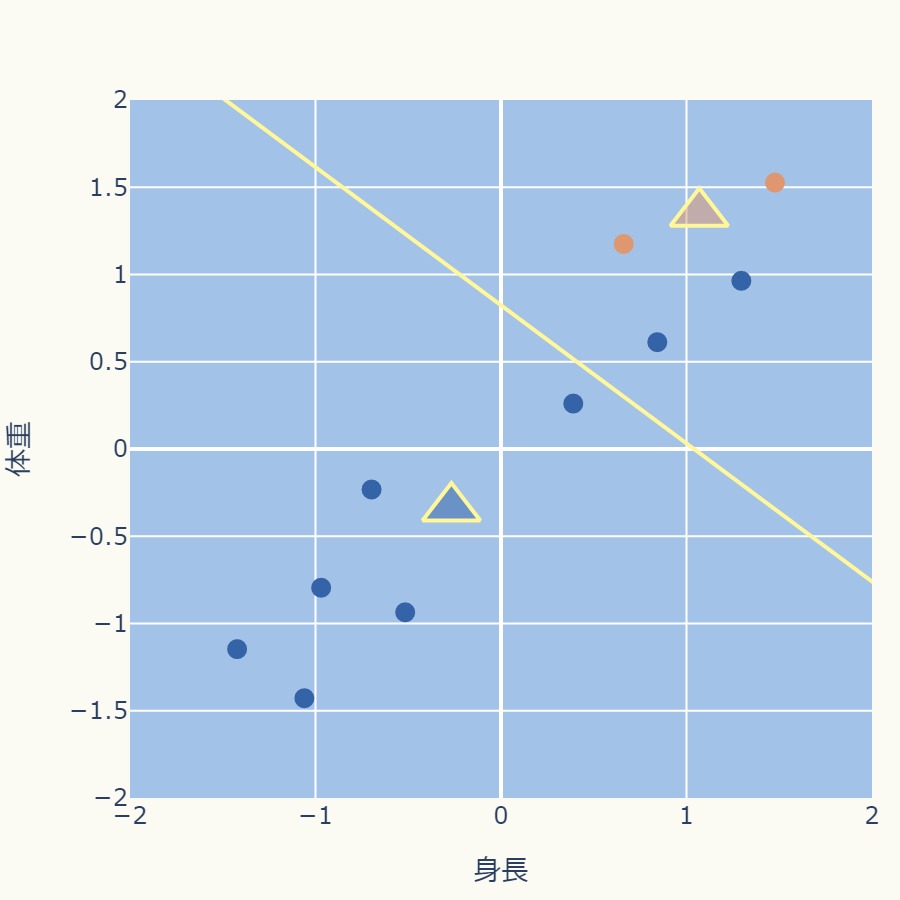
クラスタ中心が収束するまで、STEP4とSTEP5を繰り返します。
通常、収束条件は中心点の変化が小さくなるか、一定の回数繰り返した場合となります。
<STEP4:クラスタ割り当て>
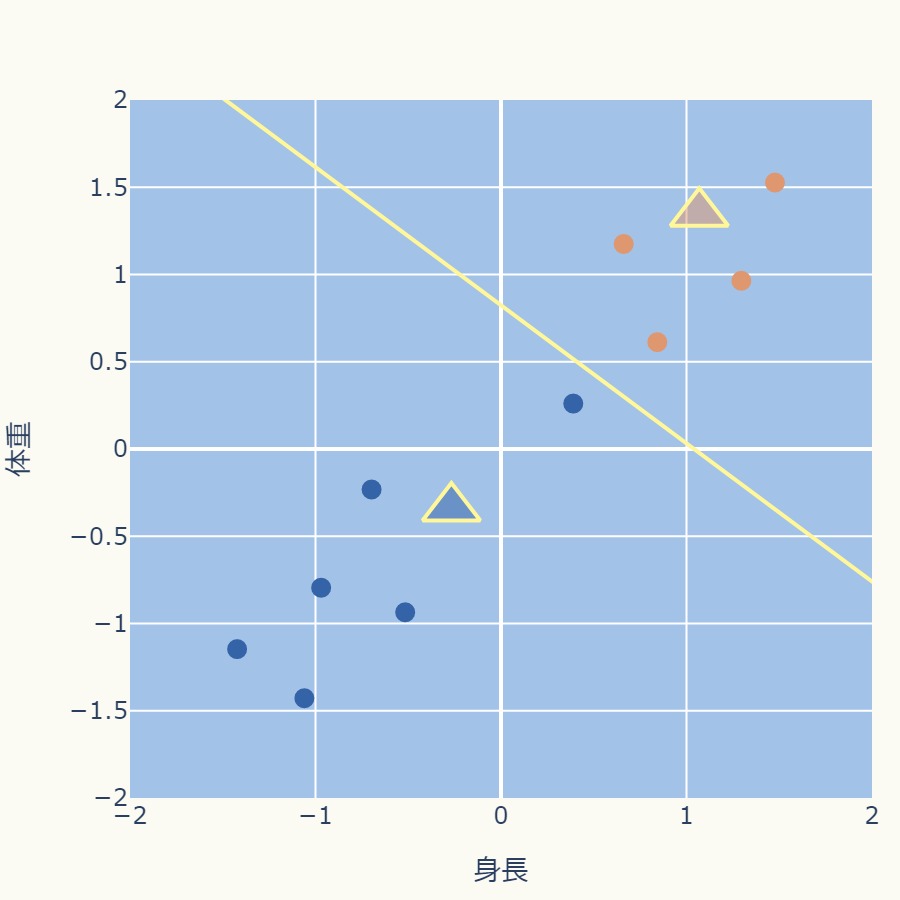
<STEP5:クラスタ中心点の更新>

<STEP4:クラスタ割り当て>
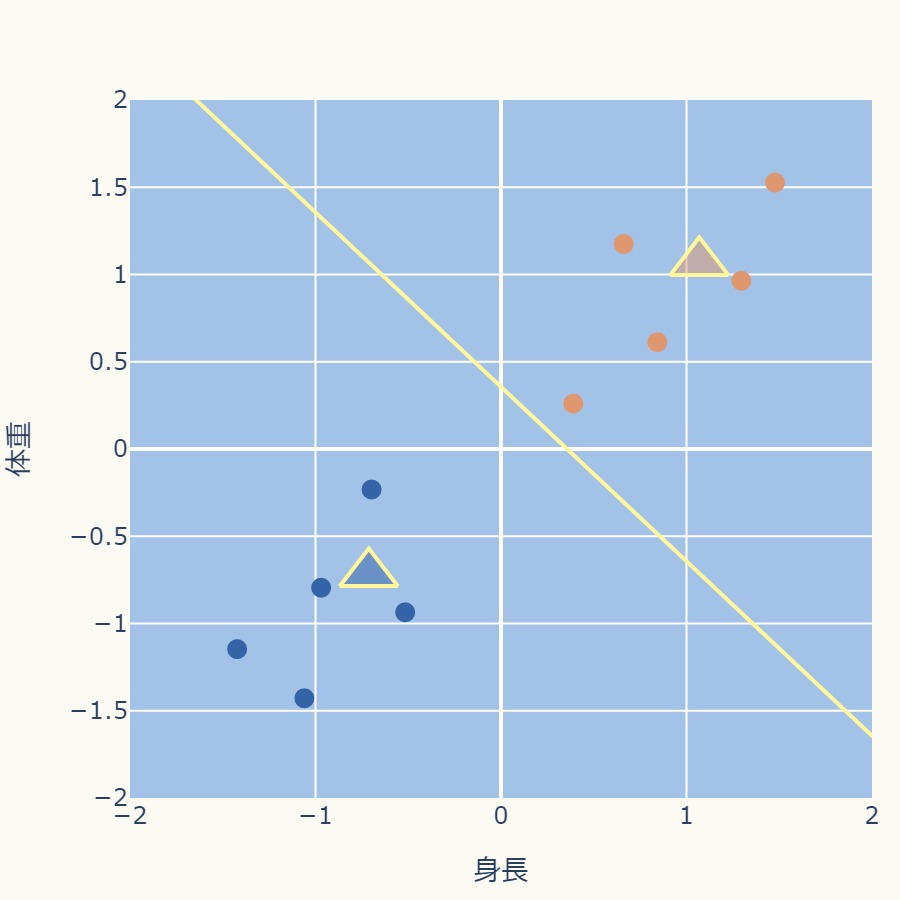
<STEP5:クラスタ中心点の更新>
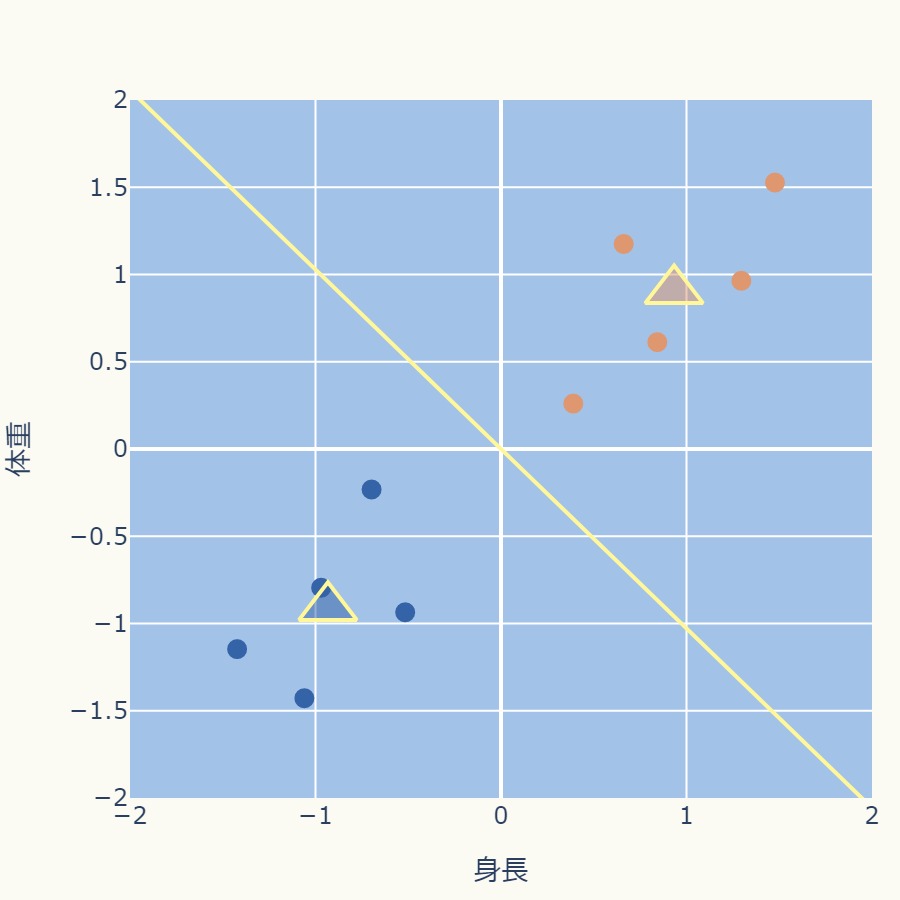
これ以降はクラスタの変動がなくなり、中心点の移動もなくなります。
これでクラスタリングは終了になります。
初期の中心点により不良のクラスタリングになる場合
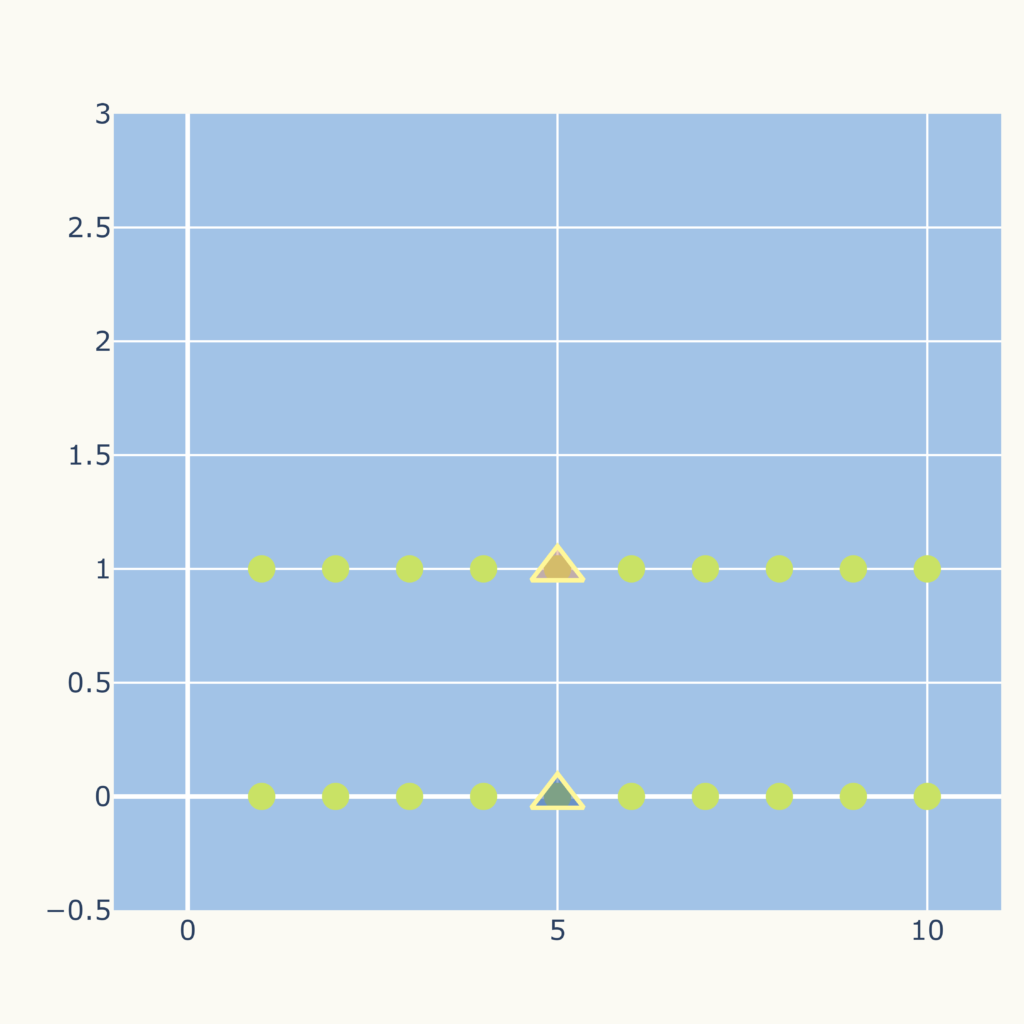
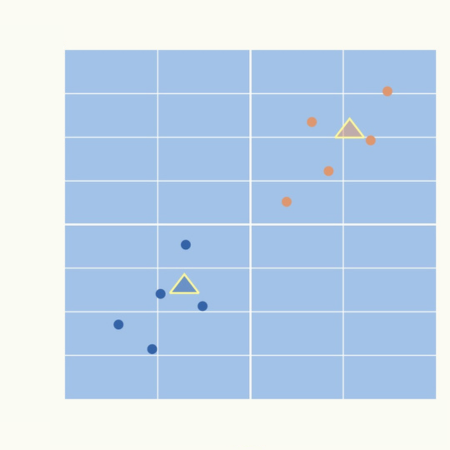
例えば下のようなデータ点(〇)、初期の中心点(△)であった場合、
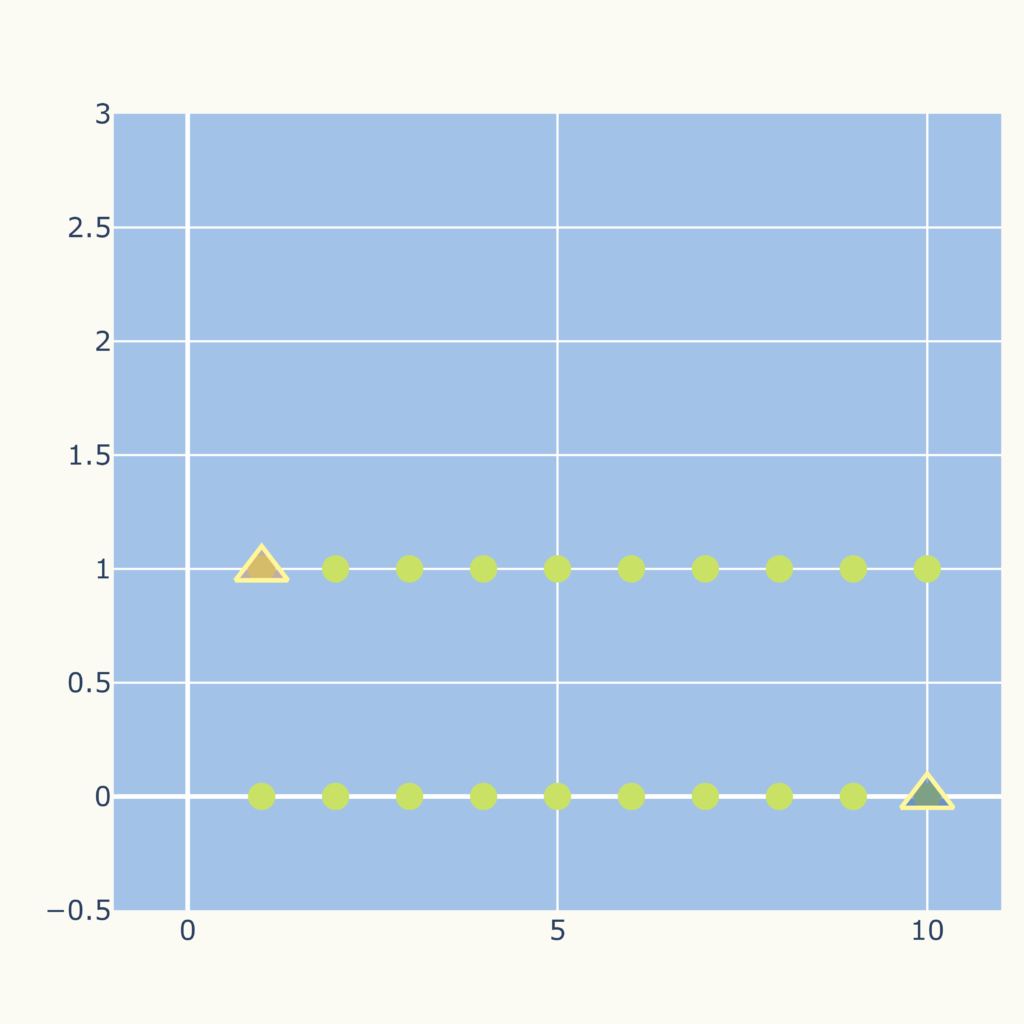
結果は次のグラフになります。
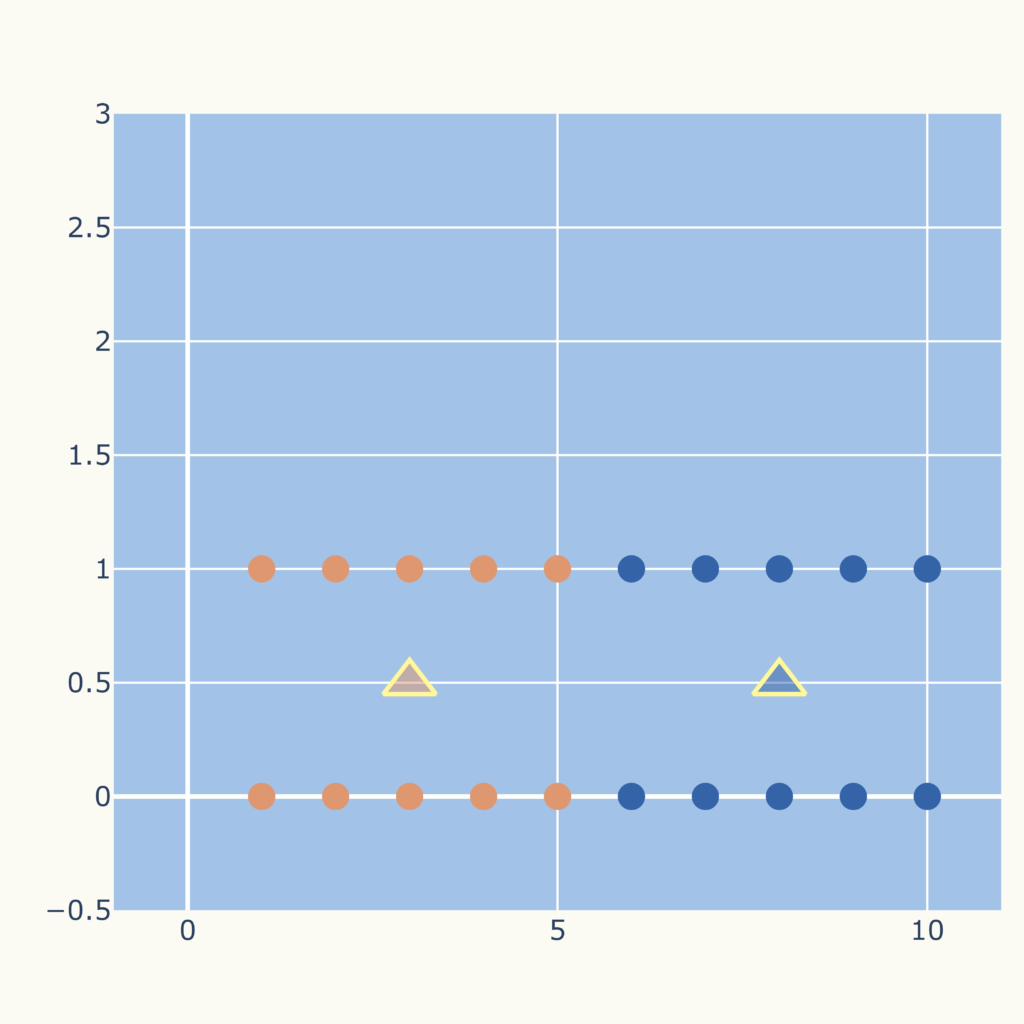
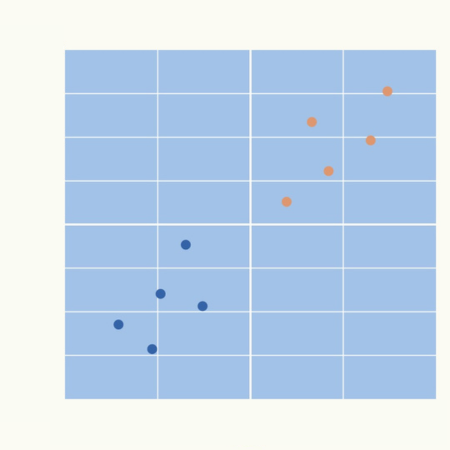
しかし、データの集団としてみるならば、次のグラフのようなクラスタリングが妥当と思われます。
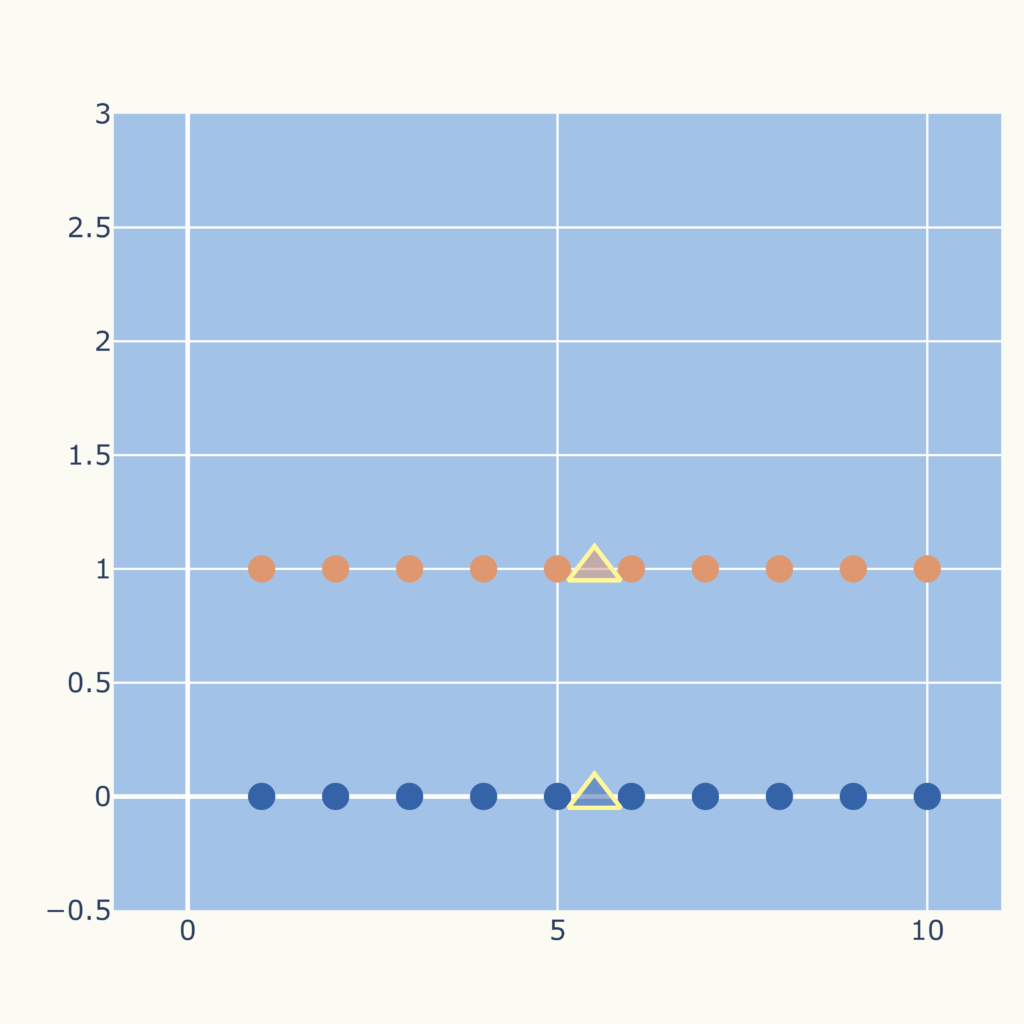
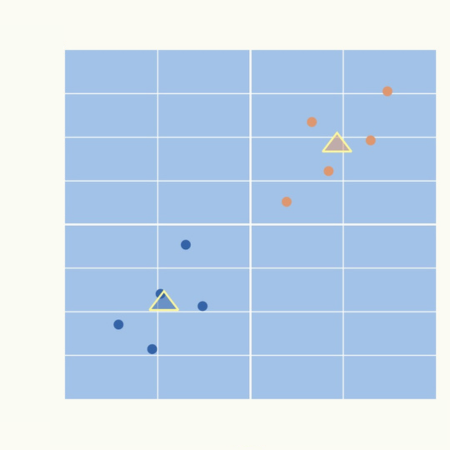
これは次の初期、中心点でk-means法を適用した結果です。
このように初期の中心点の選び方によって、結果が変わってきます。
このため、初期の中心点を変えて複数回k-means法を実施し、最も成績のよい結果を採用することで、不良な結果を回避できます。
評価基準は、「データ点から最も近いクラスタ中心点までの距離の二乗和」がより小さいこと、です。
具体の数式を見たい方は「理論の解説」の関数\( J \)をご覧ください。
クラスタの境界は直線(多角形)
クラスタ間の境界は直線(多角形)になります。
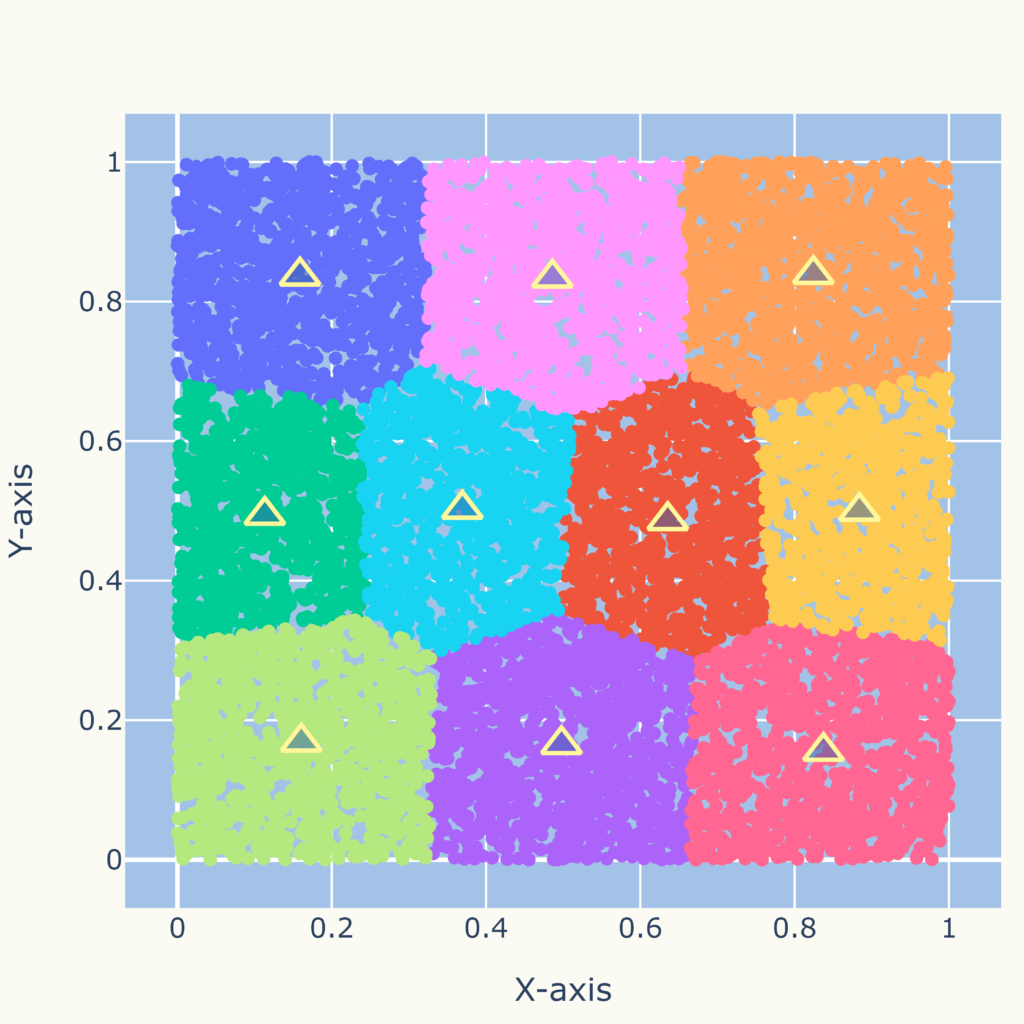
このため、次図のような複雑な分布に対しては適していません。
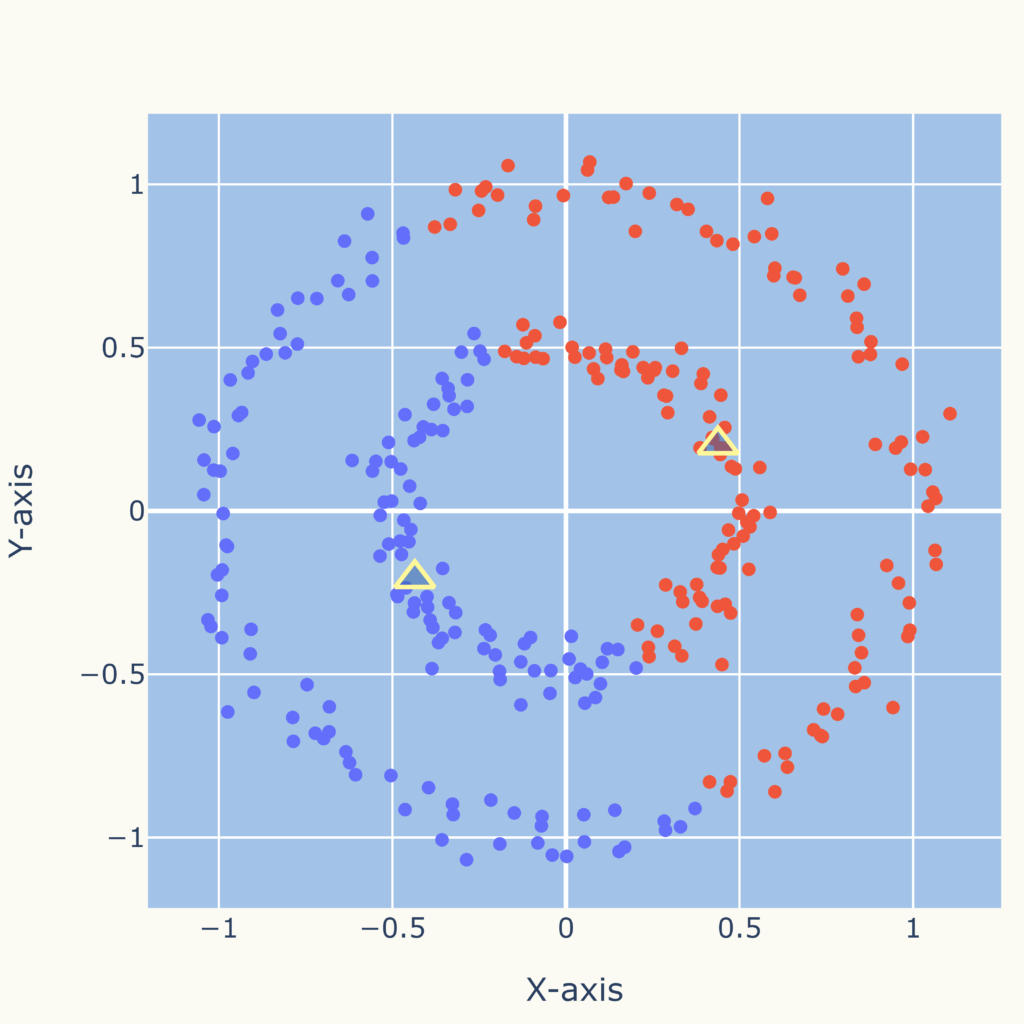
そういった分布にも対応可能なDBSCAN (Density-Based Spatial Clustering of Applications with Noise)といったクラスタリング手法があります。
Pythonコード
機械学習ライブラリを使用しない場合
コードは下記のとおりです。
コメントをご覧いただくと大体何をしているか分かると思いますが、上で説明した実施手順を行うことでk-means法を適用しています。
ただ、実際には次に紹介するscikit-learnライブラリを使用した方が簡単で、複数の初期化パターンを実行し、最も良い結果を選ぶこともできるので便利です。
# 機械学習ライブラリを使用しない場合
import numpy as np
import matplotlib.pyplot as plt
# ダミーデータ生成
data = np.array([[155, 50], [170, 65], [154, 41], [180, 75], [160, 48],
[175, 70], [150, 45], [182, 83], [158, 58], [173, 78]])
# データの標準化
mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
data = (data - mean) / std
# K-meansクラスタリングを手動で実行
k = 2 # クラスタ数
np.random.seed(0) # 再現性を保つためにシードを設定
# ランダムに初期クラスタ中心を選びます
initial_centers = data[np.random.choice(data.shape[0], k, replace=False)]
centers = initial_centers
# 最大の反復回数
max_iter = 100
for i in range(max_iter):
# 各データ点を最も近い中心点に割り当て
distances = np.sqrt(np.sum((data - centers[:, np.newaxis])**2, axis=2))
labels = np.argmin(distances, axis=0)
# 中心点を新たに計算
new_centers = np.array([data[labels == j].mean(axis=0) for j in range(k)])
# 収束判定
if np.all(centers == new_centers):
break
centers = new_centers
# クラスタ1とクラスタ2のデータを分離
cluster1 = data[labels == 0]
cluster2 = data[labels == 1]
# グラフにプロット
plt.figure(figsize=(8, 6))
plt.scatter(cluster1[:, 0], cluster1[:, 1], c='red', label='Cluster 1')
plt.scatter(cluster2[:, 0], cluster2[:, 1], c='blue', label='Cluster 2')
plt.scatter(centers[:, 0], centers[:, 1], c='black', marker='x', s=100, label='Cluster Centers')
plt.xlabel('Heihgt')
plt.ylabel('Weihgt')
plt.legend()
plt.title('K-means Clustering')
plt.show()
結果は次の通りです。
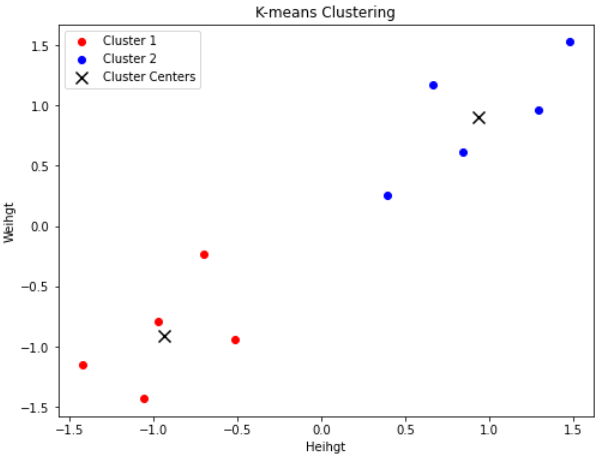
scikit-learnライブラリを使用した場合
コードは下記のとおりです。
# scikit-learnを使用した場合
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# データを作成
data = np.array([[155, 50], [170, 65], [154, 41], [180, 75], [160, 48], [175, 70], [150, 45], [182, 83], [158, 58], [173, 78]])
df = pd.DataFrame(data, columns=['Heihgt', 'Weight'])
# K-meansモデルを作成
kmeans = KMeans(n_clusters=2, init='random', n_init=10, max_iter=300, tol=1e-4, random_state=0)
# K-meansモデルをデータに適合
df['cluster'] = kmeans.fit_predict(df)
# クラスターごとにデータを可視化
plt.figure(figsize=(8, 6))
colors = ['r', 'g']
for i in range(2):
cluster_data = df[df['cluster'] == i]
plt.scatter(cluster_data['Heihgt'], cluster_data['Weight'], c=colors[i], label=f'Cluster {i+1}')
# クラスターの中心をプロット
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='k', marker='x', s=100, label='Cluster Centers')
plt.title('K-means Clustering')
plt.xlabel('Heihgt')
plt.ylabel('Weight')
plt.legend()
plt.show()
結果は次の通りです。
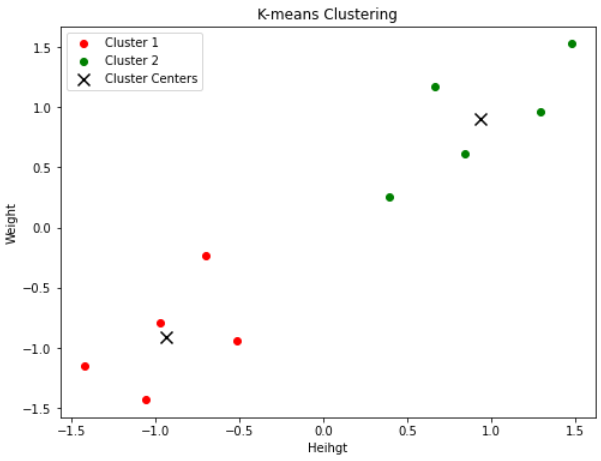
KMeansでモデルを作成し、fit_predict()でモデルをデータに適合させています。
fit_predict()の戻り値は各データ点が所属するクラスターを示す番号の配列です。
KMeansの主な引数、属性は次の通りです。
KMeansの主要な引数について詳しく説明します。
- n_clusters:
- クラスターの数を指定します。
- init:
- クラスターの初期化方法を指定します。
- デフォルトは”k-means++”で、効率的な初期化方法です。”random”はランダムな初期化です。
- n_init:
- 異なる初期化でk-meansアルゴリズムを実行する回数を指定します。
- 最良のクラスタリング結果を選びます。
- デフォルトは10です。
- max_iter:
- k-meansアルゴリズムの反復回数の上限を設定します。
- デフォルトは300です。
- tol:
- 収束判定の許容誤差を指定します。
- セントロイドの移動がこの誤差以下になるとアルゴリズムは収束とみなされます。
- デフォルトは1e-4(0.0001)です。
- random_state:
- 乱数生成のシードを指定します。
- 同じシードを使用すると、再現性のある結果が得られます。
K-meansモデルの主要な属性は以下の通りです:
1. cluster_centers_ :
- クラスターの中心点の座標を表す配列です。
2. labels_ :
- 各データポイントが所属するクラスターのラベルを表す配列です。データポイントごとにクラスターのラベルが割り当てられています。
3. inertia_ :
- データ点から最も近いクラスタ中心までの距離の二乗の合計を表す値です。この値が小さいほどクラスタリングが良好です。
4. n_iter_ :
- アルゴリズムが収束するまでの反復回数を示します。
これらの属性を使用することで、K-meansモデルの結果を分析し、クラスターの中心、クラスターへの所属データポイントなどの情報を取得できます。
理論の解説
\( n \)個のデータ(\( \boldsymbol{x}^{(1)} \cdots \boldsymbol{x}^{(i)} \cdots \boldsymbol{x}^{(n)} \))が与えられ、それらを\( k \)個の集団に分ける場合を考えます。
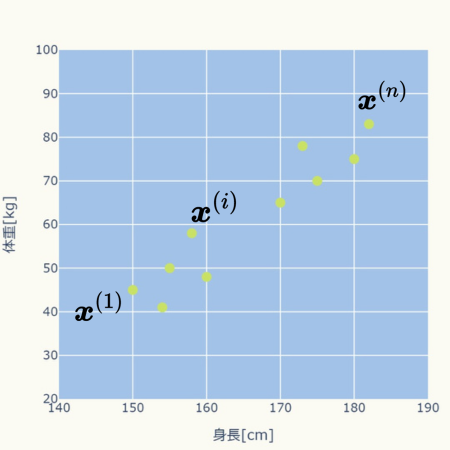
\( \boldsymbol{x}^{(i)} \)は一つのデータのセット([身長、体重]や[身長、体重、腹囲]のセット)であることに注意してください。
\( \hspace{10pt} \displaystyle \boldsymbol{x}^{(i)} = \left[ x^{(i)}_{1} \cdots x^{(i)}_{d} \right] \)
そして、このようなデータセットを\( d \)次元の位置ベクトル(原点を始点としたベクトル)と考えます。
例えば、データが[身長、体重]のセットであれば、\( \boldsymbol{x}^{(i)} \)は2次元の位置ベクトル、[身長、体重、腹囲]のセットであれば3次元の位置ベクトルと考えます。
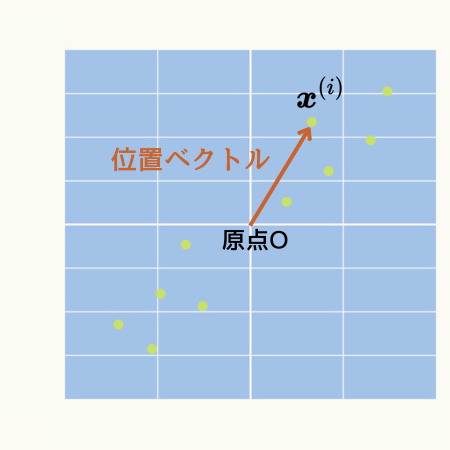
k-means法では座標上の2点間の距離を計算します。
もう少し下で分かりますが、位置ベクトルを使用することで、その計算式が簡潔に表現されます。
k-means法(k平均法)では、データ点から最も近いクラスタ中心点(\(\boldsymbol{\mu}^{(1)} \cdots \boldsymbol{\mu}^{(j)} \cdots \boldsymbol{\mu}^{(k)} \))までの距離の二乗和を最小にすることを目的とします。

この「データ点から最も近いクラスタ中心点までの距離の二乗和」を関数\( J \)で表したのが、次の関数です。
k-means法では、この関数の最小化が目的となります。
\( \hspace{10pt} \displaystyle J(w_{i,j},\boldsymbol{\mu}_{k}) = \sum^{n}_{i=1} \sum^{k}_{j=1} w_{i,j}\left| \boldsymbol{x}^{(i)} – \boldsymbol{\mu}^{(j)} \right|^{2}\)
ここで、\( w_{i,j} \)はデータ\( \boldsymbol{x}^{(i)} \)が所属する集団の割り振りを表すのもので、集団\( j \)に所属する場合は\( 1 \)、そうでない場合は\( 0 \)とします。
\( \hspace{10pt} \displaystyle w_{i,j} =\begin{cases}1 & (x_{i}が集団jに所属する) \\ 0 & (x_{i}が集団 j に所属しない) \end{cases} \)
また、\( \left| \boldsymbol{x}^{(i)} – \boldsymbol{\mu}^{(j)} \right| \)は位置ベクトルを使って中心点とデータ点の距離を計算しています。
(詳しく知りたい方は「位置ベクトルを使用した点間距離の計算」をご覧ください)
\( \boldsymbol{x}^{(i)} \)は与えれれたデータ(定数)ですので、関数\( J \)を最小化する\( w_{i,j} \)と\( \boldsymbol{\mu}^{(k)} \)を見つけることが目的となります。
これを次の2つのステップに分けて行います。
- \( \boldsymbol{\mu}^{(j)} \)を固定して、関数\( J \)を最小化する\( w_{i,j} \)を見つける
- \( w_{i,j} \)を固定して、関数\( J \)を最小化する\( \boldsymbol{\mu}^{(j)} \)を見つける
クラスタの中心点\( \boldsymbol{\mu}^{(j)} \)は固定です。
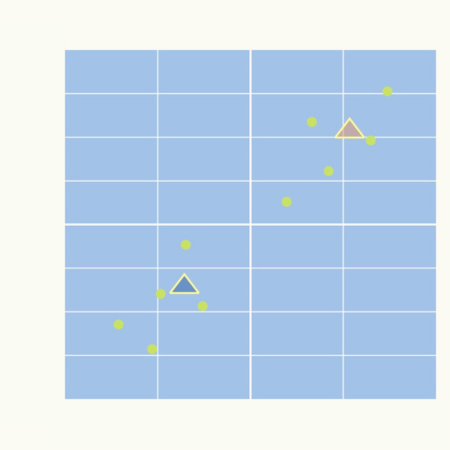
これはデータ\( \boldsymbol{x}^{(i)} \)を\( \left| \boldsymbol{x}^{(i)} – \boldsymbol{\mu}^{(j)} \right|^{2} \)が最も小さくなるような集団\(j\)に割り振ることになります。
言い換えると、データ\( \boldsymbol{x}^{(i)} \)を最も近い中心点\( \boldsymbol{\mu}^{(j)} \)のクラスタに割り振ることになります。
各集団への割り振り\( w_{i,j} \)は固定です。
例えば、集団\( j \)の場合を考えてみましょう。
\( \hspace{10pt} \displaystyle J(\boldsymbol{\mu}_{j}) = \sum^{n}_{i=1} w_{i,j}\left| \boldsymbol{x}^{(i)} – \boldsymbol{\mu}^{(j)} \right|^{2}\)
\( \hspace{20pt} \displaystyle = \sum^{n}_{i=1} \left\{ w_{i,j}\left( x^{(i)}_{1} – \mu^{(j)}_{1} \right)^{2} + w_{i,j}\left( x^{(i)}_{2} – \mu^{(j)}_{2} \right)^{2} + \cdots + w_{i,j}\left( x^{(i)}_{d} – \mu^{(j)}_{d} \right)^{2} \right\} \)
この\( J(\boldsymbol{\mu}^{(j)}) \)はスカラーの多変数関数であり、例えば2変数関数の場合(次元数\( d=2 \)の場合)は次のグラフのような下に凸の形になります。
このグラフは回転できます。
この場合、勾配ベクトルがゼロになるところで最小値になります。
(グラフ下の平面にコーン状で勾配ベクトルを表しています)
\( \hspace{10pt} \displaystyle 勾配ベクトル = \nabla J = \frac{\partial J}{\partial \mu^{(j)}_{1}} \boldsymbol{e}_{1} + \frac{\partial J}{\partial \mu^{(j)}_{2}} \boldsymbol{e}_{2} + \cdots + \frac{\partial J}{\partial \mu^{(j)}_{d}} \boldsymbol{e}_{d} = 0\)
\( \hspace{20pt} \displaystyle = \left\{ 2 \sum^{n}_{i=1} w_{i,j}\left( x^{(i)}_{1} – \mu^{(j)}_{1} \right) \right\} \boldsymbol{e}_{1} \)
\( \hspace{30pt} \displaystyle + \left\{ 2 \sum^{n}_{i=1} w_{i,j}\left( x^{(i)}_{2} – \mu^{(j)}_{2} \right) \right\} \boldsymbol{e}_{2} \)
\( \hspace{30pt} \displaystyle + \cdots \)
\( \hspace{30pt} \displaystyle + \left\{ 2 \sum^{n}_{i=1} w_{i,j}\left( x^{(i)}_{d} – \mu^{(j)}_{d} \right) \right\} \boldsymbol{e}_{d} \)
同じような数式が出てきていますので、\( \boldsymbol{e}_{1} \)の係数に注目して計算すると、
\( \hspace{10pt} \displaystyle \sum^{n}_{i=1} w_{i,j}\left( x^{(i)}_{1} – \mu^{(j)}_{1} \right) = 0 \)
から、
\( \hspace{10pt} \displaystyle \mu^{(j)}_{1} = \frac{\displaystyle \sum^{n}_{i=1} w_{i,j} x^{(i)}_{1}}{\displaystyle \sum^{n}_{i=1} w_{i,j}} \)
この式の分子は、\( w_{i,j} \)によって集団\( j \)に所属するデータのみ選ばれるため「集団jに所属するデータ値の総和」になります。
また分母は、集団\( j \)に所属するデータの数だけ\( w_{i,j} = 1)になるので、「集団jに所属するデータ数」となります。
\( \hspace{10pt} \displaystyle \mu^{(j)}_{1} = \frac{集団jに所属するデータ値の総和}{ 集団jに所属するデータ数 } \)
となり、これは集団\( j \)に所属するデータの平均値の計算式です。
他の次元についても同様の数式になり、
\( \hspace{10pt} \displaystyle \boldsymbol{\mu}^{(j)} = \left[ \frac{\displaystyle \sum^{n}_{i=1} w_{i,j} x^{(i)}_{1}}{\displaystyle \sum^{n}_{i=1} w_{i,j}} , \frac{\displaystyle \sum^{n}_{i=1} w_{i,j} x^{(i)}_{2}}{\displaystyle \sum^{n}_{i=1} w_{i,j}} \cdots \frac{\displaystyle \sum^{n}_{i=1} w_{i,j} x^{(i)}_{k}}{\displaystyle \sum^{n}_{i=1} w_{i,j}} \right] \)
結局、\( \boldsymbol{\mu}^{(j)} \)は集団\( j \)に所属するデータの平均値になります。
これがk-means法(k平均法)の名前の由来です。
なお、平均値はデータ分布の重心の位置とも解釈できるため、書籍やサイトによっては、中心点を重心と呼ぶこともあります。
(平均値が重心の位置になる理由を知りたい方は「平均値の物理的な解釈 ~ データ分布の重心位置 ~」をご覧ください)
k-means法(k平均法)では①と②の最小値を見つけるステップを繰り返すことにより関数\( J \)(「中心点からの距離の二乗和」)を減少させていきます。
こうすることで、与えられたデータを\( k \)個の中心点(平均値)に集団に振り分けます。
例題
顧客セグメンテーション
あるWebサイトの顧客の「年齢」、サイトの「滞在時間」、「平均購買額」のデータは次のグラフのようになりました。
k-means法を使用し、このデータを3つにクラスタリングしてください。
csv形式のデータを次のボタンからダウンロードできます。
(このデータは例題用に作成した疑似データです)
例えば次のようなコードになります。
コードは長いですが、ほとんどはグラフ化のコードです。
なお、グラフ化はplotlyライブラリを使用しています。
インストールされていない場合は、pipなどでインストールできます。
pip install plotly(詳しくインストール方法を知りたい方ははこちら)
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import plotly.graph_objs as go
# 生成したデータを読み込み
# (同じフォルダを前提としています)
data = pd.read_csv('./KMeanExampleCustomerSegmentation.csv', encoding = "shift-jis")
# データを標準化
scaler = StandardScaler()
X_std = scaler.fit_transform(data)
# k-meansクラスタリングを実行
k = 3 # クラスタ数
kmeans = KMeans(n_clusters=k, init='random', random_state=0)
data['クラスタ'] = kmeans.fit_predict(X_std)
data['クラスタ'] = data['クラスタ'].astype(str) # クラスタラベルを文字列に変換
# k-meansの中心点を取得
centers = scaler.inverse_transform(kmeans.cluster_centers_)
# 3Dプロット用のトレースを作成
traces = []
for cluster in range(k):
cluster_data = data[data['クラスタ'] == str(cluster)]
trace = go.Scatter3d(
x=cluster_data['平均購買額'],
y=cluster_data['滞在時間'],
z=cluster_data['年齢'],
mode='markers',
name=f'クラスタ {cluster+1}',
marker=dict(
size=3,
opacity=0.8
)
)
traces.append(trace)
# 中心点のトレースを追加
trace_centers = go.Scatter3d(
x=centers[:, 0],
y=centers[:, 1],
z=centers[:, 2],
mode='markers',
name='中心点',
marker=dict(
size=10,
opacity=1.0,
symbol='cross'
)
)
traces.append(trace_centers)
layout = go.Layout(
margin=dict(l=0, r=0, b=0, t=0),
scene=dict(
xaxis=dict(title='平均購買額'),
yaxis=dict(title='滞在時間'),
zaxis=dict(title='年齢'),
aspectratio=dict(x=1, y=1, z=1)
)
)
fig = go.Figure(data=traces, layout=layout)
fig.show()
配色とかの見た目は異なりますが、大体次のようなグラフになるかと思います。