順列、組合せ

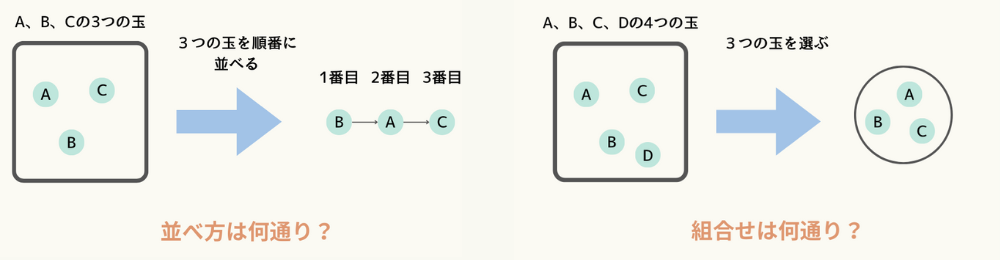
順列とは

順列とは複数のモノを順番をつけて並べること。また、その並べ方の総数のことです。

例１：　３個の球から３個並べる

例えば、A、B、Cと書かれた球が3個あったとします。

この３個の球を順番をつけて並べる場合、その並べ方は何通りになるでしょうか。

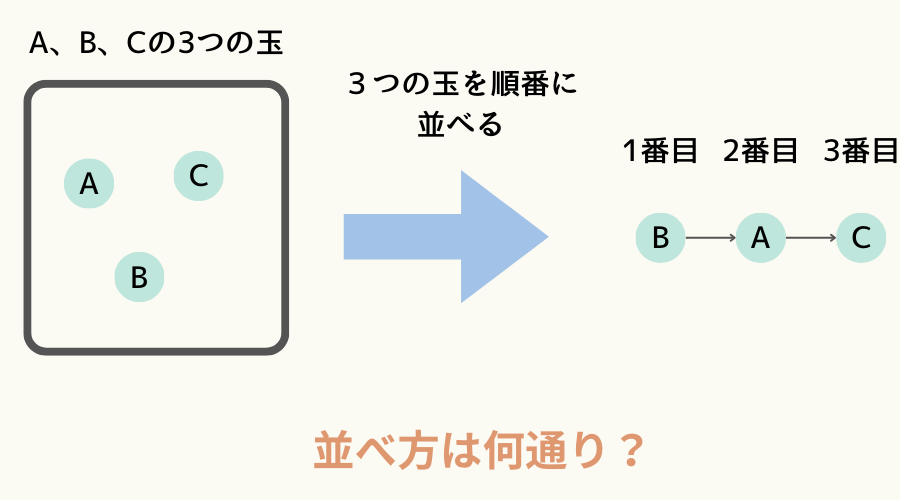
調べるために、次のように全ての並べ方を書いた樹形図を書いてみます。

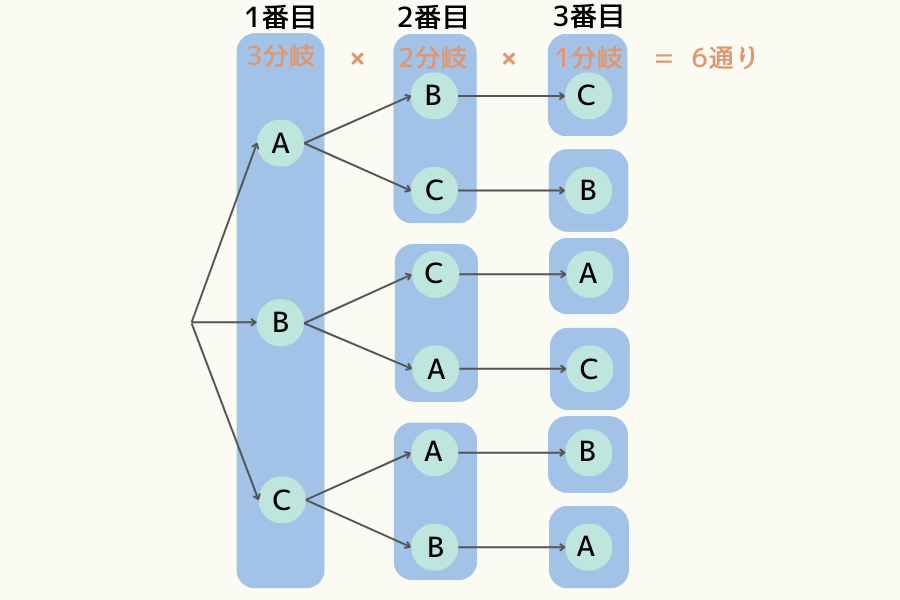
１番目にはA、B、Cいずれも選ぶことができるので、A、B、Cが入ります。

さらに、１番目がAの場合２番目にはB、Cいずれも選ぶことができるので、B、Cが入ります。

さらに、１番目がAで２番目がBの場合、３番目は残りのCだけ選ぶことができるので、Cが入ります。

このようにして作ったモノが上の樹形図です。

この図を見ると分かるように１番目で３分岐、２番目で２分岐、３番目で１分岐（分岐なし）なので、全ての組合せの数としては\( 3 \cdot 2 \cdot 1 = 6 \)となります。

例２：　４個の玉から４個並べる

今度は、A、B、C、Dと書かれた球が４個あったとして、４個の球を順番をつけて並べる場合、その並べ方は何通りになるでしょうか。

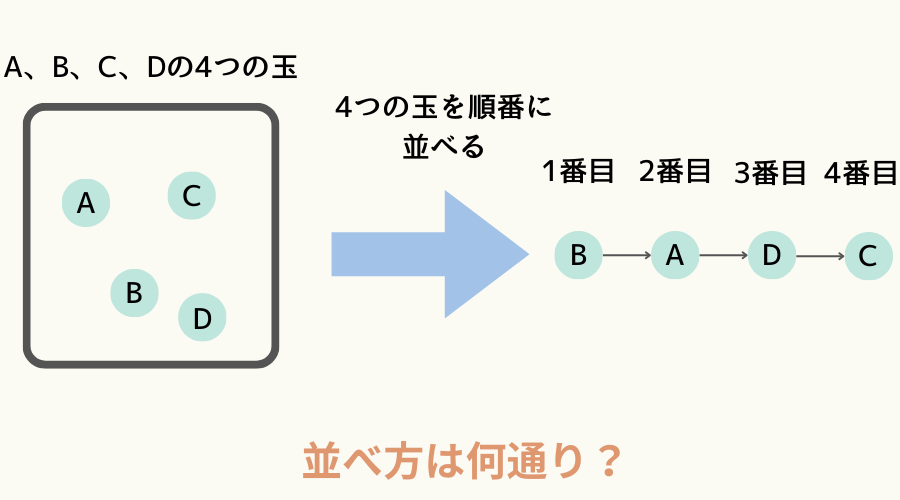
同様に樹形図を書くと次になります。

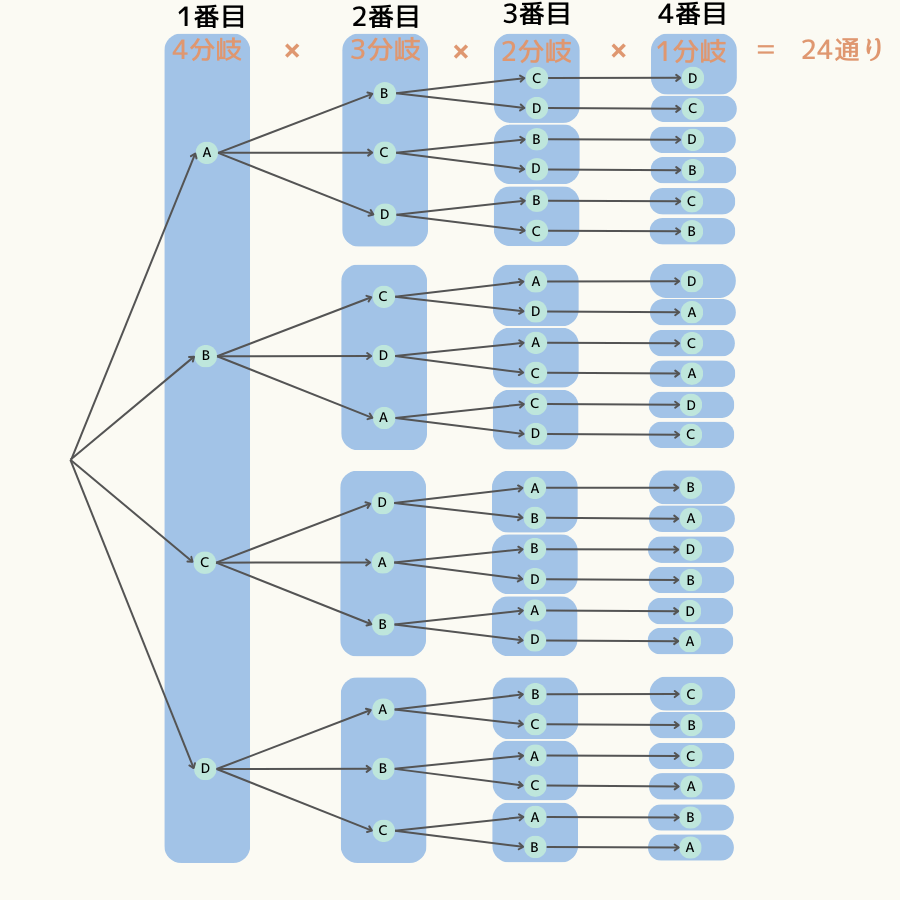
このことから、並べ方の総数は\( 4 \cdot 3 \cdot 2 \cdot 1 = 24 \)通りです。

例３：４個の玉から２個並べる　

同じようにA、B、C、Dと書かれた球が４個あったとして、今度は２個の球を順番をつけて並べる場合、その並べ方は何通りになるでしょうか。

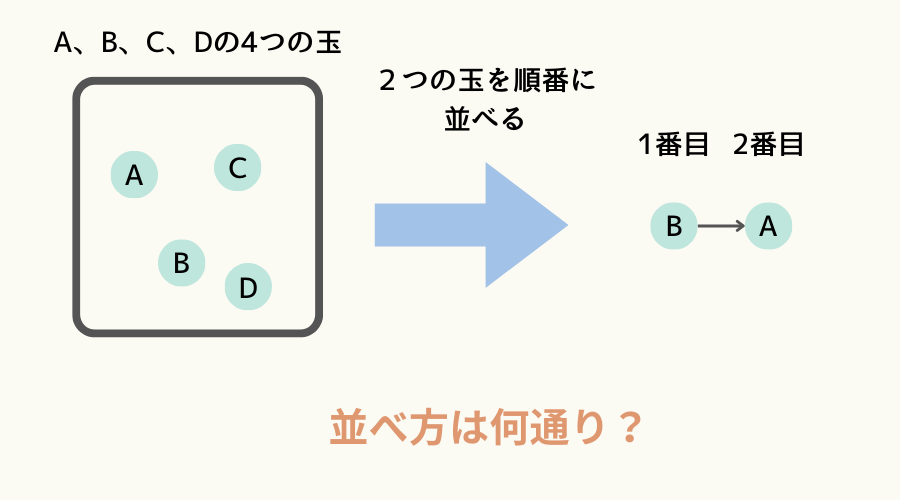
この場合、樹形図は例２の４個並べる場合の樹形図の２番目までで終わりになります。

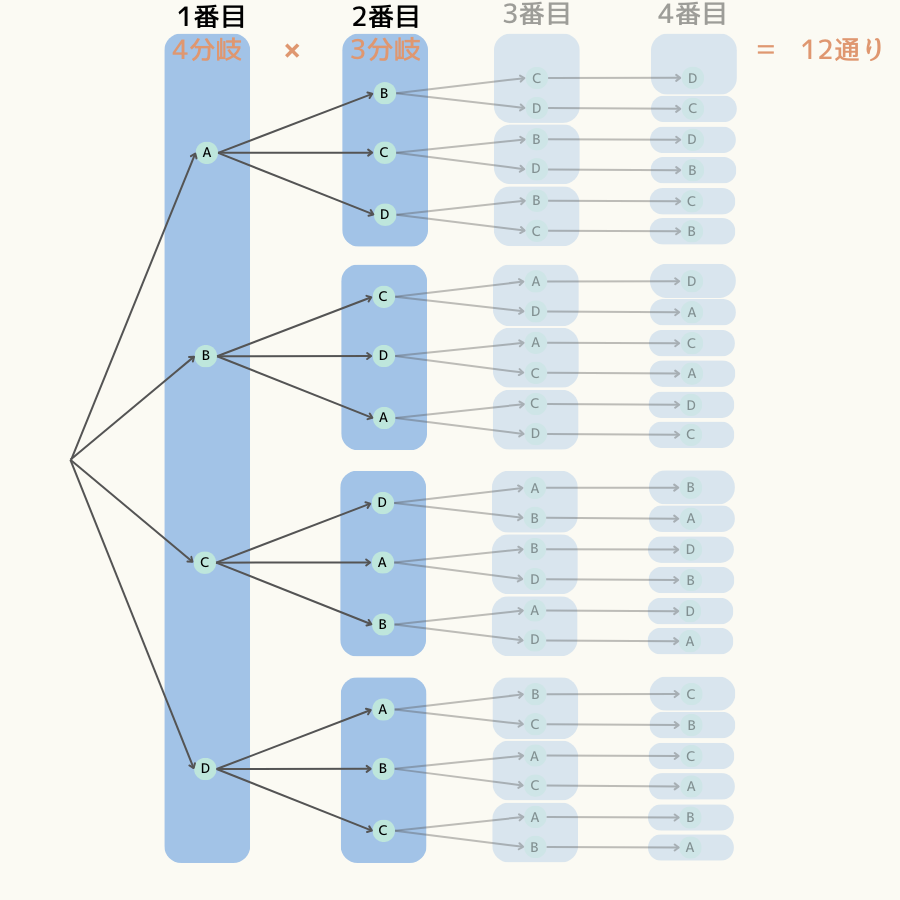
このことから、並べ方の総数は\( 4 \cdot 3 = 12 \)通りです。

同様に例えば４個の中の３個を順番に並べる場合は樹形図は三番目までになるので、並べ方の総数は\( 4 \cdot 3 \cdot 2 = 24 \)通りになります。

以上をまとめると次になります。

• ３個の中の３個を順番に並べる場合⇒ \( 3 \times 2 \times 1 \)通り
• ４個の中の４個を順番に並べる場合⇒ \( 4 \times 3 \times 2 \times 1 \)通り
• ４個の中の２個を順番に並べる場合⇒ \( 4 \times 3 \)通り
• ４個の中の３個を順番に並べる場合⇒ \( 4 \times 3 \times 2 \)通り

だいたい規則性が見えてきたのではないでしょうか。

４個の中から４個の場合は\( 4 \times 3 \times 2 \times 1 \)の４つの掛け算。

４個の中から３個の場合は\( 4 \times 3 \times 2 \)の３つの掛け算。

４個の中から２個の場合は\( 4 \times 3 \)の２つの掛け算。

一般化した書き方をすると次のようになります。

\( n \)個の中の\( r \)個（ただし、\( r \text{≦} n \) ）を順番に並べる場合、\( n \) から\( 1 \)までの整数のうち数の大きい方から\( r \)個の積。

ちなみに、上記の内、\( r = n \)の場合（全てを並べる場合）は\( n \) から\( 1 \)までの全ての整数（\( n \) 個）の積になります。

これを数式で表すと次の「順列の公式」になります。

順列の公式

（スマホでご覧の方へ、画面からはみ出してしまう数式はスクロールできます。）

\( n \)個の中から\( r \)個を並べる順列は次式となります。
\( \hspace{10pt} \displaystyle {}_n \mathrm{P}_r = \underbrace{ n(n-1)(n-2) \cdots (n-r+1) }_{r個の積} \)
\( \hspace{25pt} \displaystyle = \frac{n!}{(n-r)!} \)

公式の下段の式は上段の式を階乗の記号を使って簡潔に表現したものです。

例えば３個の中の３個を順番に並べる場合は次になります。

\( \hspace{10pt} \displaystyle {}_3 \mathrm{P}_3 = 3(3-1)(3-3+1) = 3 \cdot 2 \cdot 1 \)

\( \hspace{25pt} \displaystyle = \frac{3!}{(3-3)!} = \frac{3!}{(0)!} = \frac{ 3 \cdot 2 \cdot 1}{1} = 3 \cdot 2 \cdot 1 \)

公式の上段の計算式でも下段の計算式でも同じになります。

また、例えば４個の中の２個を順番に並べる場合は次になります。

\( \hspace{10pt} \displaystyle {}_4 \mathrm{P}_2 = 4(4-2+1) = 4 \cdot 3 \)

\( \hspace{25pt} \displaystyle = \frac{4!}{(4-2)!} = \frac{4!}{2!} = \frac{ 4 \cdot 3 \cdot 2 \cdot 1 }{ 2 \cdot 1 } = 4 \cdot 3 \)

同様に公式の上段の計算式も下段の計算式も結果は同じです。

Pythonによる順列の計算

itertoolsを使用した順列の列挙

用意したリスト（my_list）のの中から\( r \)個を並べる場合itertools.permutations(my_list, r)とします。

import itertools

# リストを定義
my_list = ['A', 'B', 'C', 'D']

# itertools.permutationsを使用して順列を列挙
permutations = list(itertools.permutations(my_list, 2))

# 列挙された順列を表示
for perm in permutations:
    print(perm)

# 出力
('A', 'B')
('A', 'C')
('A', 'D')
('B', 'A')
('B', 'C')
('B', 'D')
('C', 'A')
('C', 'B')
('C', 'D')
('D', 'A')
('D', 'B')
('D', 'C')

math.permを使用した順列の総数計算

\( n \)個の中から\( r \)個を並べる場合math.perm(n, r)とします。

例えば、４個の中から２個を並べる場合は次になります。

import math

print(math.perm(4, 2))

# 出力
12

scipy.special.permを使用した順列の総数計算

\( n \)個の中から\( r \)個を並べる場合scipy.special.perm(n, r)とします。

例えば、４個の中から２個を並べる場合は次になります。

import scipy

print(scipy.special.perm(4, 2))

# 出力
12

組合せとは

組合せとは複数のモノを順番関係なく選び出して１組にすること。また、その組の総数のことです。

例：　４つの玉から３つを選ぶ

A、B、C、Dと書かれた球が４個あったとして、その中から３個の球を選ぶ組合せはは何通りになるでしょうか。

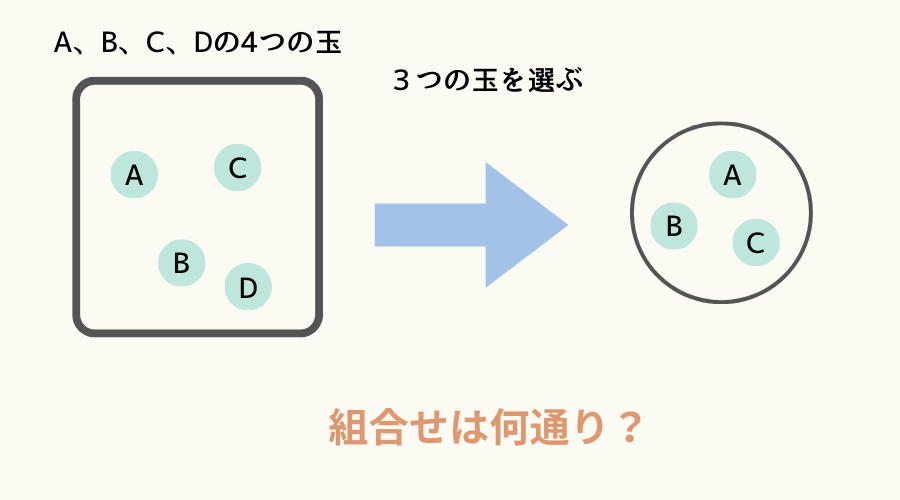
組合せは順列を利用することで計算することができます。

このため、まずは４つの玉の中から３つの玉を並べる順列を考えてみます。

これは、

\( \hspace{10pt} \displaystyle {}_4 \mathrm{P}_3 = 4 \cdot 3 \cdot 2 = 24通り \)

となり、樹形図で表すと次になります。

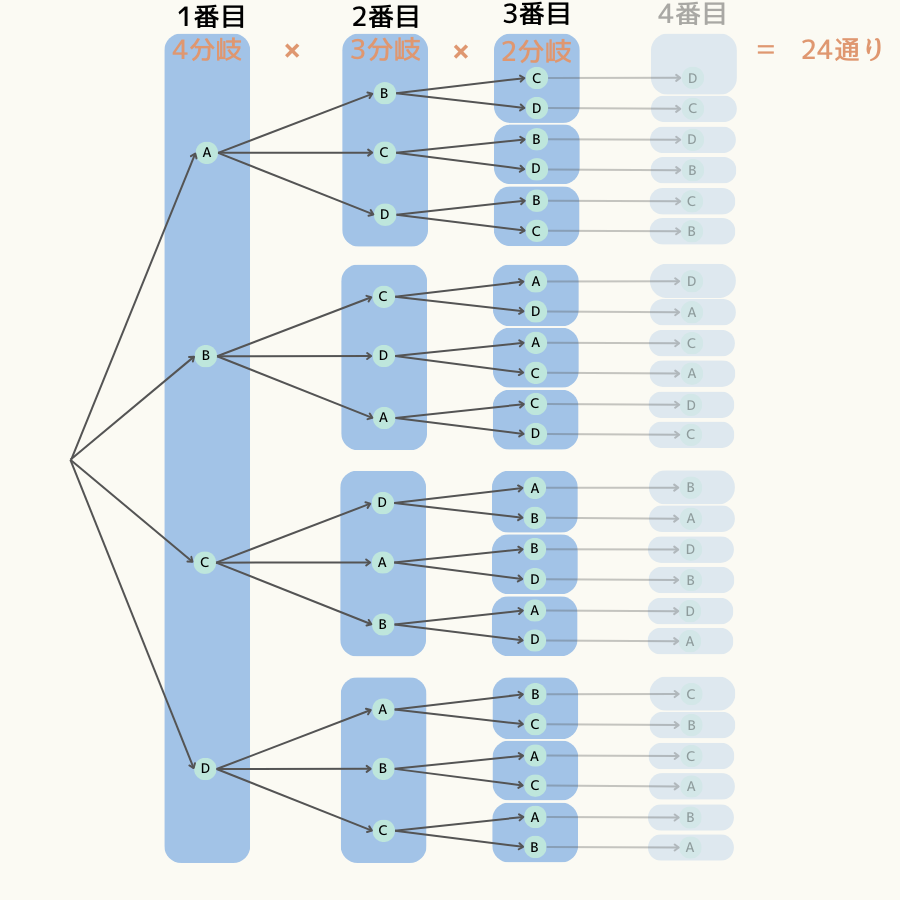
この樹形図は順番も考慮して並べているので、順序を考慮しない組合せの考え方からすると重複があります。

例えば、【A、B、C】の組の場合、次図のように６通りの重複が生じています。

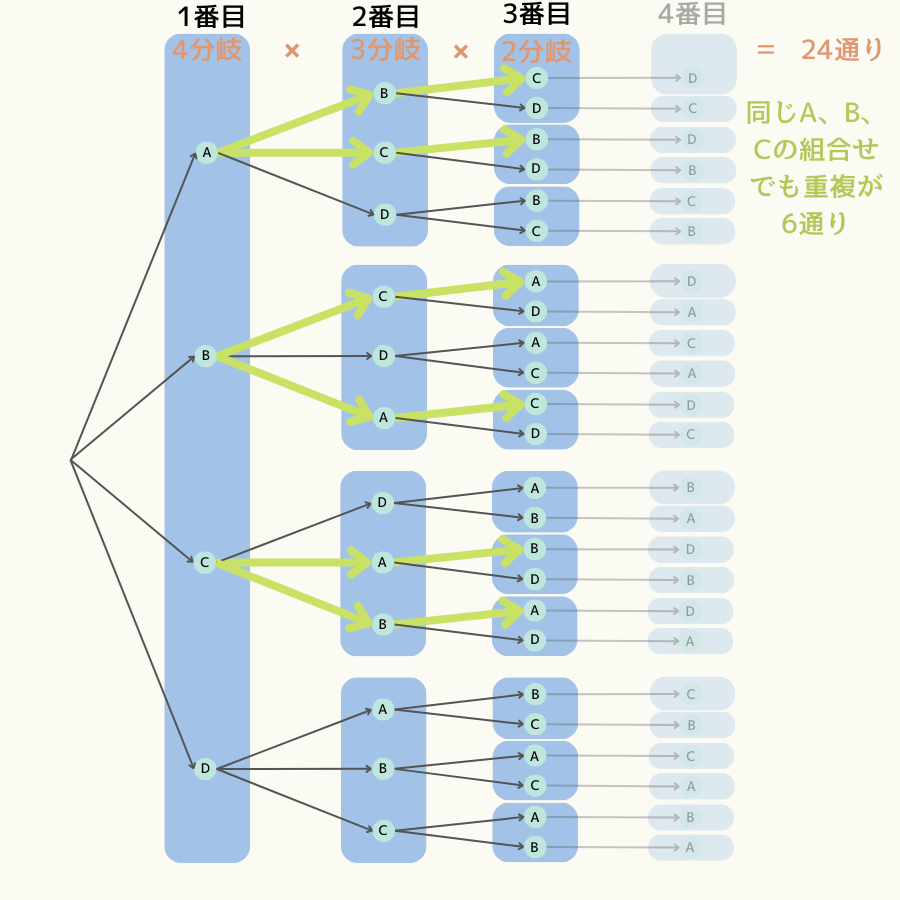
そして、この６通りというのは上のような樹形図を書かずども、【A、B、C】の３つの玉の中から３つを並べる順列\( \displaystyle {}_3 \mathrm{P}_3 = 3 \cdot 2 \cdot 1 = 6 \)より計算できます。

同じことが【A、B、C】以外の組合せ、【A、B、D】、【A、C、D】、【B、C、D】にも同様に言えます。

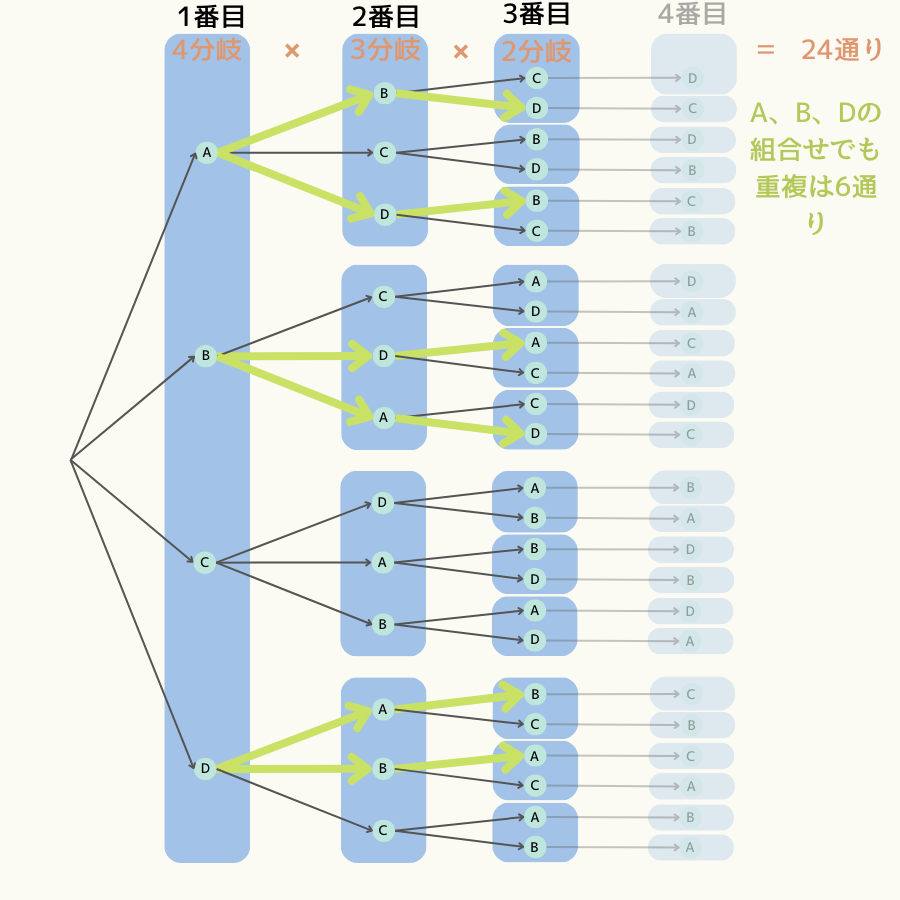
この時点で組合せの総数は４組と答えが出てしまっていますが、組合せの公式を導くため、もう少し話を進めます。

以上のことから、【A、B、C】、【A、B、D】、【A、C、D】、【B、C、D】の４つの組それぞれについて、\( \displaystyle {}_3 \mathrm{P}_3 = 6 \)通りあります。

つまり、この\( {}_4 \mathrm{P}_3（２４通り） \) は\( 「４つの組」 \times {}_3 \mathrm{P}_3 （６通り）\)に分解できます。

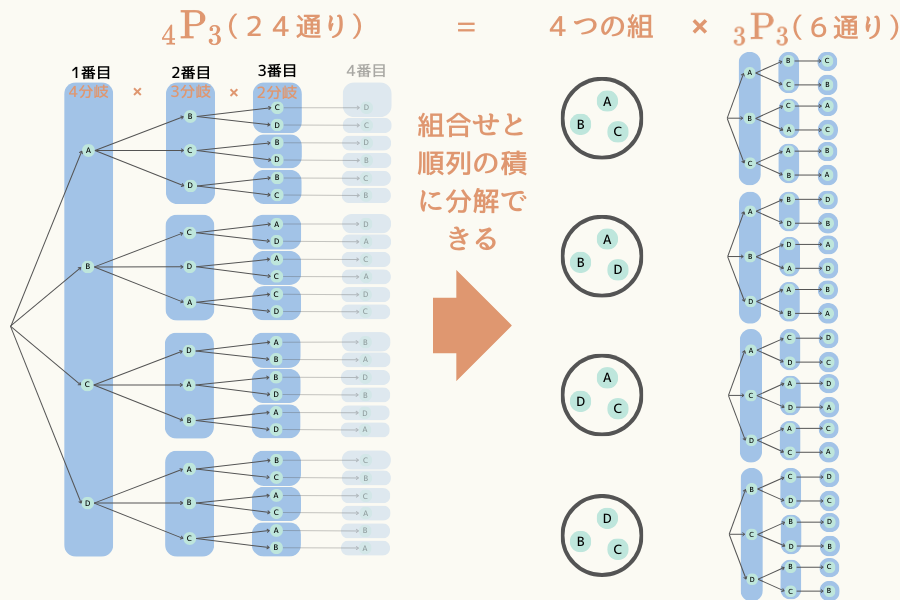
「４つの組」というのはもともと「４つの玉から３つを選ぶ組合せ」でしたから、これに置き換えて数式で表現すると次式となります。

\( \hspace{10pt} \displaystyle {}_4 \mathrm{P}_3 = 「４つの玉から３つを選ぶ組合せ」 \times {}_3 \mathrm{P}_3 \)

この式を「４つの玉から３つを選ぶ組合せ」について、整理すると

\( \hspace{10pt} \displaystyle 「４つの玉から３つを選ぶ組合せ」 = \frac{{}_4 \mathrm{P}_3}{ {}_3 \mathrm{P}_3} \)

と順列を用いて計算できることがわかります。

これを一般化して、

\( \hspace{10pt} \displaystyle 「n個からr個を選ぶ組合せ」 = \frac{{}_n \mathrm{P}_r}{ {}_r \mathrm{P}_r} \)

としたのが下に記載した公式になります。

組合せの公式

\( n \)個の中から\( r \)個を選ぶ組合せは次式となります。
\( \hspace{10pt} \displaystyle {}_n \mathrm{C}_r = \frac{{}_n \mathrm{P}_r}{{}_r \mathrm{P}_r} = \frac{{}_n \mathrm{P}_r}{r!} = \frac{n!}{r!(n-r)!} \)

「\( n \)個の中から\( r \)個を選ぶ組合せ」を\( {}_n \mathrm{C}_r \)と書きます。

また、\( {}_r \mathrm{P}_r = r! \)を使っています。

Pythonによる組合せの計算

itertoolsを使用した組合せの列挙

用意したリスト（my_list）のの中から\( r \)個を組み合わせる場合itertools.combinations(my_list, r)とします。

import itertools

# リストを定義
my_list = ['A', 'B', 'C', 'D']

# itertools.combinationsを使用して順列を列挙
combinations = list(itertools.combinations(my_list, 3))

# 列挙された組合せを表示
for comb in combinations:
    print(comb)

# 出力
('A', 'B', 'C')
('A', 'B', 'D')
('A', 'C', 'D')
('B', 'C', 'D')

math.combを使用した組合せの総数計算

\( n \)個の中から\( r \)個を選ぶ組合せの場合math.comb(n, r)とします。

例えば、４個の中から３個を並べる場合は次になります。

import math

print(math.comb(4, 3))

# 出力
4

scipy.special.combを使用した組合せの総数計算

\( n \)個の中から\( r \)個を選ぶ組合せの場合scipy.special.comb(n, r)とします。

例えば、４個の中から３個を並べる場合は次になります。

import scipy

print(scipy.special.comb(4, 3))

# 出力
4.0

順列と組合せの違い

順列は順序を考慮しますが、組合せは順序を考慮しません。

PやＣは何の略？

• P⇒英語で順列を意味する「Permutation」の頭文字です。
• C⇒英語で組合せを意味する「Combination」の頭文字です。