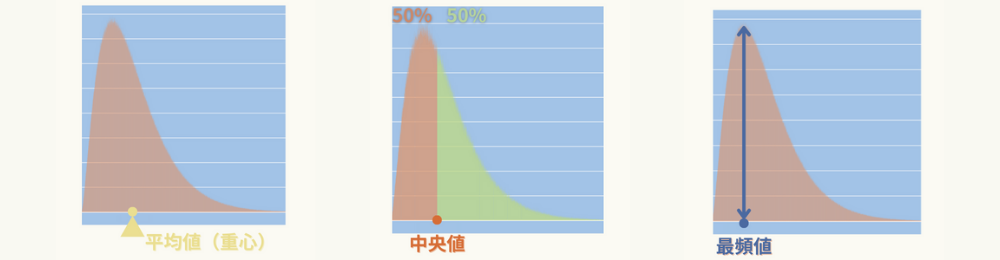
平均値、中央値、最頻値の違い、使い分け
中央値
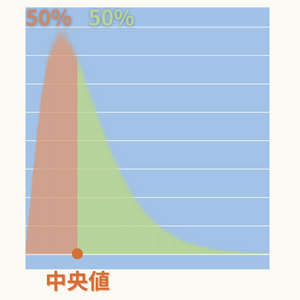
- データの中央の値
- データ分布(ヒストグラム)が半々の面積になる位置
- 外れ値の影響を受けにくい
- データ全体の分布が分かりづらい
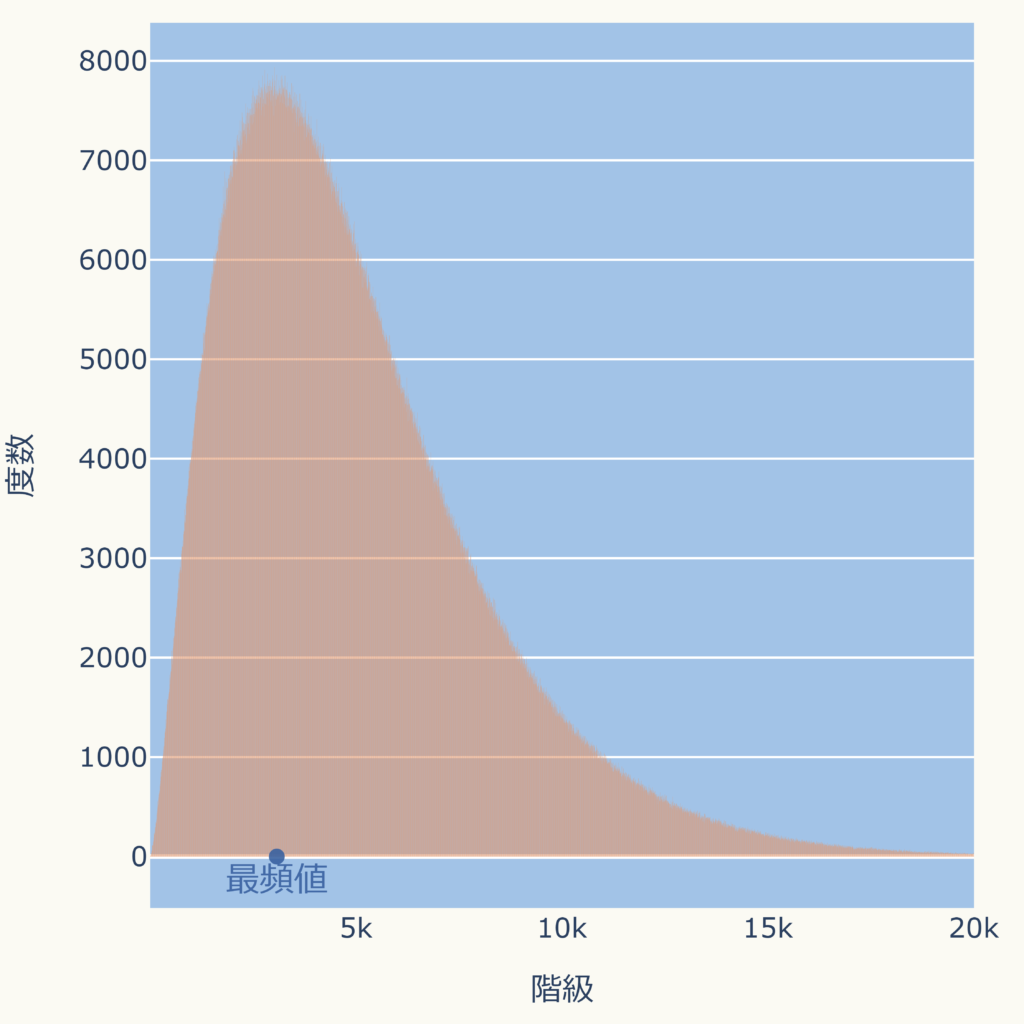
最頻値
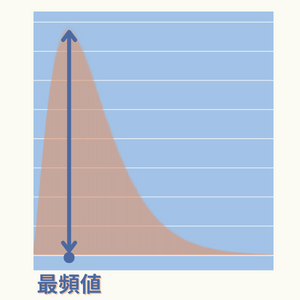
- 最も出現頻度の多いデータ
- データ分布(ヒストグラム)が最も高くなる位置
- 外れ値の影響を受けにくい
- データ全体の分布が分かりづらい
- データ数が少ない場合、位置が定まらない
次にデータ分布(ヒストグラム)を変化させた動画でそれぞれの特徴を見ていきましょう。
(ヒストグラムについいて詳しく知りたい方は「度数分布表とヒストグラム」をご覧ください。)
次の動画は少数のデータがデータの主な分布位置から離れていく場合(外れ値になっていく場合)です。
ちなみに、階級や区間はヒストグラムなどで使われる統計用語です。
階級は区間(1以上2未満といった区間)を表し、度数とはその階級(区間)に含まれるデータの数のことです。
これを見ると平均値は外れ値に引っ張られるように移動しますが、中央値、最頻値は変化しません。
つまり、外れ値の影響を受けづらいです。
ただし、外れ値が計測ミスなどの不要なデータであれば、中央値、最頻値を選ぶ方がいいですが、そうでないなら、中央値、最頻値はデータ全体の分布を反映していないとも言えます。
ちなみに、外れ値のデータが多くなっていく場合はどうなるでしょうか。
平均値は外れ値の分布が増えるに従って、そちらに移動していきます。
中央値も徐々に移動していきますが、外れ値のデータ分布の面積が主たるデータ分布のそれを超えた瞬間(逆転した場合)にそちらにジャンプするように移動します。
中央値や最頻値は平均値と違い、データがあるところにしか存在ません。
また、この動画だと最頻値は変化していませんが、データ数が少ない場合の最頻値は追加データにより位置が変化しやすいです。
以下では平均値、中央値、最頻値の求め方、平均値の物理的な解釈(=重心の位置)について、図を使って視覚的にわかりやすく説明していきます。
平均値とは?(求め方)
平均値とは、データの値を全て足して、それをデータの総数で割ったものです。
具体例で見てみましょう。
例えば9人分の身長データがある場合、平均値は次図になります。
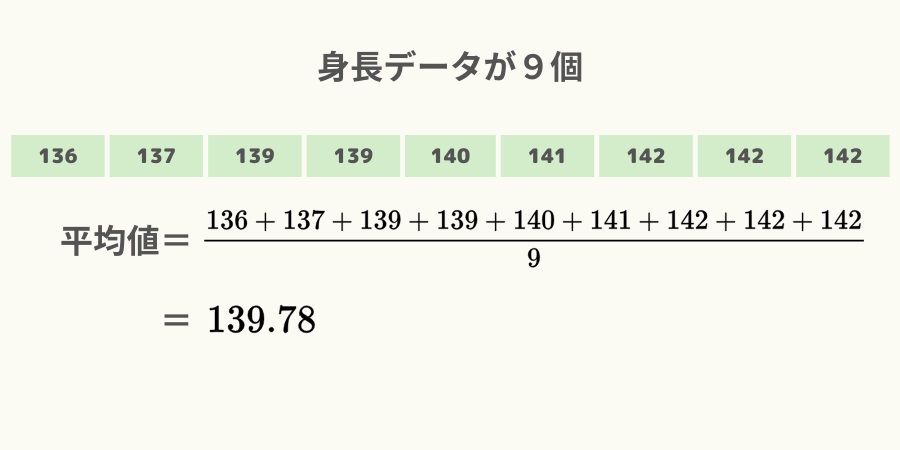
このことを一般化した数式で表現すると次式になります。
\( \hspace{10pt} \displaystyle \bar{x}= \frac{x_{1} + x_{2} + x_{3} \cdots x_{n}}{ n } \)
\( \hspace{20pt} \displaystyle = \frac{ \displaystyle \sum_{i=1}^{n}x_{i} }{ n } \)
\( x_{1} \)や\( x_{2} \)は上の身長の例だと、「136」や「137」といった身長の値です。
また、\( n \)は身長データの数(9個)です。
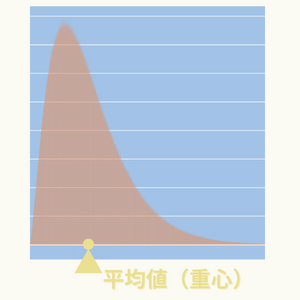
平均値の物理的な解釈 ~ データ分布の重心位置 ~
データの分布を同質量の物の分布と見なした場合、平均値=重心の位置となります。
これが分かると、ヒストグラムなどでデータの分布を見れば、平均値がおよそどのあたりにあるのか感覚的に把握できます。
どういったことなのか、順にみていきましょう。
重心とはその点で物体を支えれば、バランスを崩すことなく支えることができる点です。
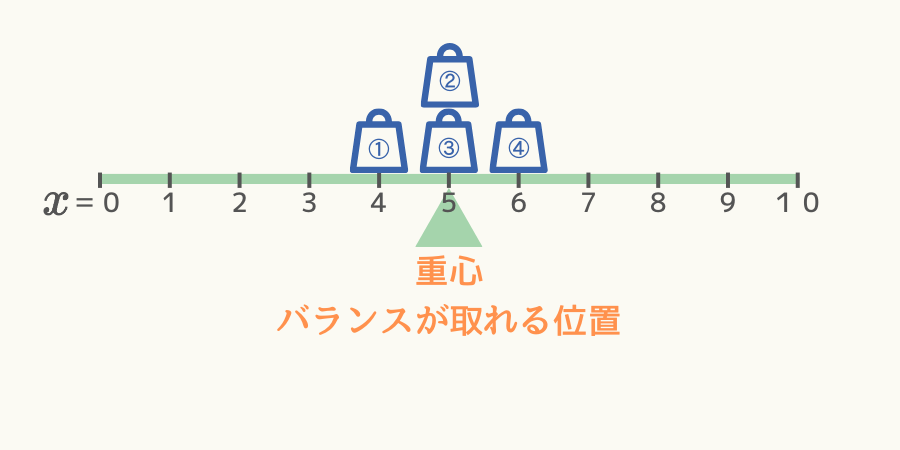
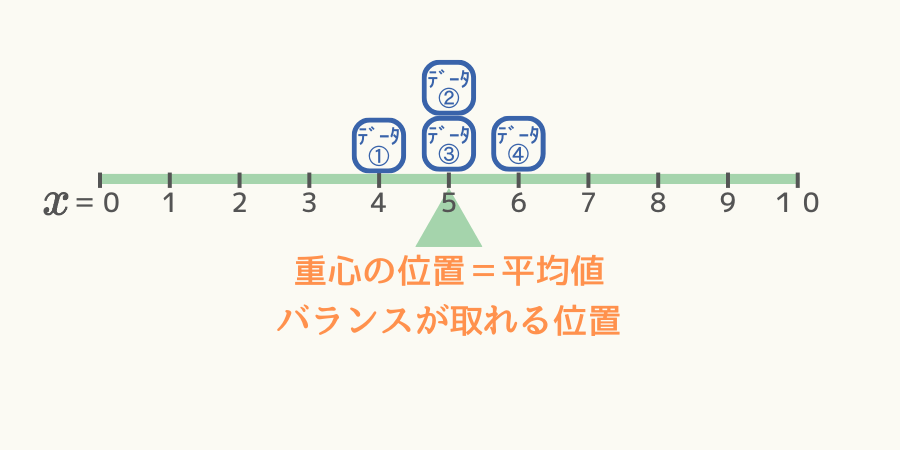
例えば、次図のようにシーソー上に4個重りが分布していた場合、重心の位置は\( x=5 \)の位置です。
(ただし状況を単純化するため、シーソー自体の重さは無いと仮定します。)
次図のようにシーソー上に質量の異なる\( n \)個の重りが分布していた場合、
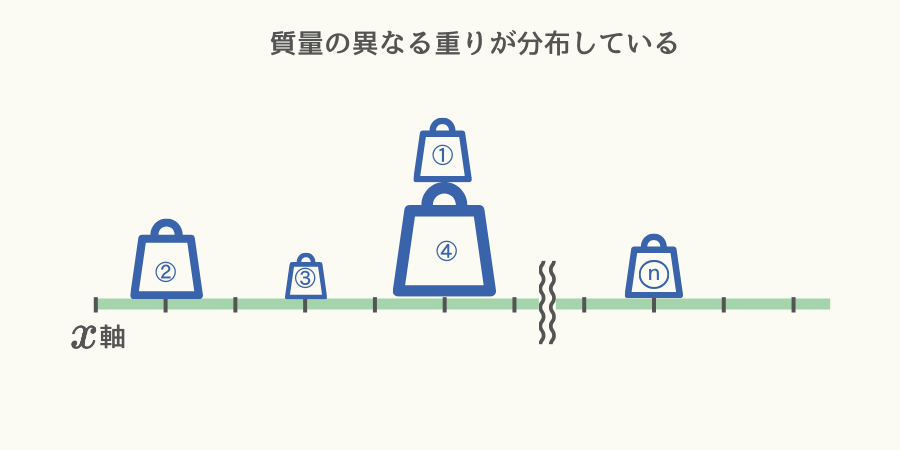
重心の位置を求める式は次になります。
\( \hspace{10pt} \displaystyle 重心の位置 = \frac{m_{1}x_{1} + m_{2}x_{2} + m_{3}x_{3} \cdots m_{n}x_{n}}{m_{1} + m_{2} + m_{3} \cdots m_{n} } \)
\( m_{1} \)などは物体の重さ、\( x_{1} \)などは物体の位置を表しています。
この式において、各物体が同質量\( m \)であった場合は次になります。
\( \hspace{10pt} \displaystyle 重心の位置 = \frac{m x_{1} + m x_{2} + m x_{3} \cdots m x_{n}}{m + m + m \cdots m } \)
\( \hspace{50pt} \displaystyle = \frac{ x_{1} + x_{2} + x_{3} \cdots x_{n}}{ n } \)
\( \hspace{50pt} \displaystyle = \frac{ \displaystyle \sum_{i=1}^{n}x_{i} }{ n } \)
これは上で出てきた平均値を計算する式と同じです。
つまり、データを同一の重さのある物として考えた場合、平均値は重心の位置とイコールになります。
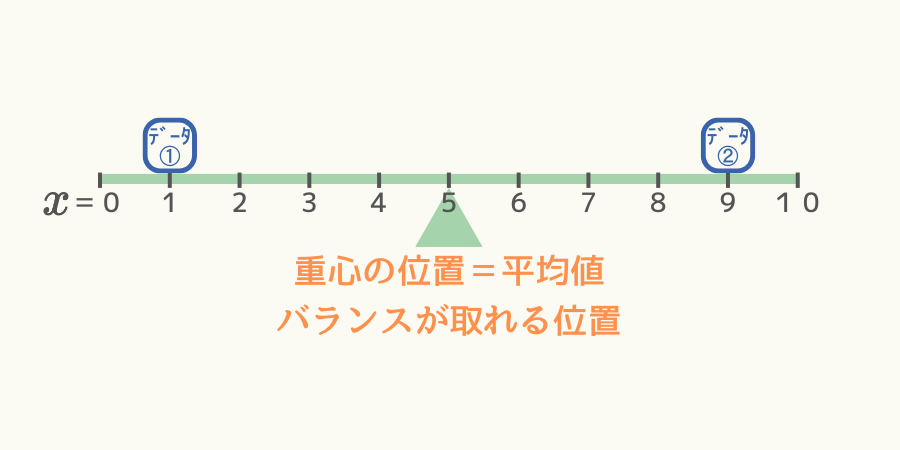
このことから、以下の図のようにデータの分布が分かると感覚的に平均値(重心の位置)が分かる感じがしないでしょうか。
そして、ヒストグラムはデータの個数の分布を見るグラフですので、ヒストグラムを見ると平均値のおよその位置が感覚的に分かると思います。
左右対称の分布の場合、
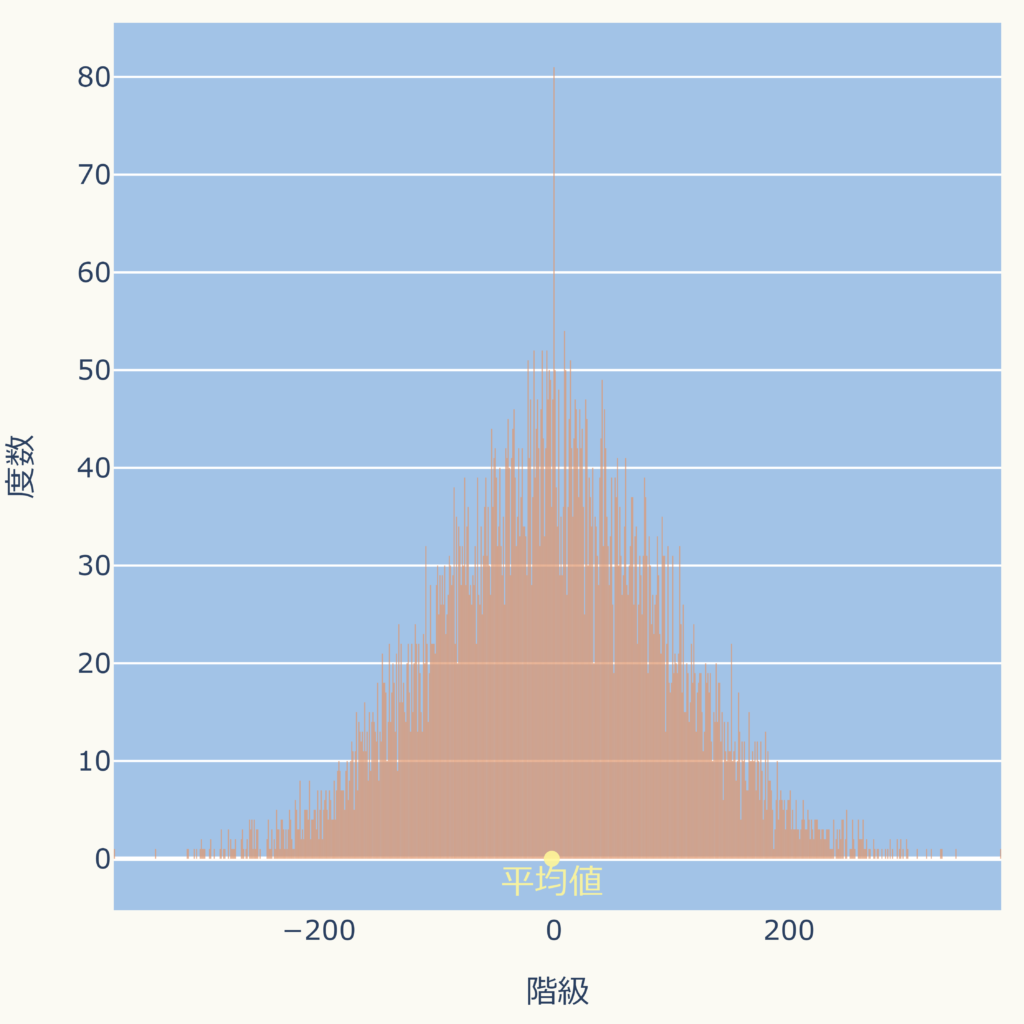
両側に同程度の分布がある場合、
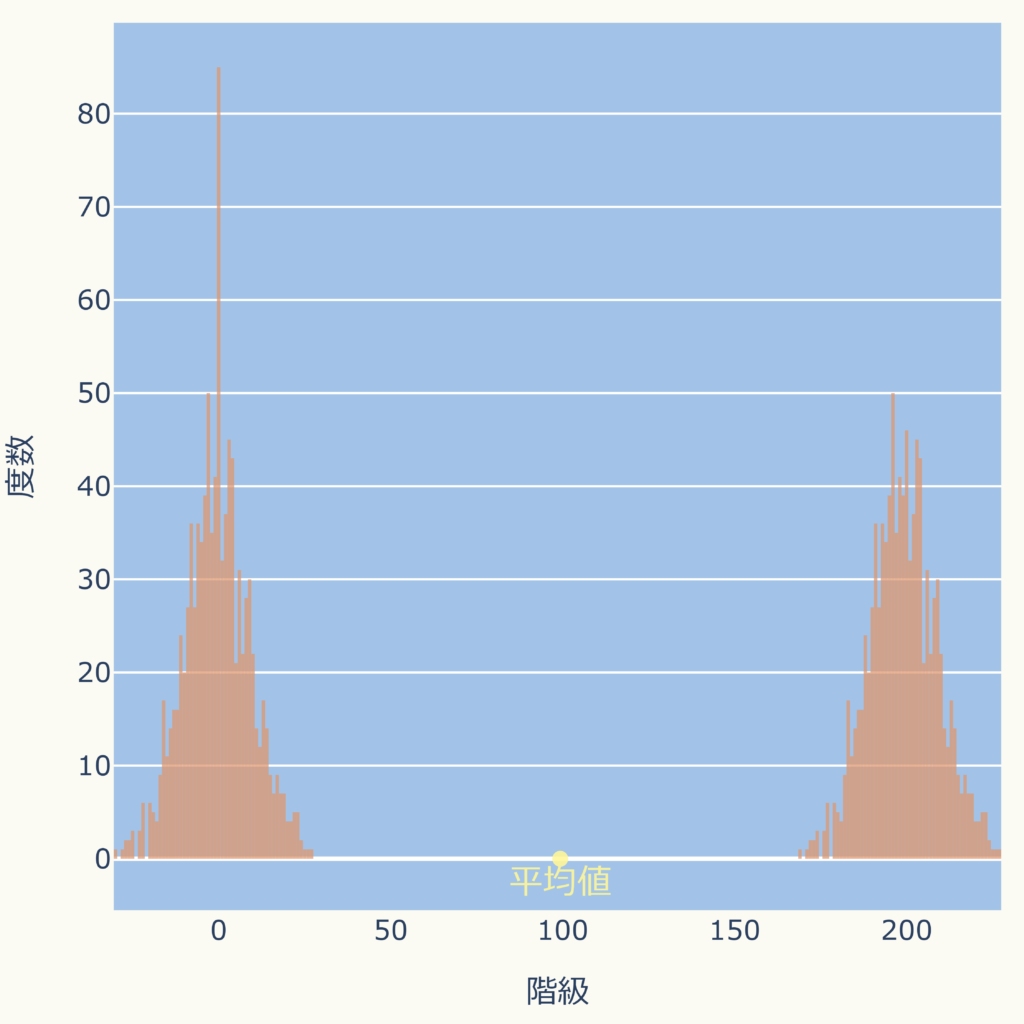
下図のように歪みある分布の場合は平均値が右側に広く分布するデータに引っ張られ、データの最も多い場所からズレます。
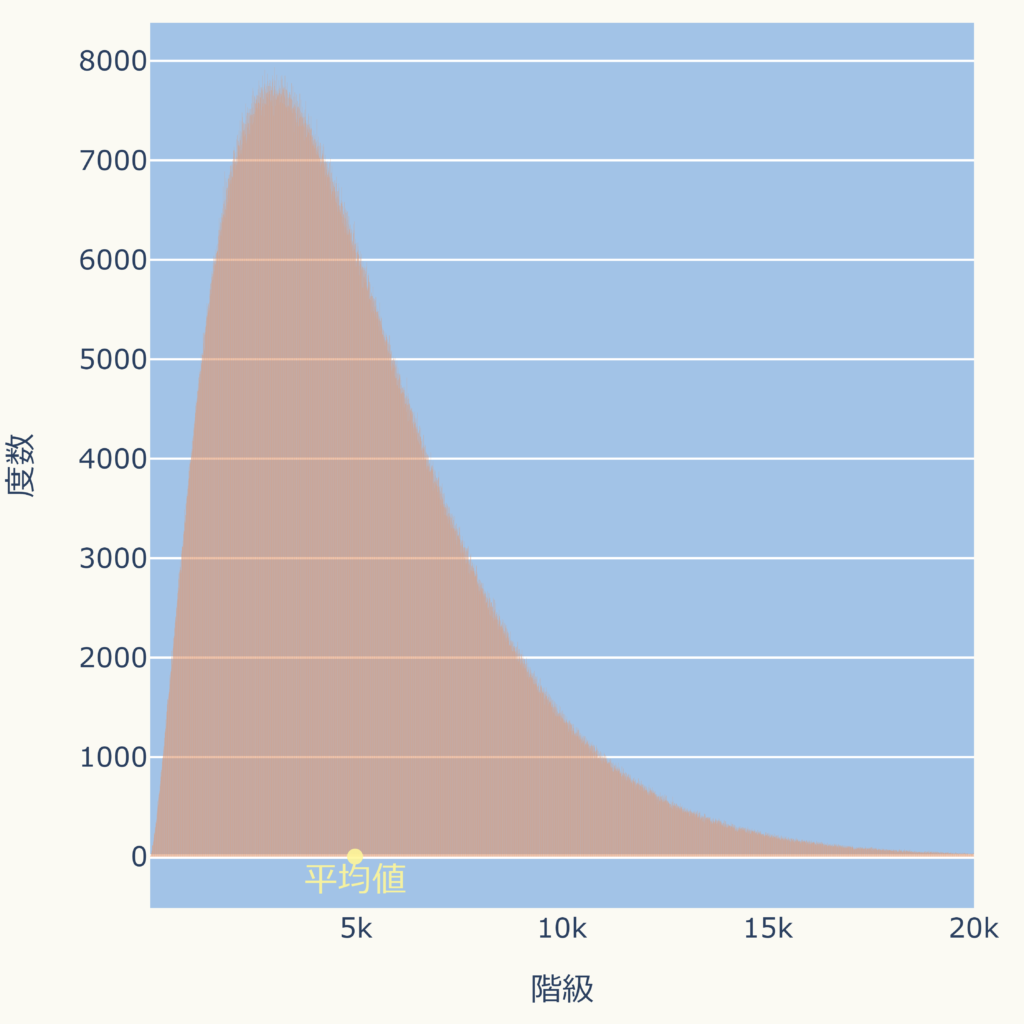
中央値とは?(求め方)
中央値とはデータを順番に並べた場合の中央の値です。
なお、中央の値ですので小さい順、大きい順、どちらで並べても変わりません。
データの数が偶数の場合は中央の値が二つ生じるため、足して2で割ったものを中央値とします。
例えば9人分の身長データ(奇数)がある場合、中央値は次図になります。
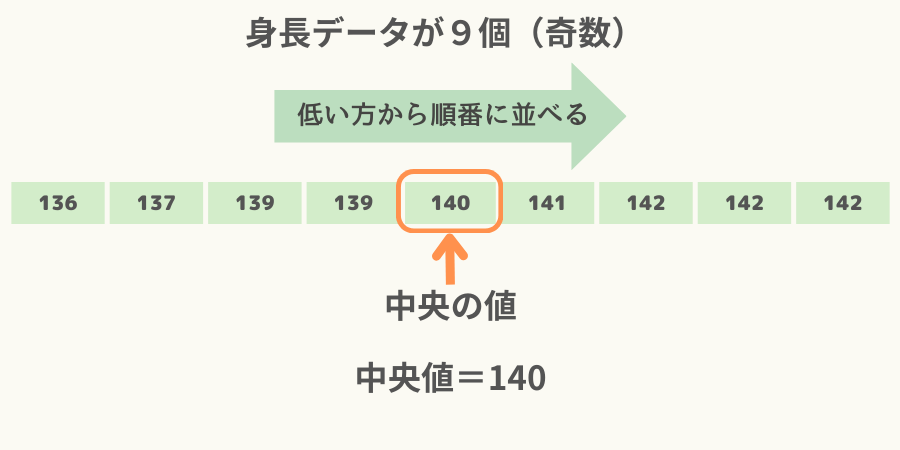
なお、偶数のデータ、例えば10人分の身長データがある場合、平均値は次図のように中央の二つのデータを足して2で割ったものになります。
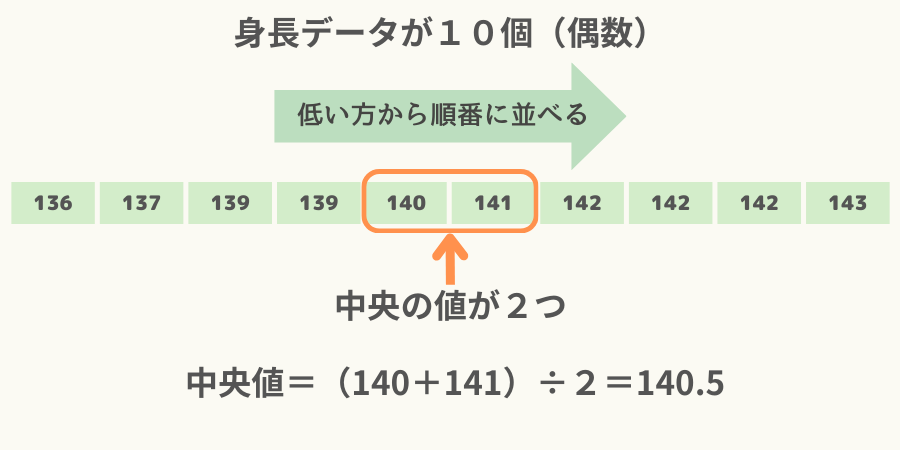
データの個数の分布を表すヒストグラムでは、中央値は面積が半分になる位置です。
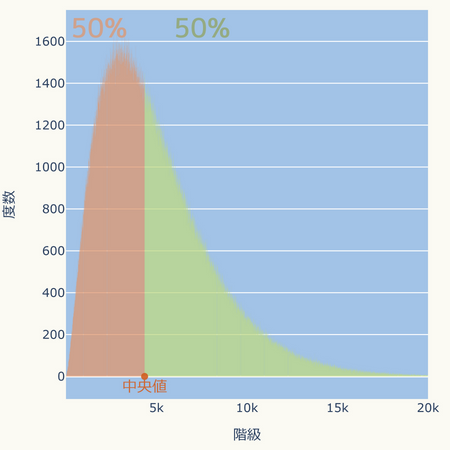
最頻値とは?(求め方)
最頻値とは、最も出現回数の多い値です。
例えば9人分の身長データがある場合、中央値は次図になります。

データの個数の分布を表すヒストグラムでは、グラフが最も高い箇所の値です。