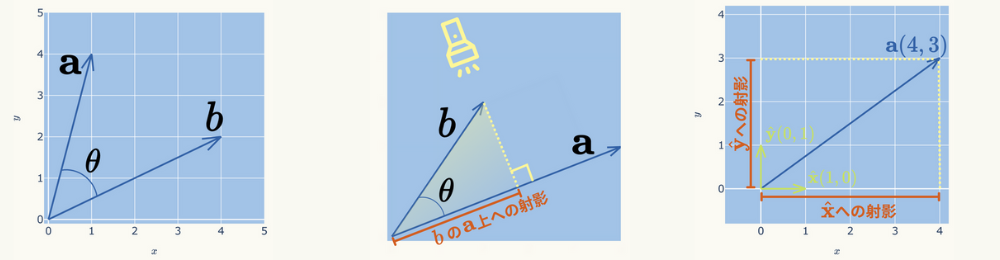
内積とは何か?
内積とは、下図のようにベクトル\( \mathbf{a} \) 、\( \mathbf{b} \)のなす角を\( \theta \)とした場合、次式となります。
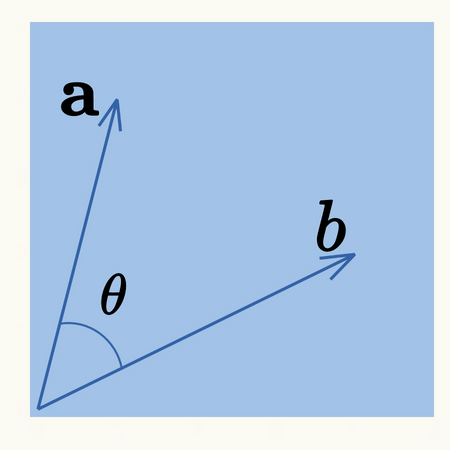
$$ \hspace{10pt} \mathbf{a} \cdot \mathbf{b} = | \mathbf{a} | | \mathbf{b} | \cos \theta $$
\( | \mathbf{a} | \) 、\( | \mathbf{b} | \)はベクトル\( \mathbf{a} \) 、\( \mathbf{b} \)の大きさです。
\( \cos \theta \)に関する式に変形すると、次式となります。
$$ \hspace{10pt} \cos \theta = \frac{\mathbf{a}\cdot \mathbf{b}}{| \mathbf{a} | | \mathbf{b} |} $$
このことから、ベクトル\( \mathbf{a} \) 、\( \mathbf{b} \)が分かれば、そのなす角を計算できます。
成分表示での内積計算
ベクトルの成分表示が\( \mathbf{a} = (a_{1},a_{2}) \)、\( \mathbf{b} = (b_{1},b_{2}) \)の内積\( \mathbf{a} \cdot \mathbf{b} \)の計算は次式となります。
$$ \displaystyle \mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2} $$
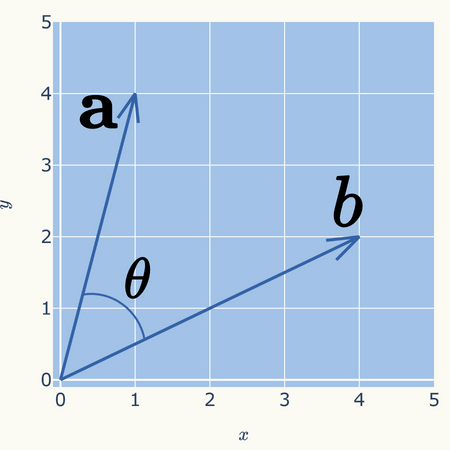
各成分ごとの積の和になります。
ちなみに、三次元の場合(\( \mathbf{a} = (a_{1},a_{2},a_{3}) \)、\( \mathbf{b} = (b_{1},b_{2},b_{3}) \))は次式となります。
\( \hspace{10pt} \displaystyle \mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2}+ a_{3}b_{3} \)
例えば\( \mathbf{a} = (1,4) \)、\( \mathbf{b} = (4,2) \)であれば、
\( \hspace{10pt} \displaystyle \mathbf{a} \cdot \mathbf{b} = 1\times4 + 4\times2 = 12 \)
\( \hspace{10pt} \displaystyle | \mathbf{a} | = \sqrt{1^{2} + 4^{2}} = \sqrt{17} \)
\( \hspace{10pt} \displaystyle | \mathbf{b} | = \sqrt{4^{2} + 2^{2}} = \sqrt{20} = 2\sqrt{5}\)
\( \hspace{10pt} \displaystyle \cos \theta = \frac{\mathbf{a}\cdot \mathbf{b}}{| \mathbf{a} | | \mathbf{b} |} \)
\( \hspace{20pt} \displaystyle = \frac{12}{2\sqrt{85}} \)
Excelなどで\( \cos^{-1} \)(アークコサイン)を計算すると49.3987度くらいになります。
内積の性質
- \( \mathbf{a} \cdot \mathbf{a} = | \mathbf{a} |^{2} \)
- \( \mathbf{a} \cdot (\mathbf{b}+\mathbf{c}) = \mathbf{a} \cdot \mathbf{b}+\mathbf{a} \cdot \mathbf{c} \)
- \( \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} \)
- \( (c\mathbf{a}) \cdot \mathbf{b} = c(\mathbf{a} \cdot \mathbf{b}) = \mathbf{a} \cdot (c\mathbf{b})\)
射影
射影とは、下図のようにイメージ的には、ベクトル\( \mathbf{b} \)からベクトル\( \mathbf{a} \) へ投射された影の長さです。
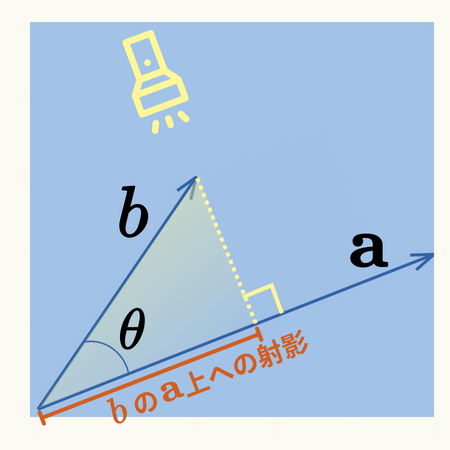
射影は内積を使って、次式で計算できます。
- \( \mathbf{b} \)の\( \mathbf{a} \)上への射影
\( \hspace{10pt} \displaystyle comp_{a}\mathbf{b} = \frac{ \mathbf{a}}{ |\mathbf{a}|}\cdot \mathbf{b} = \hat{ \mathbf{a}} \cdot \mathbf{b} = |\mathbf{b}| \cos \theta\)
なお、\( \hat{\mathbf{a}} \)はベクトル\( \mathbf{a} \)の単位ベクトルです。
これはベクトル\( \mathbf{b} \)のベクトル\( \mathbf{a} \)方向の成分とも言えます。
実際に位置ベクトルの成分表示は基底ベクトルへの射影になります。
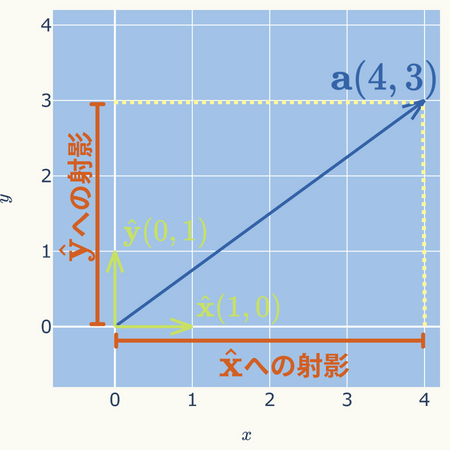
上図の\( \mathbf{a} = (4,3) \)の\( x \)、\( y \)軸への射影を計算してみます。
・\( \hat{ \mathbf{x}} \)への射影
基底ベクトルは大きさ1の単位ベクトルですので、単純に内積を計算することになります。
スマホでご覧の方へ、画面からはみ出す式は横スクロールできます。
\( \hspace{10pt} \displaystyle comp_{ \hat{ \mathbf{x}}}\mathbf{a} = \hat{ \mathbf{x}} \cdot \mathbf{a} = (4,3) \cdot (1,0) = 4\times1 + 3\times0 = 4\)
・\( \hat{ \mathbf{y}} \)への射影
\( \hspace{10pt} \displaystyle comp_{ \hat{ \mathbf{y}}}\mathbf{a} = \hat{ \mathbf{y}} \cdot \mathbf{a} = (4,3) \cdot (0,1) = 4\times0 + 3\times1 = 3\)