度数分布表とは
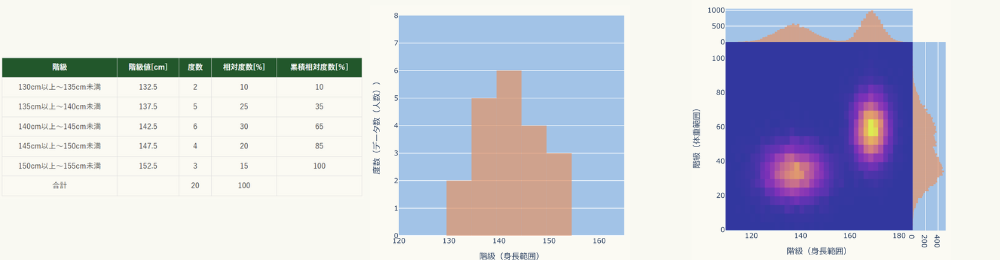
度数分布表とは、データの個数の分布を把握するため、複数あるデータをいくつかの区間(階級と言います)に分割し、それぞれの区間に含まれるデータの個数(度数と言います)を数えて表にしたものです。
例えば、次のような表になります。
| 身長の区間 | データ数(人数) | 全データ数に 占める割合[%] |
|---|---|---|
| 130cm以上~135cm未満 | 2 | 10 |
| 135cm以上~140cm未満 | 5 | 25 |
| 140cm以上~145cm未満 | 6 | 30 |
| 145cm以上~150cm未満 | 4 | 20 |
| 150cm以上~155cm未満 | 3 | 15 |
| 合計 | 20 | 100 |
各身長区間ごとのデータ数(人数)が整理されているため、データ数の分布が分かりやすくなります。
度数分布表の作り方
具体例で度数分布表の作り方を見てみましょう。
生徒の身長がデータとして与えられたとして、度数分布表を作成してみます。
身長データ(20人分)[単位はcm]
| 151 | 141 | 145 | 154 | 152 |
| 130 | 145 | 136 | 137 | 141 |
| 139 | 149 | 143 | 139 | 141 |
| 140 | 149 | 136 | 140 | 131 |
このデータを身長の低い方から順番に並べます。
そしていくつかの区間に分割して、各区間内のデータ数を数え上げます。
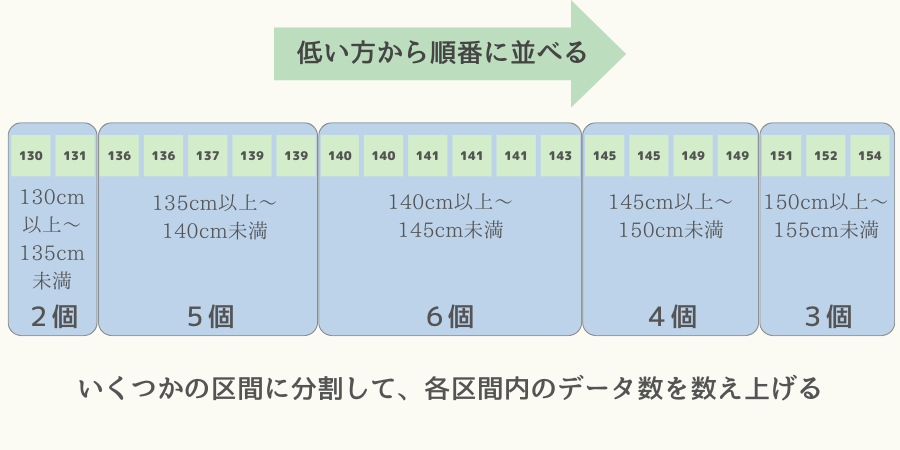
これを表にしたものが次の度数分布表です。
| 身長の区間 | データ数 | 全データ数に 占める割合[%] |
|---|---|---|
| 130cm以上~135cm未満 | 2 | 10 |
| 135cm以上~140cm未満 | 5 | 25 |
| 140cm以上~145cm未満 | 6 | 30 |
| 145cm以上~150cm未満 | 4 | 20 |
| 150cm以上~155cm未満 | 3 | 15 |
| 合計 | 20 | 100 |
統計用語:階級、階級値、度数、相対度数、累積相対度数
統計の分野ですと、先程の身長の度数分布表の「身長の区間」などは次の用語で表現されます。
- 階級 :各区間のこと(身長の例だと、「130cm以上~135cm未満」など)
- 度数 :各区間に含まれるデータ数
- 相対度数 :全データに占める割合
また、階級値、累積相対度数といった用語も使われることがあります。
- 階級値 :階級の真ん中の値、中央値(階級が「130cm以上~135cm未満」であれば、中央値は132.5cm)
- 累積相対度数 :その階級までの全ての相対度数の和(身長の例だと、階級が「135cm以上~140cm未満」の累積相対度数は、「130cm以上~135cm未満」の相対度数10%+「135cm以上~140cm未満」の相対度数25%=35%)
以上の統計用語を使用すると、先程の身長の度数分布表は次になります。
| 階級 | 階級値[cm] | 度数 | 相対度数[%] | 累積相対度数[%] |
|---|---|---|---|---|
| 130cm以上~135cm未満 | 132.5 | 2 | 10 | 10 |
| 135cm以上~140cm未満 | 137.5 | 5 | 25 | 35 |
| 140cm以上~145cm未満 | 142.5 | 6 | 30 | 65 |
| 145cm以上~150cm未満 | 147.5 | 4 | 20 | 85 |
| 150cm以上~155cm未満 | 152.5 | 3 | 15 | 100 |
| 合計 | 20 | 100 |
度数分布表とヒストグラムの違い
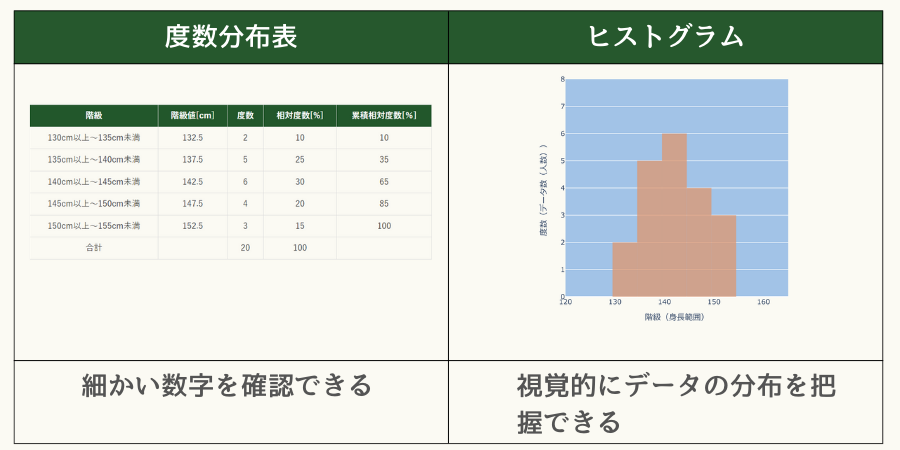
度数分布表をグラフ化したものをヒストグラムと言います。
グラフ化することで、視覚的にデータの分布を把握できます。
逆に度数分布表では細かい数字を確認できます。
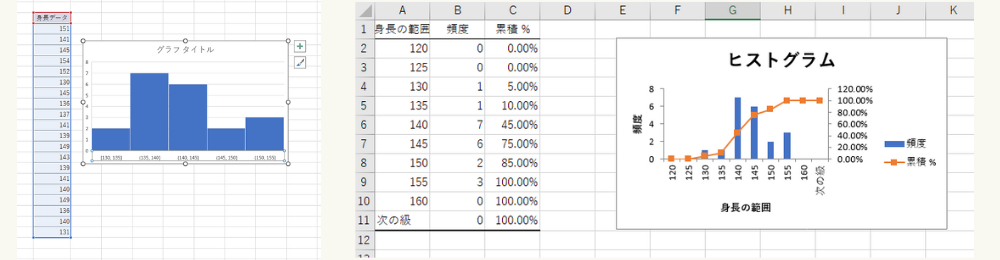
Excelによる度数分布表の作り方
Excelによる度数分布表の作り方については次の記事をご覧ください。
ヒストグラムとは
ヒストグラムとは、度数分布表の階級を横軸、度数を縦軸としてグラフ(一般に棒グラフ)化したものです。
例えば、先の身長の例では次図のようになります。
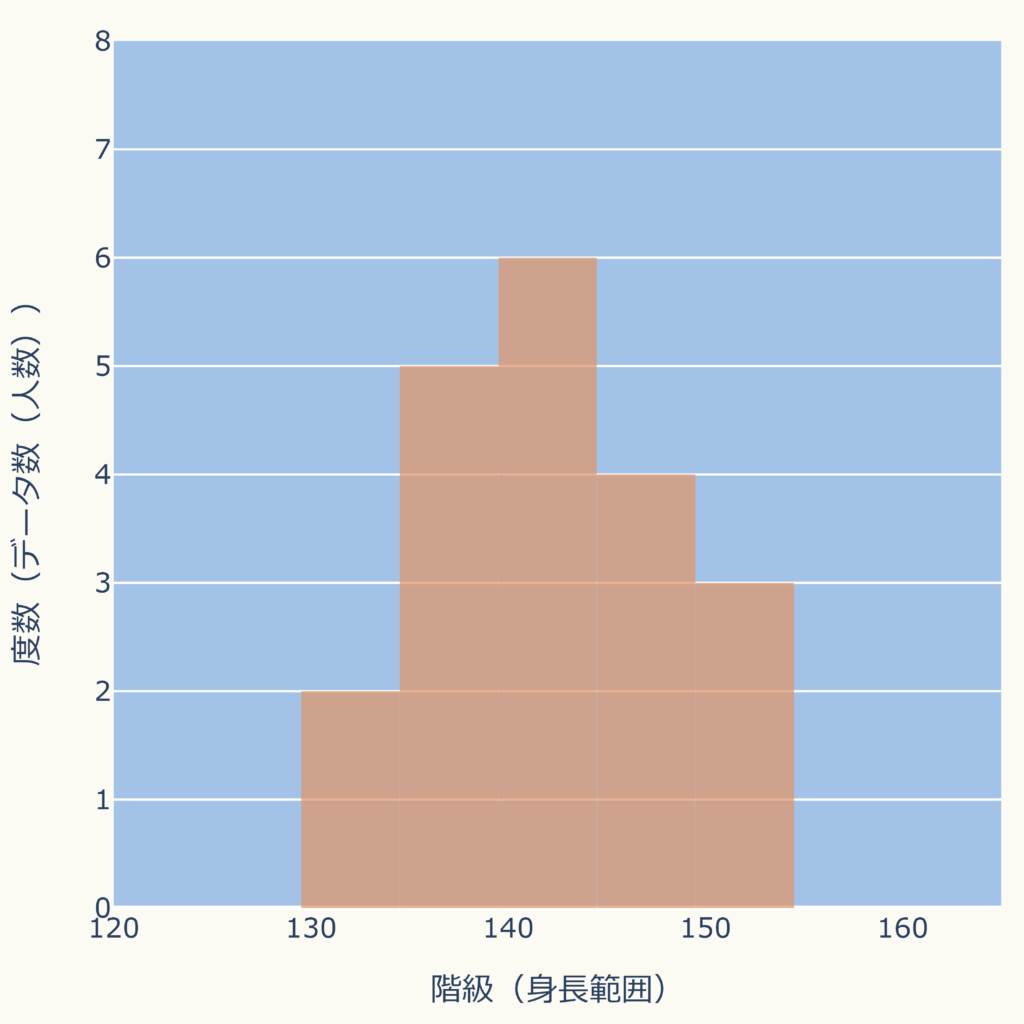
データ数(人数)の分布がパッと分かるようになりますね。
ヒストグラムの見方
ヒストグラムの概形別にその特徴をみていきます。
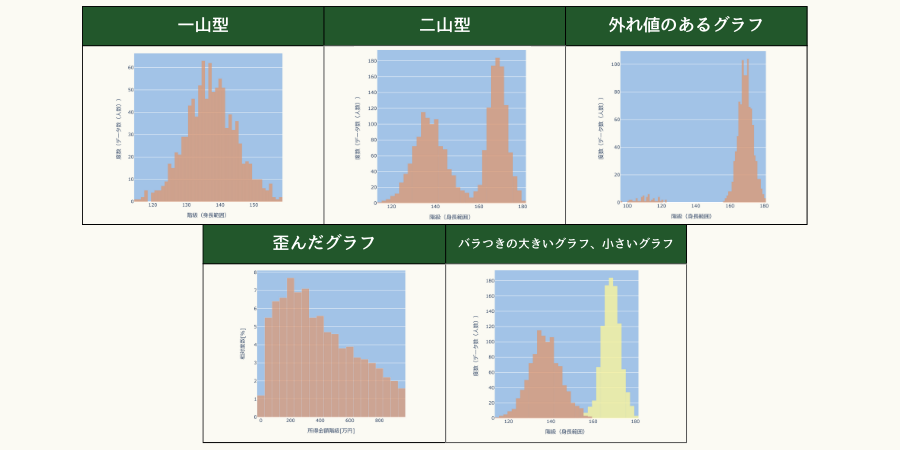
一山型
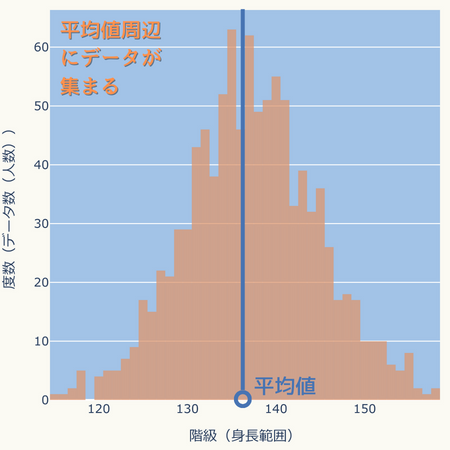
データが平均値周辺に集まり、左右対称に分布したものです。
身長や体重、テストの点数などにみられるといわれます。
平均値付近のデータが多いので、平均値が当該データの特徴をよく表す値となります。
例えば、平均身長が分かればその身長付近の人が多いことが分かります。
二山型
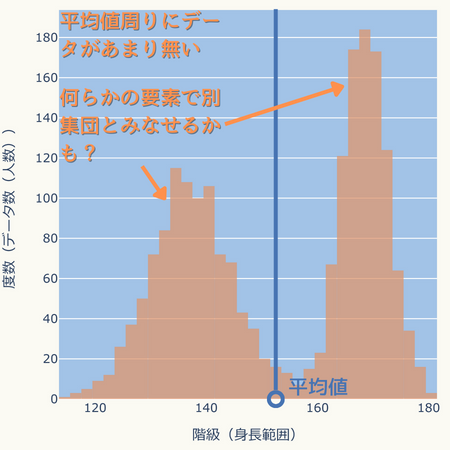
平均値は二つの山の中間にあるため、平均値周辺にデータがあまりありません。
このため、平均値身長が分かってもその身長付近の人が多いとはなりません。
また、何らかの要素で別集団とみなせる可能性があります。
実は、上の図は10歳と15歳の身長データを区別せずヒストグラムにしたものです。
(データは国の身長に関する統計情報(平均値など)を基に作成した疑似データです)
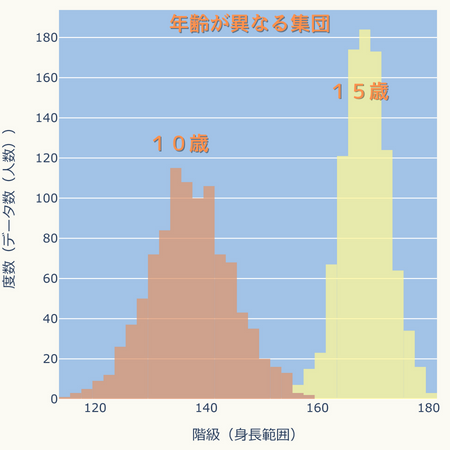
区別すれば次図となります。
外れ値のあるグラフ
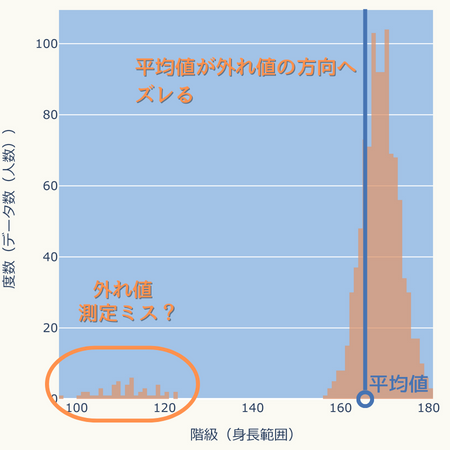
上図のような離れたところにちょこっとあるデータは外れ値と呼び、測定ミスなどの可能性があります。
また、外れ値の影響を受けて平均値が外れ値の方向へズレてしまいます。
歪んだグラフ
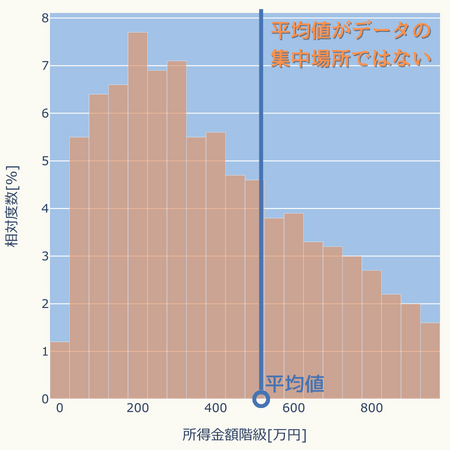
左右対称ではないグラフです。
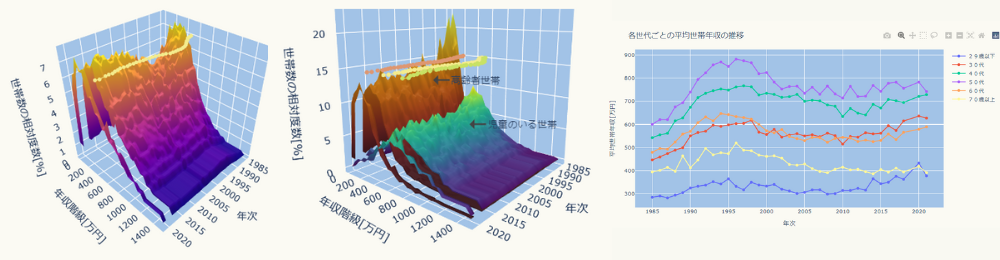
上図はデータが右側に広く分布しているため平均値がデータの集中場所からズレてしまっています。
この図は「令和4年国民生活基礎調査」の調査結果から作った世帯年収(所得金額)別の世帯数の割合(相対度数)です。
世帯年収の平均は約546万円ですが、世帯数が多いのは200万円付近となっています。
バラつきの大きいグラフ、小さいグラフ

15歳より10歳の方がデータ分布が広がっています。
このことから、10歳の方が身長のバラつきが大きいことがわかります。
棒グラフとヒストグラムの違い
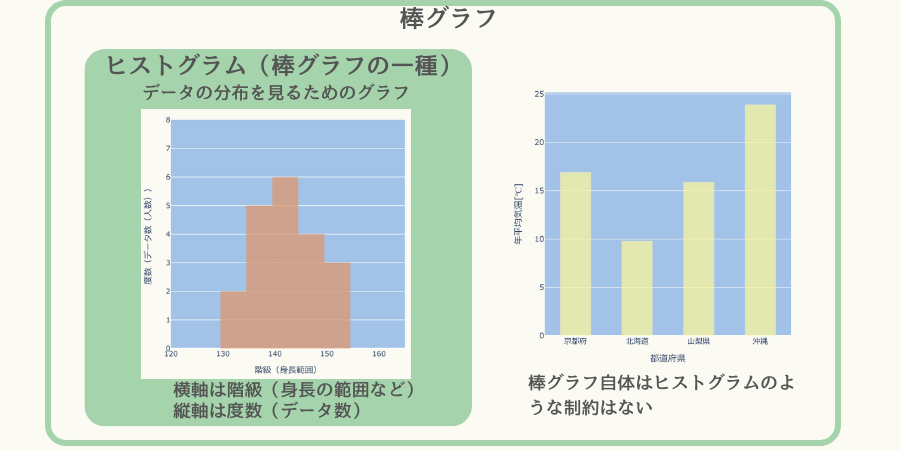
ヒストグラムは棒グラフの一種です。
ただ、目的がデータの分布を見るためのグラフであるため、横軸は階級(順番のある数値を適当な範囲に区切ったモノ、例えば身長の範囲など)、縦軸は度数(データ数)になります。
棒グラフ自体はそのような制約がなく、例えば横軸に都道府県の名前(順番のある数値ではない)、縦軸に平均気温といったものでもOKです。
Excelによるヒストグラムの作り方
Excelによるヒストグラムの作り方については次の記事をご覧ください。

Pythonによるヒストグラムの作り方
Pythonによるヒストグラムの作り方として「matplotlib」、「plotly」、「pandas」3つのライブラリを使用した方法を紹介します。
個人的なおすすめとしては、グラフをちゃんと作るなら「plotly」、pandasでデータ分析している時にサッと確認したいなら「pandas」の方法かなと思います。
「plotly」で作成したグラフはマウスを上に持っていくと具体のデータの値が分かるなどインタラクティブなグラフですので、データ分布をグラフで視覚的に把握しつつ、細かいデータも確認できます。
matplotlibを使用したヒストグラムの作り方
import matplotlib.pyplot as plt
# 身長データ
data = [151, 141, 145, 154, 152, 130, 145, 136, 137, 141, 139, 149, 143, 139, 141, 140, 149, 136, 140, 131]
# ヒストグラムを作成 棒の数をbinsで設定
plt.hist(data, bins=5, edgecolor='black')
# グラフにタイトルとラベルを追加
plt.title('Histogram')
plt.xlabel('height')
plt.ylabel('Number of people')
# ヒストグラムを表示
plt.show()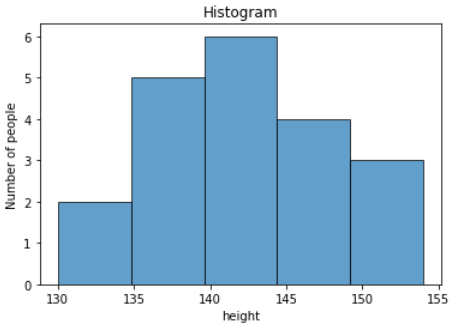
plotlyを使用したヒストグラムの作り方
import plotly.express as px
# 身長データ
data = [151, 141, 145, 154, 152, 130, 145, 136, 137, 141, 139, 149, 143, 139, 141, 140, 149, 136, 140, 131]
# ヒストグラムを作成 棒の数をbinsで設定
fig = px.histogram(data, nbins=10)
# グラフにx軸とy軸のラベルを設定
fig.update_layout(
title='Histogram',
xaxis_title='height',
yaxis_title='Number of people'
)
# 凡例を非表示にする
fig.update_traces(showlegend=False)
# グラフを表示
fig.show()
pandasを使用したヒストグラムの作り方
import pandas as pd
# 身長データ
data = [151, 141, 145, 154, 152, 130, 145, 136, 137, 141, 139, 149, 143, 139, 141, 140, 149, 136, 140, 131]
# データをPandasのSeriesに変換する
data_series = pd.Series(data)
# ヒストグラム作成 棒の数をbinsで設定
data_series.plot.hist(bins= 5)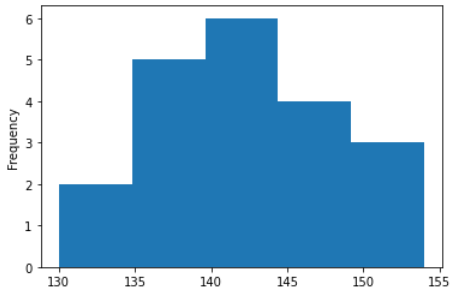
2次元のヒストグラムとは
2次元のヒストグラムとは、[身長、体重]のように変数が2種類ある場合のデータ分布を見るためのグラフです。
例えば、次図のようになります。
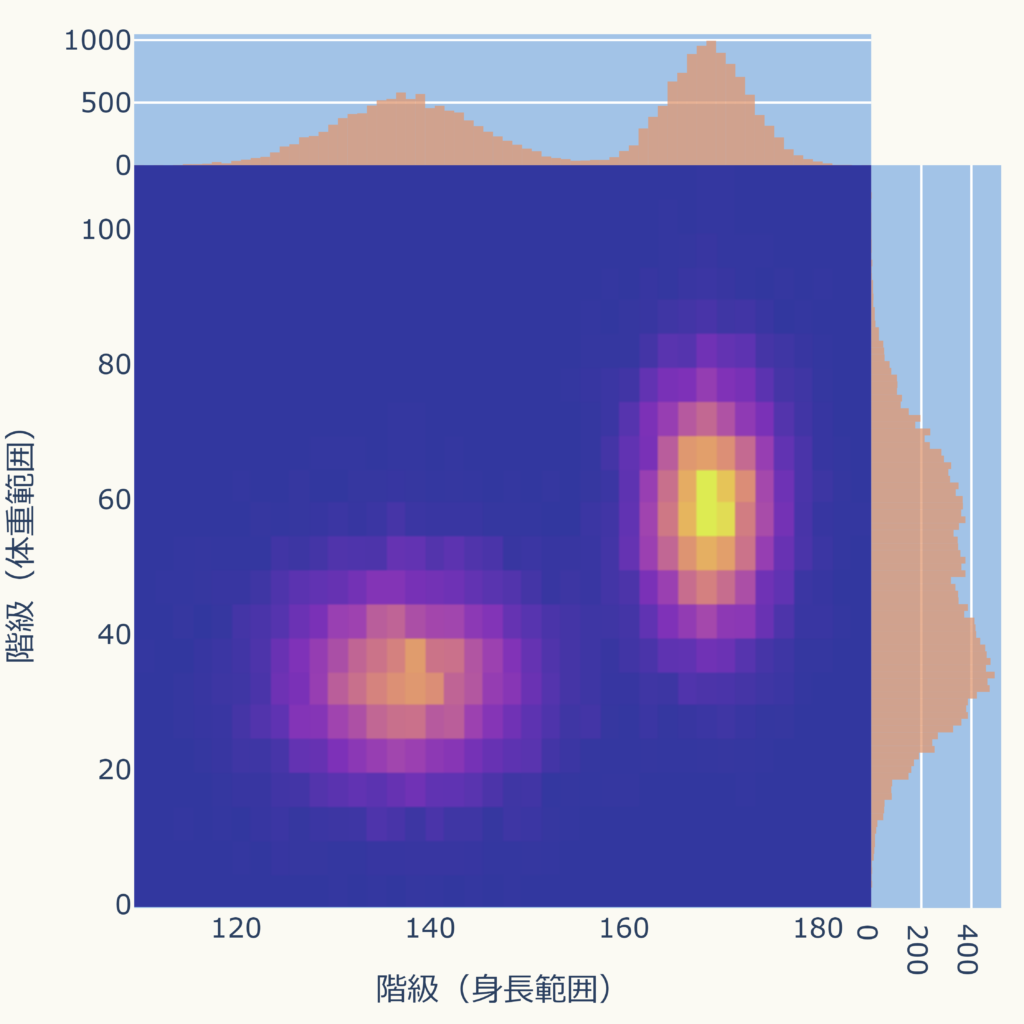
色の違いでデータ分布を表現しています。
明るい箇所がデータが集中している所です。
参考に1次元のヒストグラムも上と右側に表示しました。
もしグラフをドラッグで回転できるとしたら、次のような3D表示も山の高さが分かりやすいと思います。
(このグラフは回転できます)
Pythonによる2次元ヒストグラムの作り方
Pythonによる2次元ヒストグラムの作り方として「matplotlib」ライブラリ、「plotly」ライブラリの「 Histogram2d」、「Surface」3つの方法を紹介します。
matplotlibを使用した2次元ヒストグラムの作り方
import numpy as np
import matplotlib.pyplot as plt
# 乱数を生成して2つのデータセットを作成します
np.random.seed(0)
x = np.random.randn(1000)
y = np.random.randn(1000)
# ヒストグラムを作成します
plt.hist2d(x, y, bins=(50, 50), cmap=plt.cm.jet)
plt.colorbar()
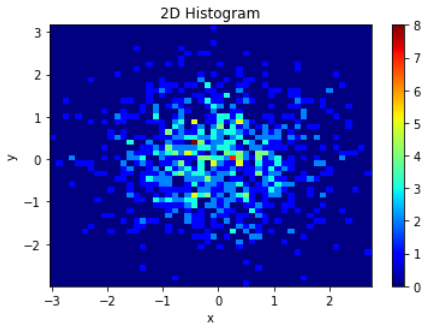
plt.xlabel('x')
plt.ylabel('y')
plt.title('2D Histogram')
plt.show()
plotly Histogram2dを使用した2次元ヒストグラムの作り方
import numpy as np
import plotly.graph_objects as go
# 乱数を生成して2つのデータセットを作成します
np.random.seed(0)
x = np.random.randn(1000)
y = np.random.randn(1000)
# ヒストグラムを作成します
fig = go.Figure()
fig.add_trace(go.Histogram2d(
x=x,
y=y,
nbinsx=40,
nbinsy=40,
))
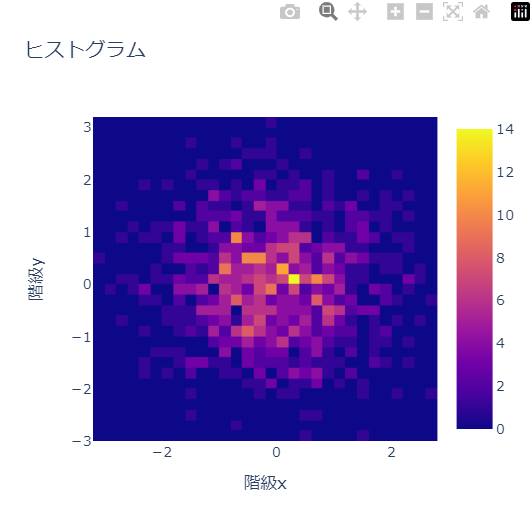
fig.update_layout(
title_text='ヒストグラム', # title of plot
xaxis_title_text='階級x', # xaxis label
yaxis_title_text='階級y', # yaxis label
width= 450,height= 450,
)
fig.show()
plotly Surfaceを使用した2次元ヒストグラムの作り方
import numpy as np
import plotly.graph_objects as go
# 乱数を生成して2つのデータセットを作成します
np.random.seed(0)
x = np.random.randn(1000)
y = np.random.randn(1000)
# 2次元度数分布表を作成
hist, x_edges, y_edges = np.histogram2d(x, y, bins=(10, 10))
# X座標とY座標のグリッドを作成
x, y = np.meshgrid(x_edges, y_edges)
# 3D Surfaceプロットを作成
fig = go.Figure(data=[go.Surface(z=hist.T, x=x, y=y)])
fig.update_layout(scene=dict(zaxis_title='度数',
xaxis_title='階級x',
yaxis_title='階級y',))
fig.update_layout(title='2Dヒストグラム')
fig.update_layout(
width= 450,height= 450,
)
fig.show()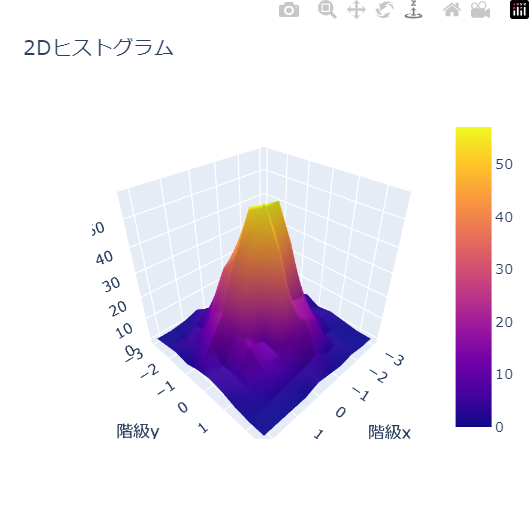
実践例
3Dグラフで見る世帯年収の分布と平均の推移