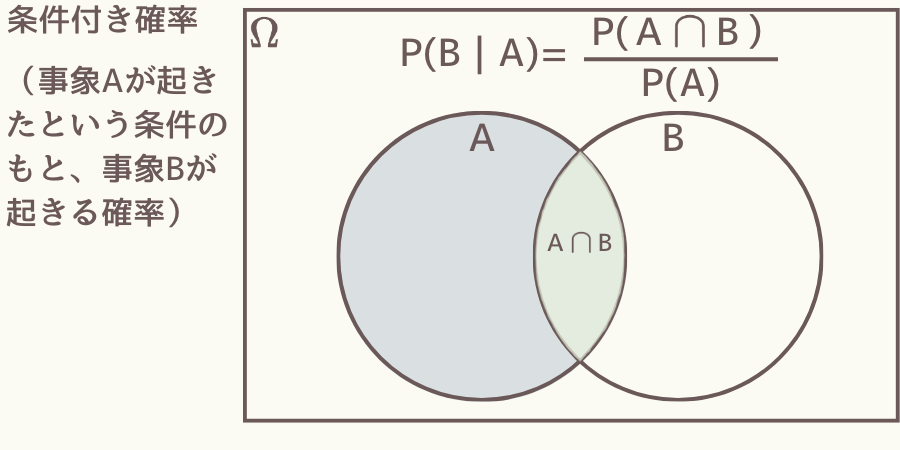
条件付き確率
事象Aの下での事象Bの条件付き確率とは、事象Aが起きたという条件のもと事象Bが起きる確率です。
条件付き確率は次式で計算できます。
\( \hspace{10pt} \displaystyle P(B | A) = \frac{P(A \cap B)}{P(A)} \)
一般に\( P(A) \)は全事象の一部の事象の確率なので\( 0 < P(A) < 1\)ですので、上の式の右辺は分母が1より小さくなります。
よって、
\( \hspace{10pt} \displaystyle P(B | A) > P(A \cap B) \)
となり、\( P(B | A) \)の方が\( P(A \cap B) \)より大きくなります。
これは事象Aが起きたという条件によって、考慮する範囲が全事象\( \Omega \)から事象Aの範囲に縮小されたことによります。
具体例で見てみましょう。
例えばサイコロ振りの場合、事象「奇数の目」の下での「4以上の目」の条件付き確率は次図になります。
ただし、各目の出る確率は同じとします。
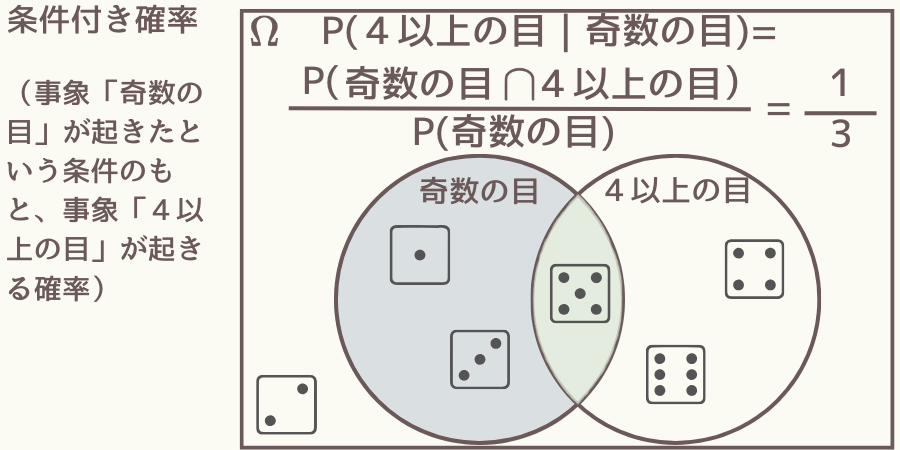
条件付き確率は
\( \hspace{10pt} \displaystyle P(4以上の目 | 奇数の目) = \frac{P(奇数の目 \cap 4以上の目)}{P(奇数の目)} \)
ですので、\( P(奇数の目) \)と\( P(奇数の目 \cap 4以上の目) \)を求めます。
各目の出る確率が同じ場合、各事象の確率は注目している結果と可能な全ての結果の比で求められるので、
\( \hspace{10pt} \displaystyle P(奇数の目) = \frac{3(奇数の目)}{6(可能な全ての結果)} \)
\( \hspace{20pt} \displaystyle = \frac{1}{2} \)
\( \hspace{10pt} \displaystyle P(奇数の目 \cap 4以上の目) \)
\( \hspace{20pt} \displaystyle = \frac{1(5の目)}{6(可能な全ての結果)} \)
となり、条件付き確率は
\( \hspace{10pt} \displaystyle P(4以上の目 | 奇数の目) = \frac{P(奇数の目 \cap 4以上の目)}{P(奇数の目)} \)
\( \hspace{20pt} \displaystyle = \frac{\frac{1}{6}}{\frac{1}{2}} = \frac{1}{3}\)
です。
しかし、これは上図を見ても分かるように、「奇数の目」が出たという条件あることによって、「可能な全ての結果」が6⇒3に縮小したことにより
\( \hspace{10pt} \displaystyle P(4以上の目 | 奇数の目) = \frac{1(5の目)}{3(縮小された可能な全ての結果:1、3、5の目)} \)
\( \hspace{20pt} \displaystyle = \frac{1}{3}\)
と計算することもできます。
排反な事象の場合
排反な事象の場合、例えば事象「奇数の目」の下での「偶数の目」の条件付き確率はどうなるでしょうか。
この場合、\( P(奇数の目 \cap 偶数の目) = 0 \)ですので、
\( \hspace{10pt} \displaystyle P(偶数の目 | 奇数の目) = \frac{P(奇数の目 \cap 偶数の目)}{P(奇数の目)} \)
\(\hspace{20pt} \displaystyle = 0 \)
となります。
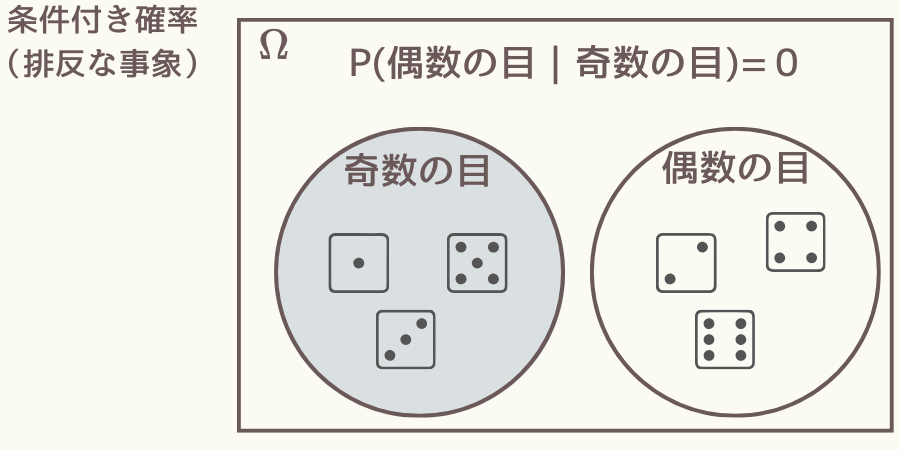
このように排反な事象同士での条件付き確率はゼロになります。
事象Aが起きたら事象Bは起きない、ということですね。
確率の独立性
事象Aと事象Bに次式が成り立つ時、AとBは互いに独立な事象といいます。
\( \hspace{10pt} \displaystyle P(A \cap B) = P(A) P(B)\)
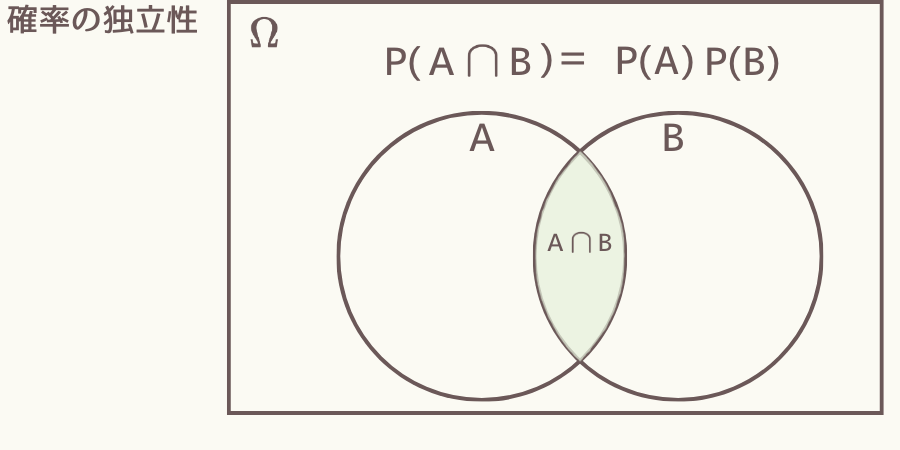
この場合、条件付き確率の式は
\( \hspace{10pt} \displaystyle P(B | A) = \frac{P(A \cap B)}{P(A)} \)
\( \hspace{20pt} \displaystyle = \frac{P(A)P(B)}{P(A)} \)
\( \hspace{20pt} \displaystyle = P(B) \)
となります。
これは事象Bが起きる確率は事象Aが起こるかどうかに無関係であることを意味します。
\( P(A | B) \)も同様に
\( \hspace{10pt} \displaystyle P(A | B) = P(A) \)
となり、事象Aが起きる確率は事象Bが起こるかどうかに無関係です。
つまり、独立な事象同士の場合(\( \displaystyle P(A \cap B) = P(A) P(B) \)が成り立つ場合)、自身の確率は相手の事象が起こるかどうかに無関係です。
また、逆に、お互いに相手が起こるかどうかに無関係である事象同士は独立であり、\( \hspace{10pt} \displaystyle P(A \cap B) = P(A) P(B) \)が成り立ちます。
次に独立性について具体例で見てみましょう。
例えばサイコロ振りの場合、事象「2以下の目」と「奇数の目」のベン図は下図になります。
ただし、各目の出る確率は同じとします。
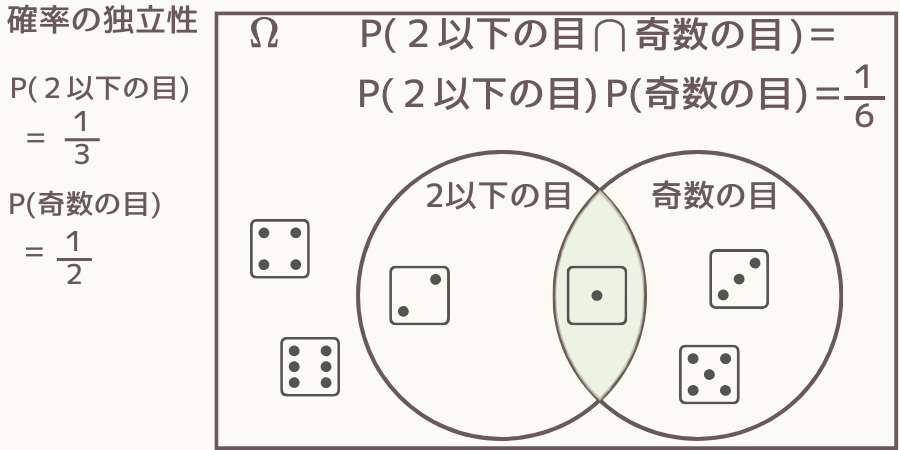
事象「2以下の目」と「奇数の目」の積事象は
\( \hspace{10pt} \displaystyle P(2以下の目 \cap 奇数の目) = \frac{1(5の目)}{6(可能な全ての結果)} \)
であり、それぞれの確率
\( \hspace{10pt} \displaystyle P(2以下の目) = \frac{1}{3} \)
\( \hspace{10pt} \displaystyle P(奇数の目) = \frac{1}{2} \)
から独立性を確認する計算式を計算しても
\( \hspace{10pt} \displaystyle P(2以下の目 \cap 奇数の目) = P(2以下の目) P(奇数の目) \)
\( \hspace{20pt} \displaystyle = \frac{1}{3} \frac{1}{2} = \frac{1}{6}\)
と同じになりますので、互いに独立です。
また、「奇数の目」が起きた場合の「2以下の目」の条件付き確率\( P(「2以下の目」 | 「奇数の目」) \)は
\( \hspace{10pt} \displaystyle P(2以下の目 | 奇数の目) = \frac{P(2以下の目 \cap 奇数の目 )}{P(奇数の目)} \)
\( \hspace{20pt} \displaystyle = \frac{\displaystyle \frac{1}{6}}{\displaystyle \frac{1}{2}} = \frac{1}{3} = P(2以下の目)\)
同様に\( P( 奇数の目|2以下の目 ) \)も
\( \hspace{10pt} \displaystyle P(奇数の目 | 2以下の目) = \frac{P(2以下の目 \cap 奇数の目 )}{P(2以下の目)} \)
\( \hspace{20pt} \displaystyle = \frac{\displaystyle \frac{1}{6}}{\displaystyle \frac{1}{3}} = \frac{1}{2} = P(奇数の目) \)
となり、お互いに相手が起ころうと、起こるまいと確率は変わりません。
排反な事象の場合
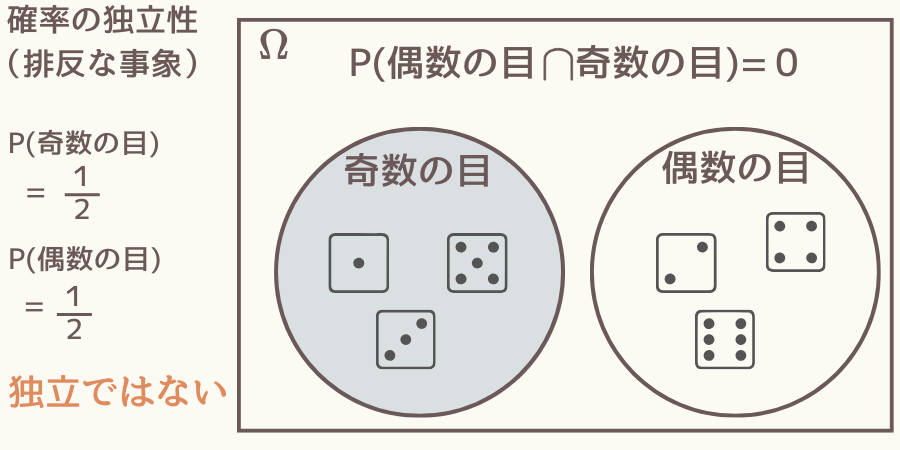
排反な事象の場合、例えば下図のような事象「奇数の目」と「偶数の目」は独立でしょうか。
ベン図を見ると互いに離れているのでなんとなく独立な感じもします。
しかし、よく考えてみると「奇数の目」が出た場合、「偶数の目」の目は出ないことになるので、独立どころか強い関係性があります。
つまり独立ではないのです。
数式でも確認してみましょう。
排反な事象なので積事象は
\( \hspace{10pt} \displaystyle 奇数の目 \cap 偶数の目 = \phi \)
と空事象(含まれる結果一つもない事象)となり、空事象の確率はゼロですので、
\( \hspace{10pt} \displaystyle P(奇数の目 \cap 偶数の目) = 0 \)
となります。
一方、
\( \hspace{10pt} \displaystyle P(奇数の目) = \frac{1}{2} \)
\( \hspace{10pt} \displaystyle P(偶数の目) = \frac{1}{2} \)
ですので、独立性を確認する計算式は
\( \hspace{10pt} \displaystyle P(奇数の目 \cap 偶数の目) = \frac{1}{2}\frac{1}{2} = \frac{1}{4} \)
となり、先程の\( \displaystyle P(奇数の目 \cap 偶数の目) = 0 \)と一致しません。
つまり、独立ではありません。