重ね合わせの原理（電場）

目次（このページで分かること）

重ね合わせの原理（電場）

「電場」のページで、電荷が1個の場合の電場の数式を求めました。

電場

$$ \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\zeta^{2}} \hat{\boldsymbol{\zeta}} $$

電荷が複数ある場合、点$ P $における電場$ \mathbf{E} $はどうなるでしょうか？

重ね合わせの原理（クーロンの法則）では、ソース電荷が複数ある場合の試験電荷に働く力は単純に個々のソース電荷が及ぼす力を足していく事で求めることができました。

電場も同様に重ね合わせの原理を適用できます。

電場の式自体、クーロンの法則から導出されたものなので、当然と言えばそうなのですが。

例えば、$ q_{1} $、$ q_{2} $の二つの電荷が点$ P $に作る電場$ \mathbf{E} $はどうなるでしょうか？

下の動画のように、単純に$ q_{1} $が作る電場$ \mathbf{E}_{1} $と単純に$ q_{2} $が作る電場$ \mathbf{E}_{2} $の和になります。

重ね合わせの原理（クーロンの法則）は次の数式でした。

重ね合わせの原理（クーロンの法則）

$$ \displaystyle \mathbf{F} = \frac{Q}{4 \pi \varepsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\zeta_{i}^{2}} \hat{\boldsymbol{\zeta}}_{i} $$

重ね合わせの原理（電場）においては、上記の数式内の試験電荷である$ Q $を無くすだけです。

重ね合わせの原理（電場）

$$ \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\zeta_{i}^{2}} \hat{\boldsymbol{\zeta}}_{i} $$

ここで、

$ \hspace{10pt} \boldsymbol{\zeta}_{i} = \mathbf{r}-\mathbf{r’}_{i} $

であり、$ \mathbf{r’}_{i} $は電荷$ q_{i} $ の位置ベクトル、$ \mathbf{r} $は点$ P $の位置ベクトルです。

また、電荷$ q_{i} $ の位置ベクトルである$ \mathbf{r’}_{i} $やその電荷量$ q_{i} $は所与の条件（前提として与えられる条件）です。

よって、結局$ \mathbf{E} $ は$ \mathbf{r} $の関数（$ \mathbf{E}(\mathbf{r}) $）になりますので、ご注意ください。

例題

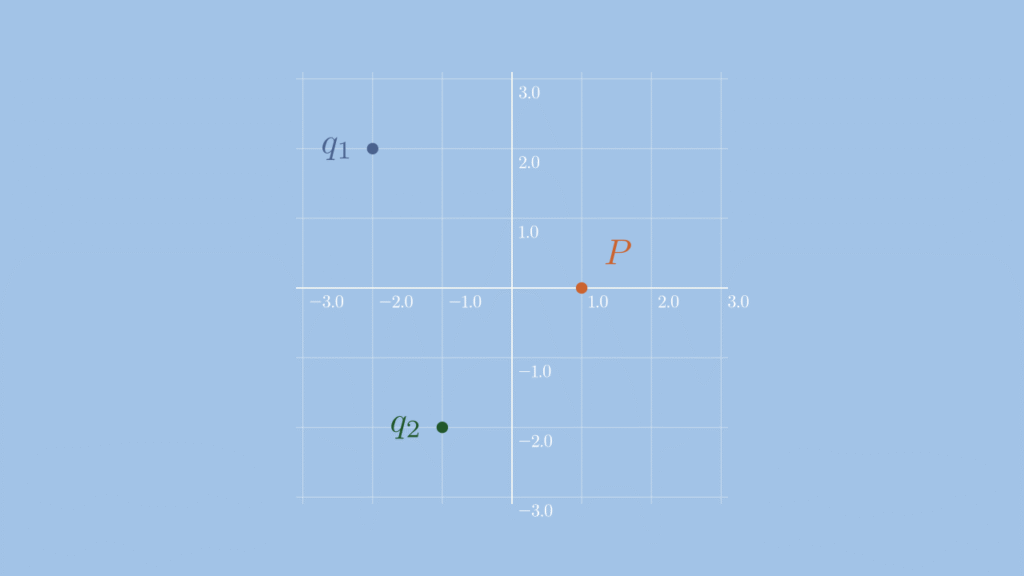
座標$ (-2,2) $の$ q_{1} $、座標$ (-1,-2) $の$ q_{2} $の二つの電荷が座標$ (1,0) $に作る電場$ \mathbf{E} $を計算してください。

重ね合わせの原理（電場）

$$ \displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\zeta_{i}^{2}} \hat{\boldsymbol{\zeta}}_{i} $$

で$ i = 2 $の場合ですので、計算式は次式となります。

$ \hspace{10pt} \displaystyle \mathbf{E} =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{\zeta_{1}^{2}} \hat{\boldsymbol{\zeta}}_{1} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}}{\zeta_{2}^{2}} \hat{\boldsymbol{\zeta}}_{2} $

この中の不明な４つの変数$ \zeta_{1} $、$ \hat{\boldsymbol{\zeta}}_{1} $、$ \zeta_{2} $、$ \hat{\boldsymbol{\zeta}}_{2} $を求めます。

電荷$ q_{1} $の位置ベクトルを$ \mathbf{r’}_{1} $、点$ P $の位置ベクトルを$ \mathbf{r} $とすると、ベクトル$ \boldsymbol{\zeta}_{1} $は$ \mathbf{r’}_{1} $と$ \mathbf{r} $の差ですので、

$ \hspace{10pt} \boldsymbol{\zeta}_{1} = \mathbf{r}-\mathbf{r’}_{1} $

下図のようになります。

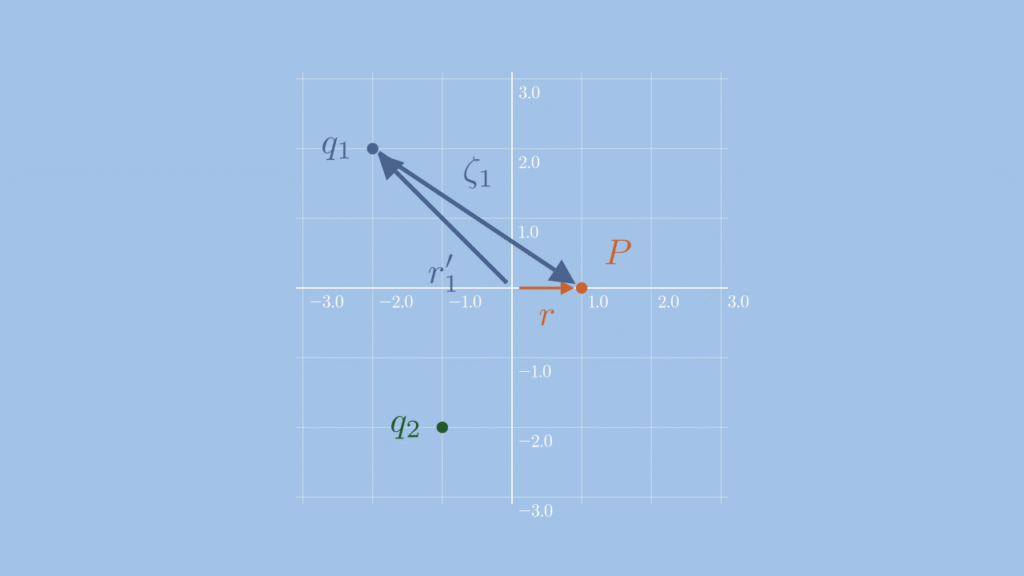
あとはこの$ \boldsymbol{\zeta}_{1} $の大きさ$ \zeta_{1} $と単位ベクトル$ \hat{\boldsymbol{\zeta}}_{1} $を計算することになります。

$ \hspace{10pt} \displaystyle \zeta_{1} = |\mathbf{r}-\mathbf{r’}_{1}| $

$ \hspace{15pt} \displaystyle = |(1 , 0)-(-2,2)| $

$ \hspace{15pt} \displaystyle = |(3 , -2)| = \sqrt{3^{2}+ (-2)^{2}}$

$ \hspace{15pt} \displaystyle = \sqrt{13}$

$ \hspace{10pt} \displaystyle \hat{\boldsymbol{\zeta}}_{1} = \frac{(\mathbf{r}-\mathbf{r’}_{1})}{|\mathbf{r}-\mathbf{r’}_{1}|} $

$ \hspace{15pt} \displaystyle = \frac{(3 , -2)}{\sqrt{13}}$

同様に電荷$ q_{2} $の位置ベクトルを$ \mathbf{r’}_{2} $とすれば、

$ \hspace{10pt} \displaystyle \zeta_{2} = |\mathbf{r}-\mathbf{r’}_{2}| $

$ \hspace{15pt} \displaystyle = |(1 , 0)-(-1,-2)| $

$ \hspace{15pt} \displaystyle = |(2 , 2)| = \sqrt{2^{2}+ 2^{2}}$

$ \hspace{15pt} \displaystyle = 2\sqrt{2}$

$ \hspace{10pt} \displaystyle \hat{\boldsymbol{\zeta}}_{2} = \frac{(\mathbf{r}-\mathbf{r’}_{2})}{|\mathbf{r}-\mathbf{r’}_{2}|} $

$ \hspace{15pt} \displaystyle = \frac{(2 , 2)}{2\sqrt{2}}$

これを代入すれば、電場$ \mathbf{E} $は

$ \hspace{10pt} \displaystyle \mathbf{E} =\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{(\sqrt{13})^{2}} \frac{(3 , -2)}{\sqrt{13}} + \frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}}{(2\sqrt{2})^{2}} \frac{(2 , 2)}{2\sqrt{2}} $

$ \hspace{15pt} \displaystyle =\frac{q_{1}}{4 \pi \varepsilon_{0}} \frac{(3 , -2)}{13\sqrt{13}} + \frac{q_{2}}{4 \pi \varepsilon_{0}} \frac{(2 , 2)}{16\sqrt{2}} $

$ \hspace{15pt} \displaystyle =\frac{1}{4 \pi \varepsilon_{0}} \left( \frac{3q_{1}}{13\sqrt{13}} + \frac{2q_{2}}{16\sqrt{2}}, \hspace{5pt} \frac{-2q_{1}}{13\sqrt{13}} + \frac{2q_{2}}{16\sqrt{2}} \right) $

となります。

電場の例

いくつかの電荷配置パターンにおいて、電場がどうなるか見ていきます。

２つの正の電荷

同じ電荷量の正の電荷を二つ配置した場合の電場の様子です。

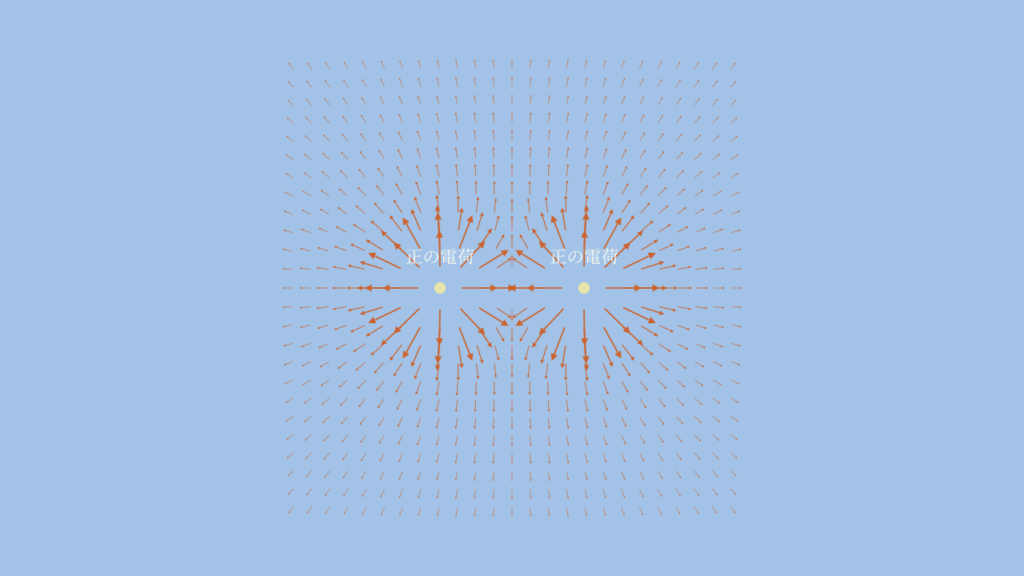
このベクトルをプログラムで流れに変換すると次の動画になります。

正の電荷と負の電荷

同じ大きさの正の電荷と負の電荷を配置した場合の電場です。

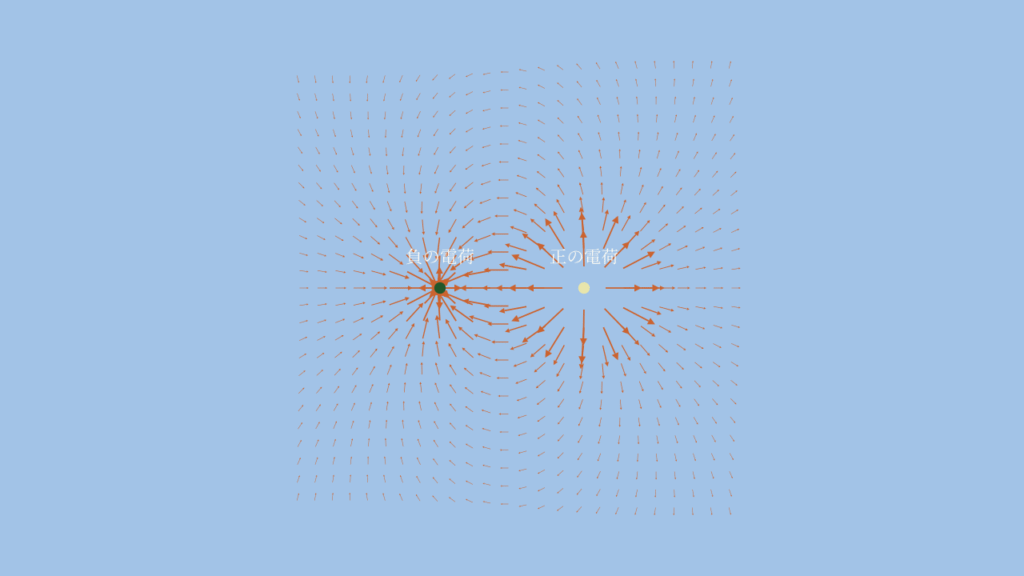
このベクトルをプログラムで流れに変換すると次の動画になります。

時々出てくる長い線はプログラム上の「あや」です。消そうとしてもけせなかったもので・・・