確率とは
確率とは、ある現象が起こる可能性の程度(起こりやすさ)を数値で表したものです。
例えば、サイコロを振った時の1の目の出やすさ、確率:\( 1/6 \)を次のように表現します。
\( \hspace{10pt} \displaystyle P(1の目が出る) = \frac{1}{6} \)
より一般的には、\( A \)が起こる確率は次のように表現します。
\( \hspace{10pt} \displaystyle P(A) \)
ちなみに、\( P \)は英語で確率を意味する「Probability」の頭文字です。
ところで、上のサイコロの例は確率論の説明の際によく使われますが、次のような疑問を感じることはないでしょうか。
「サイコロの1の目が出る確率が\( 1/6 \)というのは、サイコロの6面それぞれが出る可能性が同じと考えた結果だろうけど、本当にそうなの?」
この質問を起点として、いくつかある確率というものの捉え方、考え方を整理したいと思います。
というのも、確率論では確率の捉え方がいくつかあるにもかかわらず、大抵の場合、それを明確にしないまま話を進めます。
そのため場合によっては、このサイコロの例のように前提条件が曖昧な部分が残り、理解の妨げになる可能性があると思われるからです。
質問に戻りますが、実際には、サイコロの各面の出る可能性は異なり、5や6の目が出る確率が高いという実験結果があります。
その理由としては5の面は窪みが5か所あり、対面の2の面は窪みが2か所で、相対的に5の面の方が軽くなり、2の面にサイコロの重心が寄るから、と推察されます。
6の目の場合も同様です。
つまり、確率論の説明においてサイコロはよく出てくる例ですが、そこには各面の出る可能性は同じという暗黙の前提条件(仮定)があります。
確率の定義方法はいくつかありますが、このように確率を定義する方法は古典的定義とよばれます。
古典的定義
「いずれの結果も生じる可能性が同じ場合、確率は注目している結果と可能な全ての結果の比である」
例えば、サイコロの偶数の出る確率は、1~6のいずれの結果も生じる可能性が同じとして、偶数の目が出る確率は
\( \hspace{10pt} \displaystyle P(サイコロの偶数の目が出る) = \frac{注目している結果:2、4、6の3つ}{可能な全ての結果:1~6の6つ} \ = \frac{1}{2} \)
すぐに分かるように、この古典的定義は「いずれの結果も生じる可能性が同じ場合」という限定された状況にしか適用できません。
このような古典的定義の問題に挑戦するものとして登場したのが「統計的(頻度主義的)定義」です。
統計的(頻度主義的)定義
試行(サイコロを振る、実験をするなど)の回数を\( n \)、結果\( A \)が生じた回数を\( n_{A} \)とした場合、確率は次の極限により求められる。
\( \hspace{10pt} \displaystyle P(A) = \lim_{n \to \infty} \frac{n_{A}}{n} \)
例えば、サイコロを振って5の目が出る確率は、ものすごい数サイコロを振った時の「5の目が出た回数」と「サイコロを振った回数」の比であるという考えです。
下図は5000回のサイコロ振りをパソコンでシミュレーションした結果です。
試行回数が増えると一定の値に近づいています。
「古典的定義」と異なり、各目の出る確率が平等に\( 1/6 \)である必要はありません。
ちなみに、上のシミュレーションでは、少し5の目と6の目が出やすくなるように調整しています。
試行の回数を増やせばその確率になる、という上記の定義は直感的にわかりやすく、現実の問題を扱う際に有用な確率の考え方です。
しかし、確率論の数学的な定理などを演繹的に導くための基礎とするには適当ではありませんでした。
現在は次の公理的定義が確率論の基礎として使用されています。
ちなみに、公理とは定理などを演繹的に導く前提条件となるもの、基礎、出発点です。
逆に定理とは公理から演繹的に導かれたものです。
公理的定義
確率は次の3つの公理を満たす必要がある。
- 確率は正の値である。
- 全結果の確率の合計は1である。
- 互いに排反な(同時に生じない)結果のどちらか一方が生じる確率は個々の確率の和である。(例えば、サイコロで3または5の目が出る確率は、3の目が出る確率と5の目が出る確率の和)
確率に関する基本的な事柄しか条件に入っておらず、とても抽象的、つまり適用範囲が広い定義に思われますが、いかがでしょうか。
なお、「古典的定義」は「公理的定義」の特殊なケース(すべての結果の確率が同確率というケース)と言えます。
さらに、「統計的(頻度主義的)定義」も「公理的定義」と矛盾しません。
基本的に確率論は公理的定義を前提としています。
事象とは
大まかに言えば、事象とは試行(サイコロを振ることなど)の結果(1の目が出るなど)を複数集めた集合です。
例えば、サイコロ振りの場合、「奇数の目が出ること」という「事象」は「1の目が出ること」、「3の目が出ること」、「5の目がでること」の3つの結果を集めた集合です。
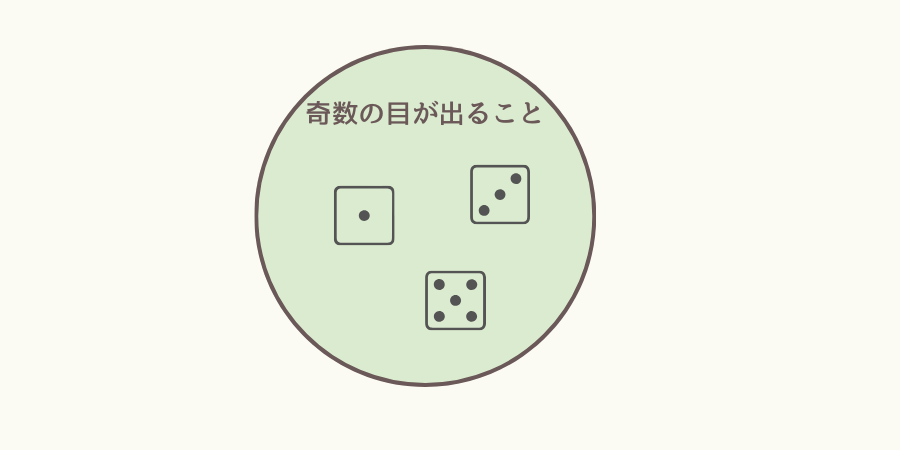
ちなみに、最初に「大まかに」と記載したのは、「1の目が出ること」のように単独の結果や、単独の結果すら含まない場合(結果がない、空の場合)も事象と呼ぶからです。
前者を根元事象、後者を空事象と呼びます。
しかし、「事象」という言葉のメインのイメージとしては、複数の結果を集めた「集合」と捉えた方が、次で説明する和事象や積事象を理解しやすいと思います。
なお、空事象というものがなぜ必要になるのかについては排反事象のところで分かります。
全事象(標本空間)
起こりうる全ての結果のことを全事象また標本空間と呼び、記号\( \Omega \)で表します。
サイコロ振りの例でいえば、出る可能性のあるのは1、2、3、4、5、6の目ですので、全事象(標本空間)は1、2、3、4、5、6の目になります。

通常の事象、例えば「奇数の目がでること」などは全事象(標本空間)の一部になります。

また、このようにして集合を図に表現したものをベン図と呼びます。
和事象
事象A、Bの和事象とは、事象AまたはBの事象のことで、記号で書くと次にになります。
\( \hspace{10pt} \displaystyle A \cup B \)
ベン図で表すと次図になり、和事象の範囲は塗りつぶしの範囲です。

例えばサイコロ振りの場合、事象「奇数の目」と「4以上の目」の和事象は次図になり、和事象は1、3、4、5、6の目です。

積事象
事象A、Bの積事象とは、事象AかつBの事象のことで、記号で書くと次にになります。
\( \hspace{10pt} \displaystyle A \cap B \)
ベン図で表すと次図になり、積事象の範囲は塗りつぶしの範囲です。

例えばサイコロ振りの場合、事象「奇数の目」と「4以上の目」の積事象は次図になり、積事象は5の目だけです。

余事象
事象Aの余事象とは、事象A以外の事象のことで、記号で書くと次にになります。
\( \hspace{10pt} \displaystyle \bar{A} (A^{c}とも書く場合もあります) \)
ベン図で表すと次図になり、余事象の範囲は塗りつぶしの範囲です。

例えばサイコロ振りの場合、事象「奇数の目」の余事象は次図になり、余事象は2、4、6の目です。

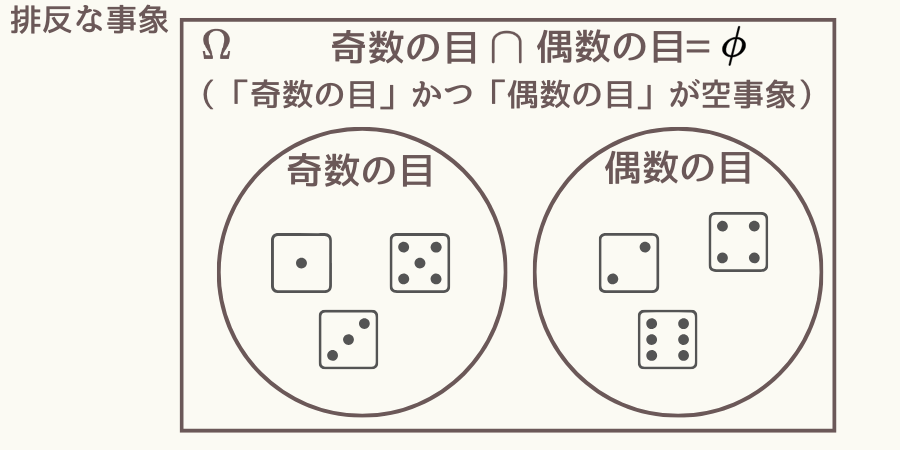
排反事象
事象AとBが同時に生じない場合、事象AとBは排反な事象といいます。
数式で表すと次式の場合、排反となります。
\( \hspace{10pt} \displaystyle A \cap B = \phi \)
\( \phi \)は空事象(含まれる結果が一つもない事象)を表す記号です。
このことから、事象A、Bの積事象が空事象の場合、事象AとBは排反な事象といえます。
ベン図で表すと次図になり、排反な事象同士は共通の結果を持たず、重なる部分がありません。
例えばサイコロ振りの場合、事象「奇数の目」と「偶数の目」は次図のように共通の結果を持たず(重なる部分がなく)、排反な事象です。