ベクトルとは何か?
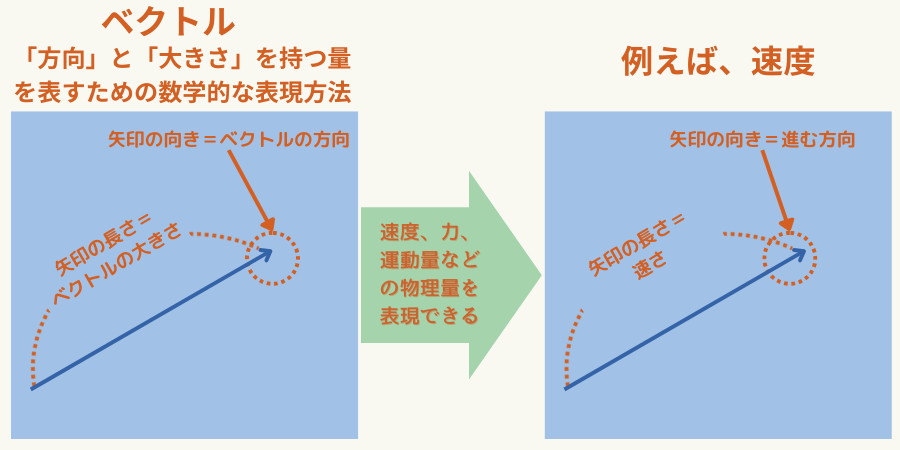
ベクトルとは、「方向」と「大きさ」を持つ量を表すための数学的な表現方法です。
例えば、速度、力、運動量などの物理量を表現するために使用されます。
多くの場合、矢印として表現され、矢印の長さ=大きさ、矢印の向き=方向です。
また、\( \mathbf{a} \)のように太い文字(ボールド)で表されることが多いです。
ベクトルとスカラーの違い
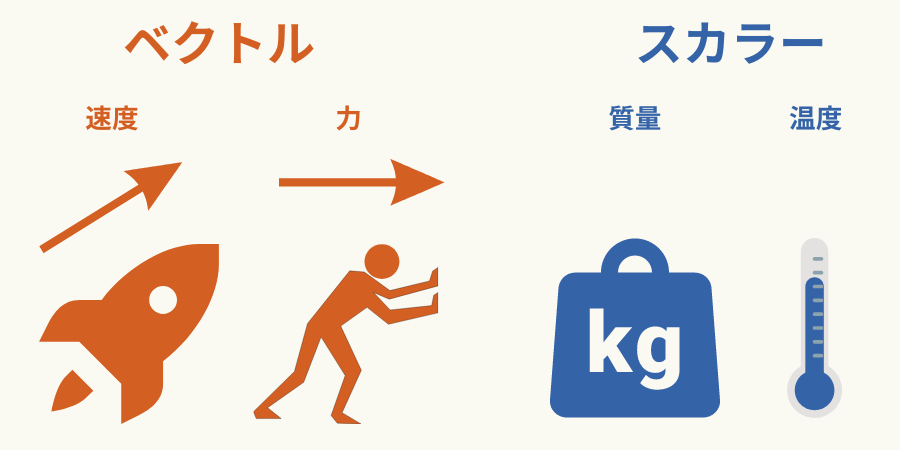
スカラーは、ベクトルと異なり「大きさ」だけを持つ量です。
例えば、質量や温度などの物理量が当てはまります。
ベクトルとは違い向きを持ちません。
スカラーは\( k \)のように、通常の太さの文字で表現されることが多いです。
成分表示
ベクトルの成分表示とは、座標を設定し、その中でベクトルを数値的に表現したものです。
数字で表現することで、ベクトルの数値計算が可能になります。

ベクトル\( \mathbf{a} \)の\( x \)成分は\( 3 \)、\( y \)成分は\( 2 \)であることから、\( \mathbf{a} = (3,2)\)と表現します。
これがベクトルの成分表示です。
通常、ベクトルを扱う場合には、このように座標を設定します。
どのように座標を設定するかは自由ですが、原則として、座標の設定の仕方によってベクトルの値が変わることはありません。
上の図では分かり易くするために、わざと原点をベクトルの始点に合わせましたが、原点と始点が異なる下図のベクトルでも、すべて\( \mathbf{a} = (3,2)\)の同じベクトルになります。
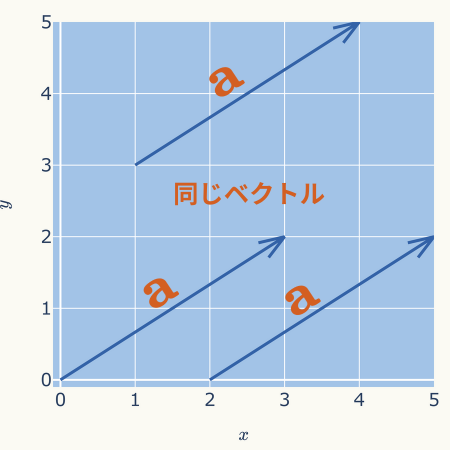
これらは\( x \)方向に3単位、\( y \)方向に2単位移動するので同一のベクトルです。
恣意的に設定される座標の原点位置によって、速度や加速度、力などの値が異なってしまうようでは扱いにくいので、ある意味当然ですね。
ただし、先程「原則として」と書きましたが、例外があり、それは次に説明する「位置ベクトル」です。
位置ベクトル
位置ベクトルは原点を始点としたベクトルであり、成分表示が座標点の値と同じになります。
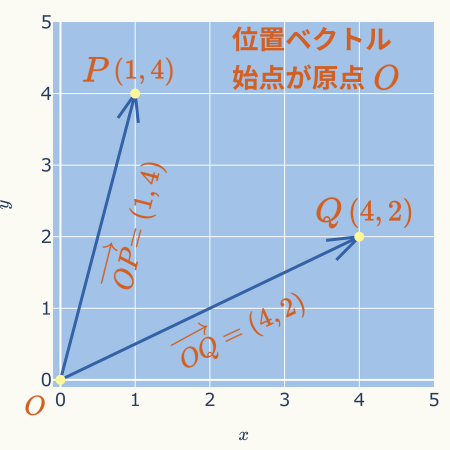
位置ベクトル\( \overrightarrow{OP}=(1,4) \)は座標点\( P(1,4) \)の値と同じになります。
なお、上記のようにベクトルを座標上の点を使って\( \overrightarrow{OP} \)と表すこともあります。
\( \overrightarrow{OP} \)は点\( O \)から点\( P \)に向かうベクトル、という意味です。
位置ベクトルの数値は座標の設定の仕方によって違ってきます。
物理学においては、物体や粒子などのモノの位置を表すのによく使われます。
物体の位置の数字は座標設定によって変わっても、通常、速度や力などの物理量は座標設定の影響を受けないため問題ありません。
また、機械学習においてデータを座標上の点と表すことがよくありますが、これを位置ベクトルとしてとらえ、データが特徴を良く表すように座標軸を設定する手法もあります。
ベクトルの大きさ(ノルム)
ベクトルの大きさ(ノルムとも言います)を\( | \mathbf{a} |\)や\( \| \mathbf{a} \|\)で表します。
\( \mathbf{a} = (a_{1},a_{2}) \)の大きさはピタゴラスの定理より
\( \hspace{10pt} | \mathbf{a} | = \sqrt{a_{1}^{2}+a_{2}^{2}}\)
となります。

例えば、\( \mathbf{a} = (4,3) \)であれば、
\( \hspace{10pt} | \mathbf{a} | = \sqrt{4^{2}+3^{2}} = \sqrt{16+9}\)
\( \hspace{20pt} = \sqrt{25} = 5\)
です。
ベクトル操作
ベクトルのスカラー倍
ベクトル\( \mathbf{a} \)をスカラー倍(\( k \)倍)すると、大きさは\( k \)倍され、向きは\( k \)が正なら同じ向き、\( k \)が負なら逆向きになります。
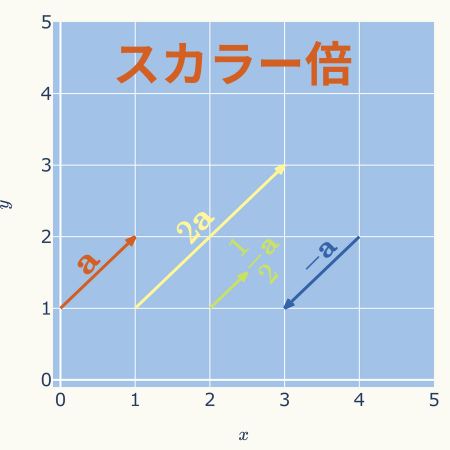
成分表示上の計算は、単に各成分を\( k \)倍するだけです。
\( \hspace{10pt} \displaystyle k \mathbf{a} = k(a_{1},a_{2}) \)
\( \hspace{20pt} \displaystyle = (ka_{1},ka_{2}) \)
例えば、、\( \mathbf{a} = (3,2) \)、\( k=2 \)であれば、
\( \hspace{10pt} \displaystyle 2 \mathbf{a} = 2(3,2) \)
\( \hspace{20pt} \displaystyle = (6,4) \)
となります。
ベクトルの和
和ベクトル\( \mathbf{a}+\mathbf{b} \)は、ベクトル\( \mathbf{a} \)と\( \mathbf{b} \)をつなげた時、始点から終点へ向かうベクトルです。
この動画のように、どちらをどちらにつなげるかは関係なく、同じベクトルを得られます。
また、平行四辺形の形になることも特徴です。
成分表示上の計算は、単に各成分ごとの足し算です。
スマホでご覧の方へ、画面からはみ出るような数式はスクロールできます。
\( \hspace{10pt} \displaystyle \mathbf{a}+\mathbf{b} = (a_{1},a_{2})+(b_{1},b_{2}) = (a_{1}+b_{1},a_{2}+b_{2}) \)
例えば動画のように\( \mathbf{a} = (1,2) \)、\( \mathbf{b} = (3,1) \)であれば、
\( \hspace{10pt} \displaystyle \mathbf{a}+\mathbf{b} = (1,2)+(3,1) = (1+3,2+1) = (4,3) \)
となります。
ベクトルの差
差ベクトル\( \mathbf{b}-\mathbf{a} \)は、\( \mathbf{b}+(-\mathbf{a}) \)と見なせるので、ベクトルの和と同じ要領で計算できます。
動画にあるように、結局、差ベクトル\( \mathbf{b}-\mathbf{a} \)は\( \mathbf{a} \)の終点から\( \mathbf{b} \)の終点に向かうベクトルになります。
これは\( \mathbf{a} \)と\( \mathbf{b}-\mathbf{a} \)の和が\( \mathbf{a}+(\mathbf{b}-\mathbf{a})= \mathbf{b}\)となることから証明されます。
成分表示上の計算は、単に各成分ごとの引き算です。
\( \hspace{10pt} \displaystyle \mathbf{b}-\mathbf{a} = (b_{1},b_{2})-(a_{1},a_{2}) = (b_{1}-a_{1},b_{2}-a_{2}) \)
例えば動画のように\( \mathbf{a} = (1,2) \)、\( \mathbf{b} = (3,1) \)であれば、
\( \hspace{10pt} \displaystyle \mathbf{b}-\mathbf{a} = (3,1)-(1,2) = (3-1,1-2) = (2,-1) \)
となります。
その他のベクトル操作
その他にベクトルの内積(スカラー積)、外積(ベクトル積)があります。
位置ベクトルを使用した点間距離の計算
位置ベクトルの差を使って、下図のように点間の距離を求める事ができます。

上の図の場合、\( \boldsymbol{p} = (1,4) \)、\( \boldsymbol{q} = (4,2) \)ですので、
\( \hspace{10pt} \displaystyle \boldsymbol{q}-\boldsymbol{p} = (4,2)-(1,4) = (4-1,2-4) = (3,-2) \)
となります。
よって、点PQ間の距離は
\( \hspace{10pt} | \boldsymbol{q} – \boldsymbol{p} | = \sqrt{3^{2}+(-2)^{2}} = \sqrt{9+4} = \sqrt{13}\)
です。
単位ベクトル
単位ベクトルとは、大きさ1のベクトルです。
ベクトルは自身の大きさ(ノルム)で割ることにより、同一方向の単位ベクトルになります。
\( \hspace{10pt} \displaystyle \hat{ \mathbf{a}} = \frac{ \mathbf{a} }{| \mathbf{a} |} \)
\( \hat{ \mathbf{a}}\)は\( \mathbf{a} \)ハットと読み、単位ベクトルの表現としてよく使われます。
例えば、\( \mathbf{a} = (4,3) \)であれば、
\( \hspace{10pt} \displaystyle \hat{ \mathbf{a}} = \frac{(4,3)}{5} \)
\( \hspace{20pt} \displaystyle = \left( \frac{4}{5},\frac{3}{5} \right) \)
です。
基底ベクトル
基底ベクトルとは、座標軸の正の方向を向き、大きさが1のベクトル(単位ベクトル)です。
\( \mathbf{i}\)、\( \mathbf{j}\)、\( \mathbf{k}\)や\( \hat{ \mathbf{x}}\)、\( \hat{ \mathbf{y}}\)、\( \hat{ \mathbf{z}}\)や\( \boldsymbol{e}_{1}、\boldsymbol{e}_{2}、\boldsymbol{e}_{3} \)などで表します。
\( \hspace{10pt} \displaystyle \mathbf{i} = \hat{ \mathbf{x}} = \boldsymbol{e}_{1} = (1,0)\)
\( \hspace{10pt} \displaystyle \mathbf{j} = \hat{\mathbf{y}} = \boldsymbol{e}_{2}= (0,1)\)
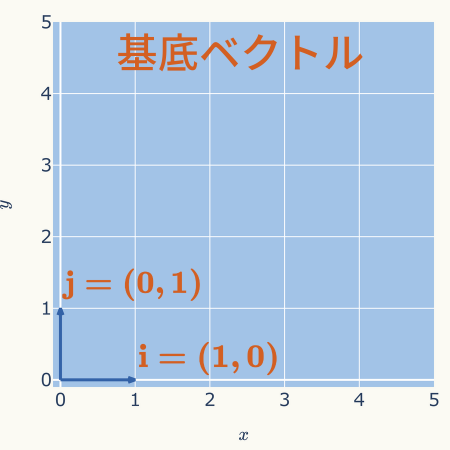
これら基底ベクトルを使用して、成分表示することもよくあります。
\( \hspace{10pt} \displaystyle \mathbf{a} = (a_{1},a_{2}) = a_{1}\mathbf{i}+a_{2}\mathbf{j}\)
\( \hspace{10pt} \displaystyle \mathbf{a} = (3,2) = 3\mathbf{i}+2\mathbf{j}\)
ちなみに、3次元は
\( \hspace{10pt} \displaystyle \mathbf{i} = \hat{\mathbf{x}} = \boldsymbol{e}_{1}= (1,0,0)\)
\( \hspace{10pt} \displaystyle \mathbf{j} = \hat{\mathbf{y} }= \boldsymbol{e}_{2}= (0,1,0)\)
\( \hspace{10pt} \displaystyle \mathbf{k} = \hat{\mathbf{z} }= \boldsymbol{e}_{3}= (0,0,1)\)
となります。
